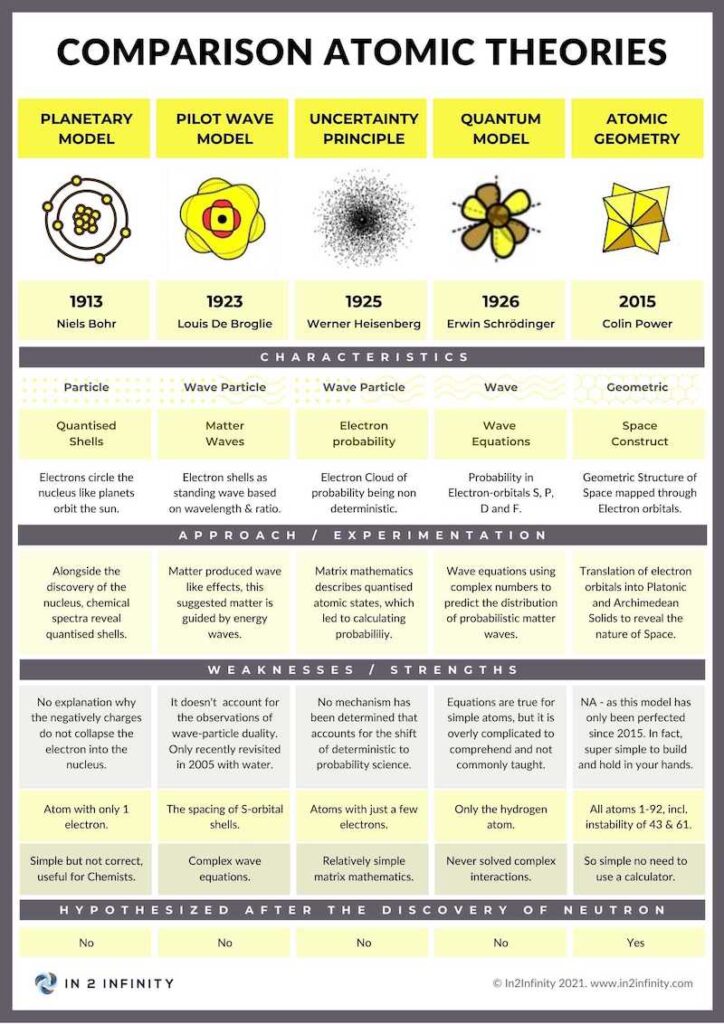
Atomic geometry is the world’s first comprehensive geometric model of the atom, that visualises the electron cloud through three-dimensional polyhedra. Whereas other models describe the atom from the perspective of energy, this one observes the geometric patterns of space generated by the 4 types of Orbital S, P, D and F.
Drawing inspiration from Schrödinger’s wave equations, we find the electrons fall into distinct geometric arrangements, which can be translated directly into Platonic and Archimedean Solids. These are nested perfectly inside each other to produce a 3D representation of all the stable elements on the Periodic table.

Overview
Image you could hold a 3D model of an atom in your hands. Well, now you can! Atomic Geometry maps the S, P, D and F electron orbital using simple 3D geometry. Each of the polyhedra exhibits a specific side-length, that allows them to be nest inside each other, just like Russian dolls. This result accurately reflects the spatial arrangement of the electron cloud, which produces a model that is over 100% more accurate than the Bohr model, and vastly simpler to understand than quantum field theory.
This structure leads to a new theory of the atom, which unifies the proton and electron as a single 4th dimensional entity. Using the mathematics of 4D polytopes, we are able to solve the paradoxes presented by present quantum theory. Atomic Geometry is the first theory of the atom that can explain the stability of electron cloud, and define the exact mechanism by which electrons can jump from one shell to another without appearing in the space between shells. It also resolves the wave-particle paradox, of the electron, without the need of probability theory.
This tactile exploration of the atom is offers a fantastic educational tool for students to comprehend the depths of atomic theory. Children as young as seven years of age are able to recognise complex ideas such as the electron configuration, orbital shells S, P, D and F, the atomic nucleus, and electron pairing. Atomic geometry is the only model of the atom that can be created using a drawing compass, ruler, card, scissors, and glue.
Watch the Video
To gain a clearer overview of Atomic Geometry, its principles and explanations, we have created a short animation video that shows how the four different orbital types combine to form an interlocking structure, based on Platonic and Archimedean Solids.
Key Points
-
Atomic geometry is the world 1st completely geometric model of the atom.
-
S, P , D and F orbitals are 2D shapes a represented as the dot, line, square, and hexagon
-
Orbitals combine to form geometries that can be represented as a nested set of Platonic and Archimedean Solids
THE
Concept
A Geometric perspective of the Atom
With Atomic Geometry we offer a completely new perspective of the atom, which was developed in 2015 by Colin Power, co-founder of In2Infinity. The inspiration for this model came from his in-depth exploration of compass construction. Indeed, throughout the history of humanity, this drawing technique has revealed many scientific laws and discoveries. From the ancient world of Plato and Pythagoras, Euclid’s ‘The Elements’, to great thinkers such as Leonard Da Vinci, and astronomers such as Johannes Kepler, all have employed the drawing compass in their exploration of the universe.
For the first time, we have applied these geometric techniques to the structure of the electron cloud. This journey of has brought many surprises that have revolutionised our perception of the atom, and provides new answers to the mysteries of the quantum world.
A New Geometric Model
of the atom
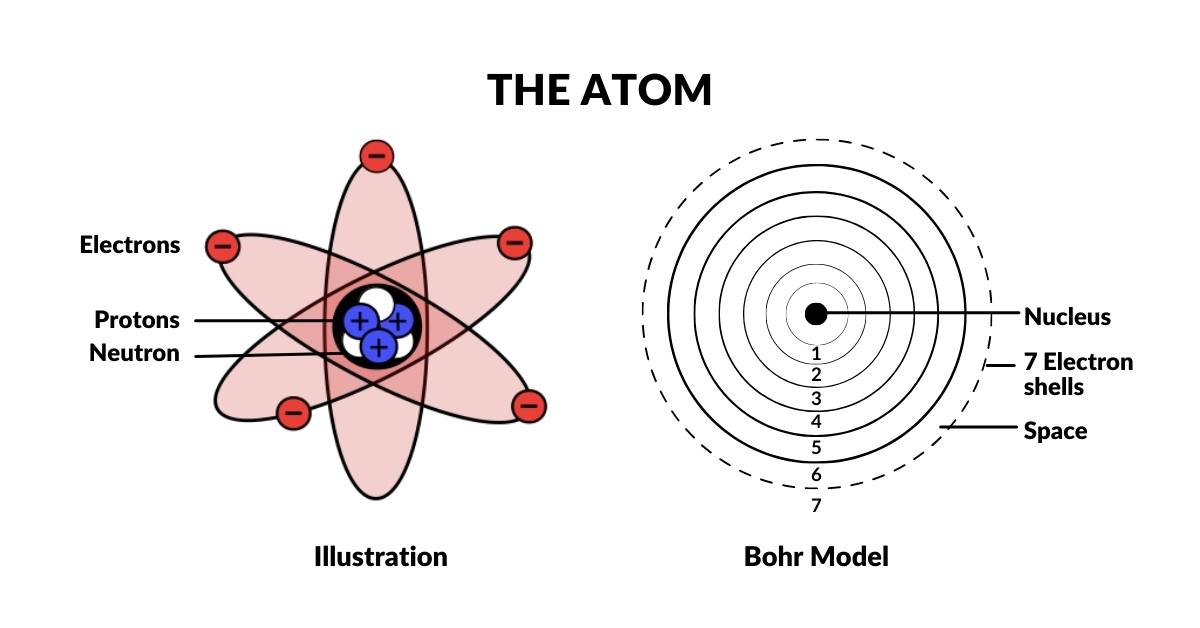
The Atom
The Electron Cloud
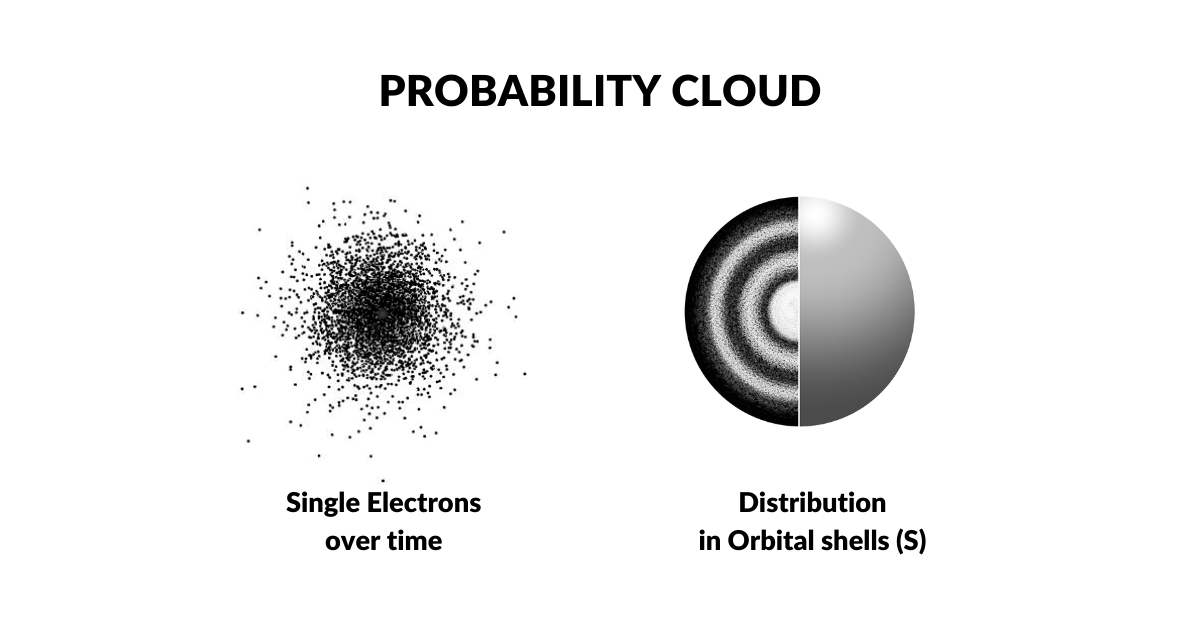
The Bohr Model was disproven in the 1920s when Louis de Broglie discovered that electrons exhibit wave-like characteristics. This led Werner Heisenberg to the hypothesis that electrons exist as a wave of probability. This notion was supported by the fact that the exact location of the electron defied measurement. As both light and electrons seemed to exhibited wave-particle phenomena, it was concluded that the act of measurement (observation) itself collapses the wave into a single particle. This established the electron cloud as a function of probability, which is the prevailing model of today, called the Copenhagen Interpretation. Extensions of this theory conclude that the electron has the possibility of appearing anywhere in the universe. Yet, the exact mechanism that accounts for this still remains an unsolved mystery.
The idea that electrons are not particles has never been entertained by the scientific community. As light was supposed to exhibit a wave-particle duality, so the assumption is that the same premise applies to the matter itself. However, our new solution to the Ultraviolet Catastrophe, and Photoelectric effect, demonstrates that the particle photon suggested by Albert Einstein is not required. Instead, both of these problems can be resolved with a wave model.
Explore the wave solution to the photon
When we apply the same notion to the electron cloud, it ceases to become a particle, and now acts like a 4D field of energy. This solution solves many of the paradoxes in quantum theory, including the reason the radius of the electron has defied definition. This means that we are able to discard the notion of probability and place greater importance on the geometry of the electron cloud itself.
find out more about the 4D nature of the electron cloud
A geometric perspective
Thus far, all models of the atom have been created by gathering data through energetic means using alpha, beta and gamma rays. This has resulted in the discovery of sub-orbital shells with specific configurations. It is this spatial arrangement which creates the characteristics of compounds and molecules within the discipline of molecular geometry. However, so far, the underlying principles have never been explored from the perspective of geometry in any detail. Yet when we do, we find the results are quite surprising.
Atomic Geometry represents the sub-orbitals using simple 2D and 3D geometry. By doing so, it reveals that the electron cloud is highly geometric. Additionally, this notion is extended in the field of Geoquantum Mechanics to model dynamic pathways, whereby energy can be quantised via certain geometric processes. From this perspective, we can explain why electron cloud is quantised at specific energy levels, and why the atomic structure is extraordinarily stable. So far, these questions are still unsolved by traditional quantum theory.
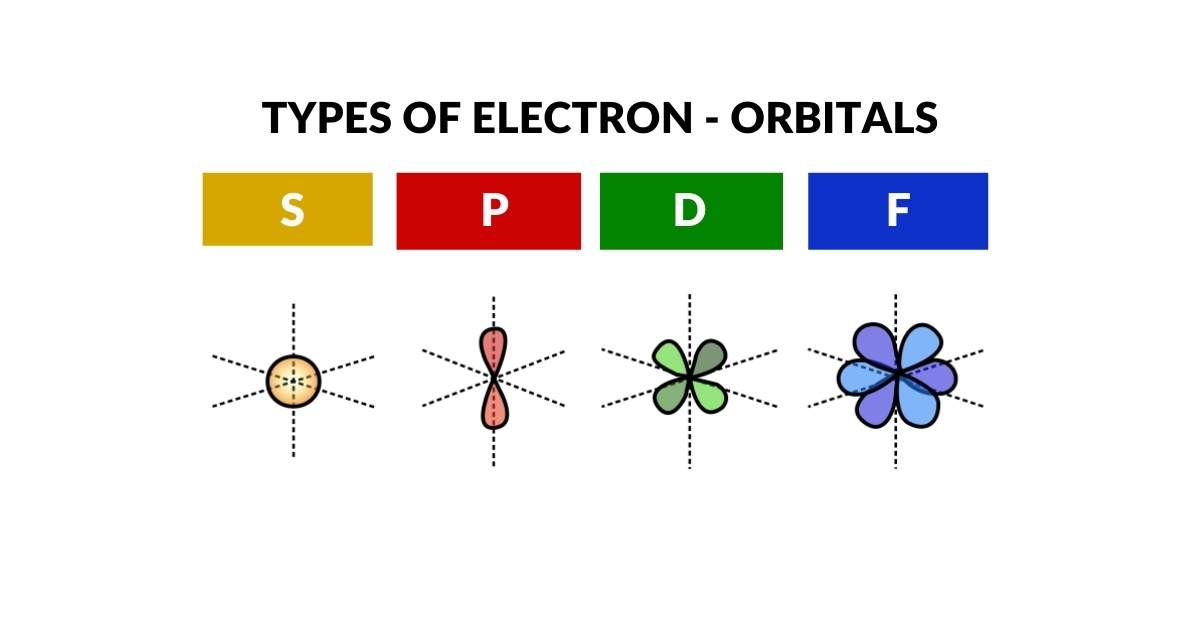
Electron Orbitals
The S, P, D and F-orbitals of the electron cloud define precise spaces around the nucleus where electrons can appear with the ‘highest probability’. Current theories of Quantum Wave Mechanics have noted the relationship of these orbital formations to spherical harmonics. Despite consistent experimental evidence, this phenomenon lacks a clear conclusion.
Electron Configuation
When we study the electron cloud, it reveals that sub-orbitals appear in a specific order and number. This is termed the ‘Electron Configuration‘.
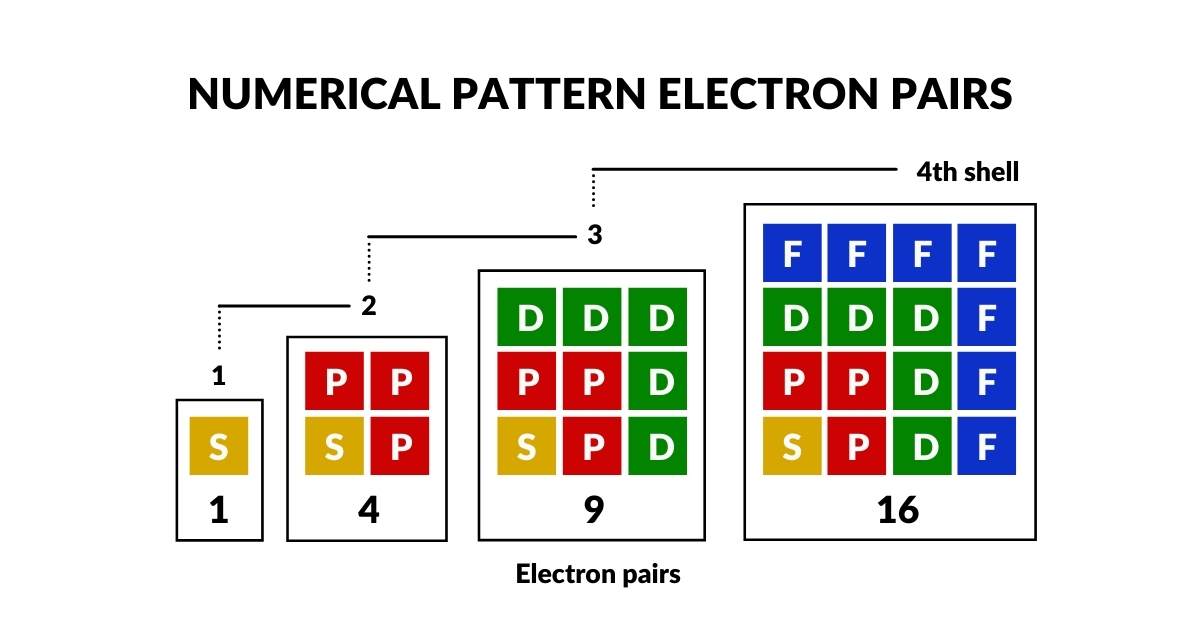
The first is the S-orbital, which appears once in each shell. Subsequently, P-orbitals appear in sets of 3, D-orbitals in sets of 5, and F-orbitals in sets of 7. It is interesting to note that the number 7 also appears to be the limitation for the maximum number of shells up to Uranium (92), the last naturally radioactive element.
The expanding numerical pattern of the orbitals of 1, 3, 5 and 7 is an odd number series, which conveniently falls into a triangular formation – our first geometric insight into the atomic structure. More geometry becomes apparent when we detail the orbitals within each sub-shell. When adding up all orbital pairs per shell, it exposes a numerical pattern from 1, 4, 9 and finally 16. 16 is the maximum number of electron pairs that can be found in a single shell.
This construct of 1, 4, 9, and 16 can be created from a square number series, i.e. 1², 2², 3² and 4². Before examining the geometry of the orbital types themselves, it already becomes clear that there is a numerical mechanism at play which limits the nature of the electron cloud. The combination of odd numbers 1-7, are compounded with each new shell, to generate square numbers which relate to the number of electrons.
Key point
The electron cloud is structured through a combination of odd numbers 1-7, that are compounded with each new shell, to generate square numbers series.
- N = 1, 2, 3, 4, 5, 6, 7 = shell (energy level)
- L = 0, 1, 2, 3 = orbital type (sub-shell, 0 = S, 1 = P, 2 = D, 3 = F,)
- M (L) = – L…L (type of orbital L, i.e. 1S, 3P, 5S, 7F / electron pair)
- M (S) = +1/2 or -1/2 (spin of electron within electron pair)
2D orbital geometry
Find out more about 2d orbital geometry
3D orbital geometry
Having unified the sub-orbital types with geometric laws of the second dimension, it is not surprising that this extends into 3D. Each sub-orbital comprises a specific number to form a complete three-dimensional set. Once the shape is filled, electrons will jump to the next shell of the atom. In the next part, we will consider these formations from the perspective of 3D.
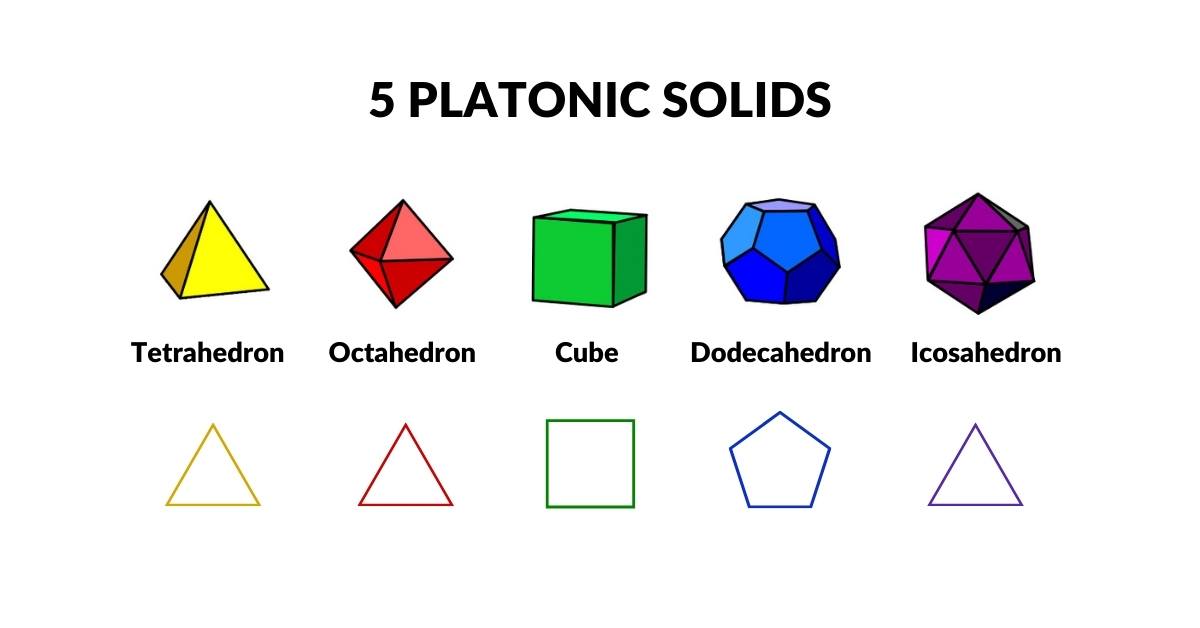
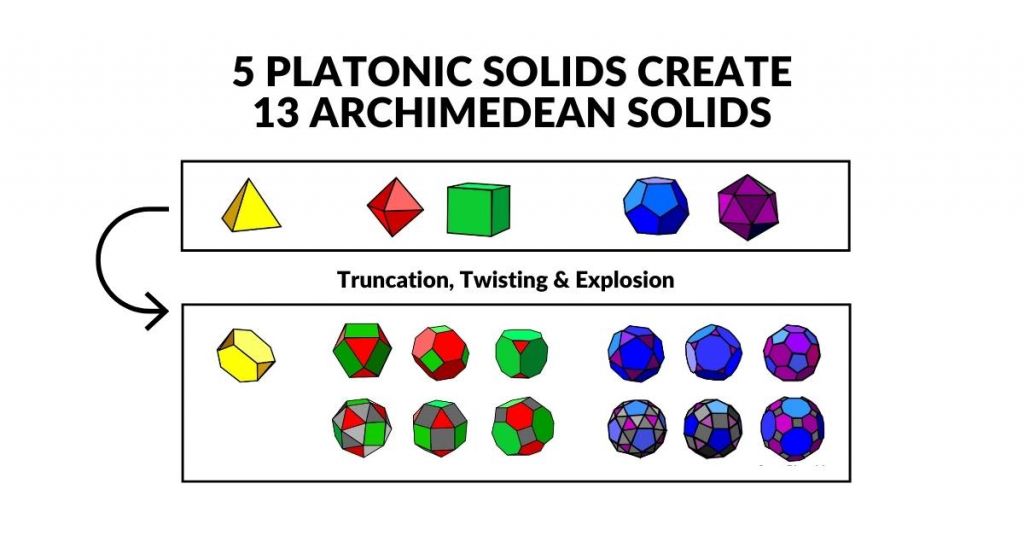
The 5 Platonic and 13 Archimedean Solids
Atomic Geometry produces a 3D model of the S, P, D, and F orbitals using the regular and semiregular solids.
Just as 2D space comprised of just two colours is limited to only two types of regular polygons, the square, and triangle, 3D space is limited to only five regular polyhedra. These are called ‘Platonic Solids’. They are unique, as they are all made from the same regular sided polygons. This means all edges have the same length and all corners have the same distance to the centre.
Three of these, the Tetrahedron, Octahedron, and Icosahedron, have triangular faces. The Cube has square faces, and the Dodecahedron is pentagonal.
The five Platonic Solids can be transformed into a set of 13 semiregular polyhedra, called the Archimedean Solids, through the process of truncation, explosion, and twisting. Aside from the Truncated Tetrahedron, the other 12 fall into two distinct categories. Six are based on the Octahedron and Cube with octahedral symmetry, and another six are derived from the Dodecahedron and Icosahedron with icosahedral symmetry.
If you are not familiar with these forms, you can explore them in great detail in our Guide to Sacred Geometry.
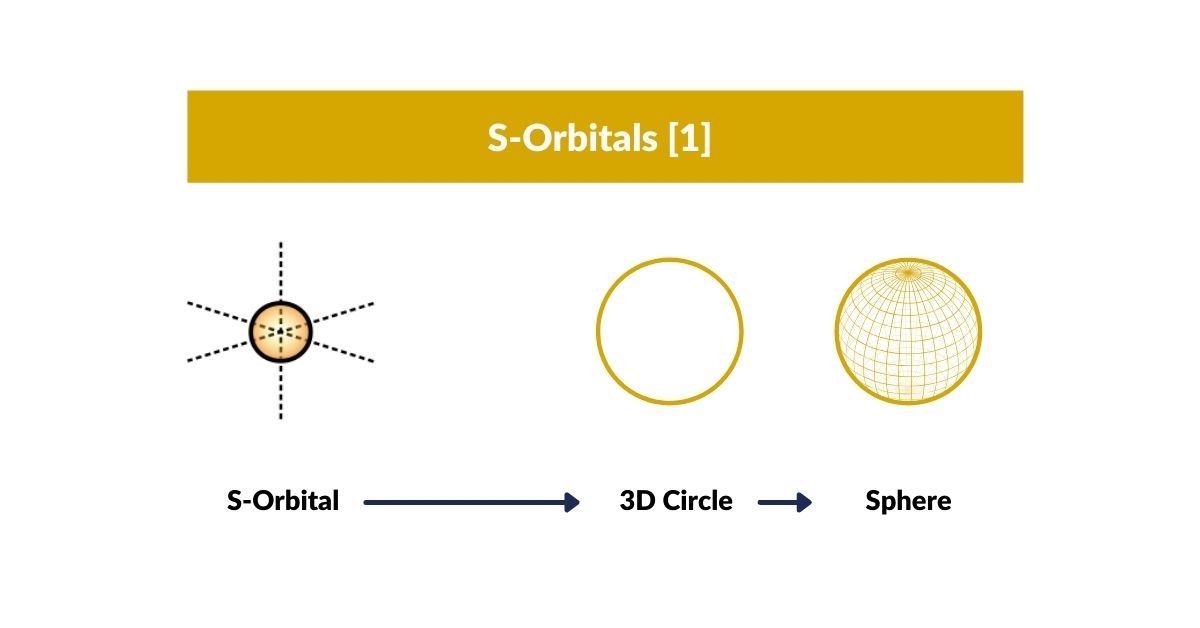
S-Orbitals
S-Orbitals and the Torus
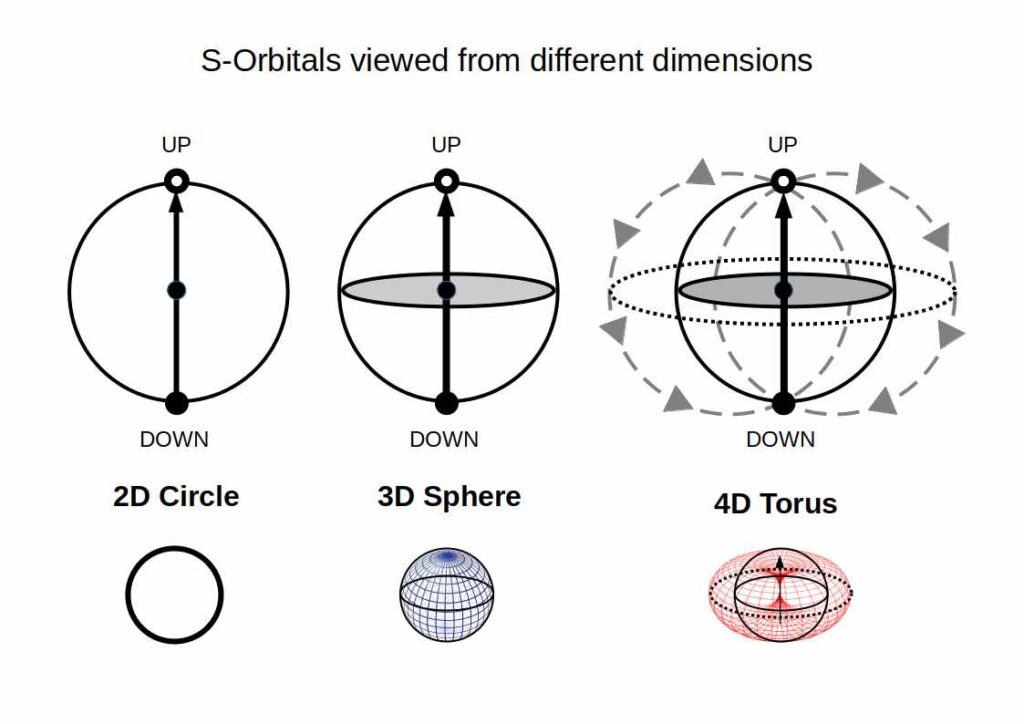
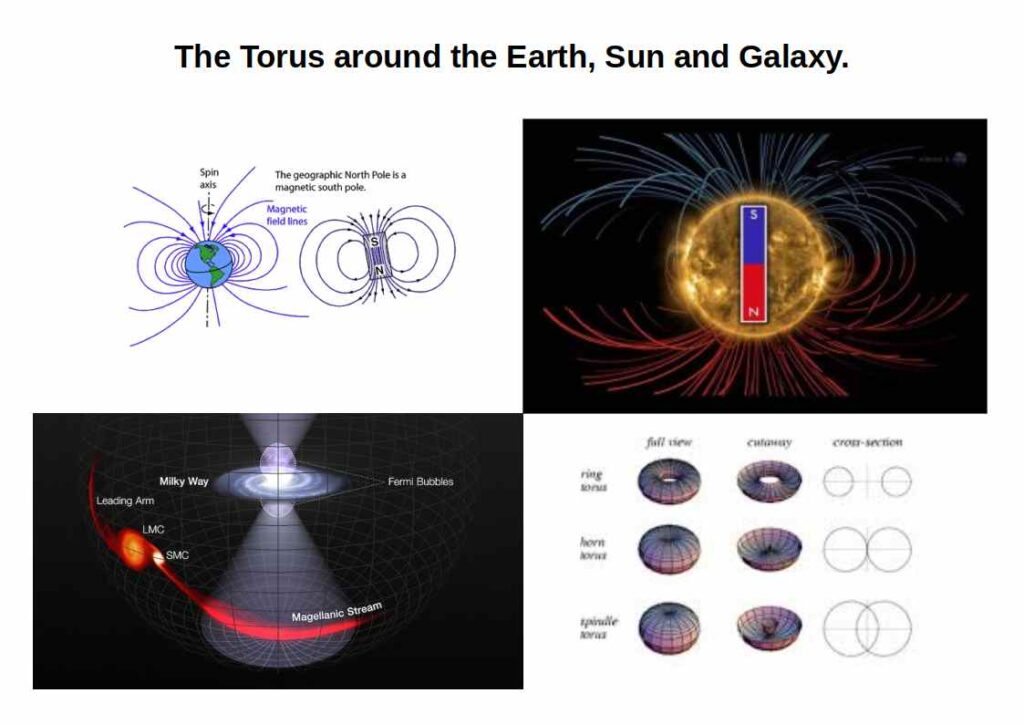
We can perceive S-orbitals from the perspective of a circle (2D), sphere (3D), or torus (4D). The circle is a shadow projection of a 3D sphere onto a 2D space, the sphere a 3D representation of a 4D torus. Let’s go through each dimension and how it relates to the electron pair.
In 2D, the two electrons appear opposite each other on the endpoints of the circle’s diameter, which refers to the up and down configuration. On a 3D sphere, these electrons will be exactly opposite on its surface, which represents the traditional view of particle physics. In a 4D torus, the electrons are still opposite but follow the flow of the field, explaining the up and down orientation.
The 4D torus is a dynamic field, which is in continuous motion and typically represents electromagnetic fields, who exhibit a North and South Pole. Within these torus fields, there is a unidirectional flow of energy, going up and down. We can represent this by simply drawing an arrow that stretches from the ‘down’ orientated electron, to pass through the centre (nucleus) and reach the ‘up’ orientated electron. The arrow represents the flow of energy through the centre of a toroidal structure.
In light of these different dimensions, we propose that the electron spin and the existence of electron pairs are a consequence of a 4D toroidal dynamic. As our perception of reality is limited to 3D, 4D phenomena do not appear to us as physical objects, but rather as electromagnetic fields found around planets, and solar systems. We also suggest that they exist around each galaxy. In fact, they seem to exist on every scale, a realisation far deeper than it may first appear.
The holy grail of quantum physics is to unify quantum gravity, the quantised phenomena of the micro scale, with the theory of general relativity, the smooth curvature of time-space at the macro scale. Could 4D geometry help us resolve this conundrum? We believe that the answers lies within geometry, which we have started to outline in Atomic Geometry and will reveal in more detail in our other ideas and theories.
Find out more about S-orbital geometry
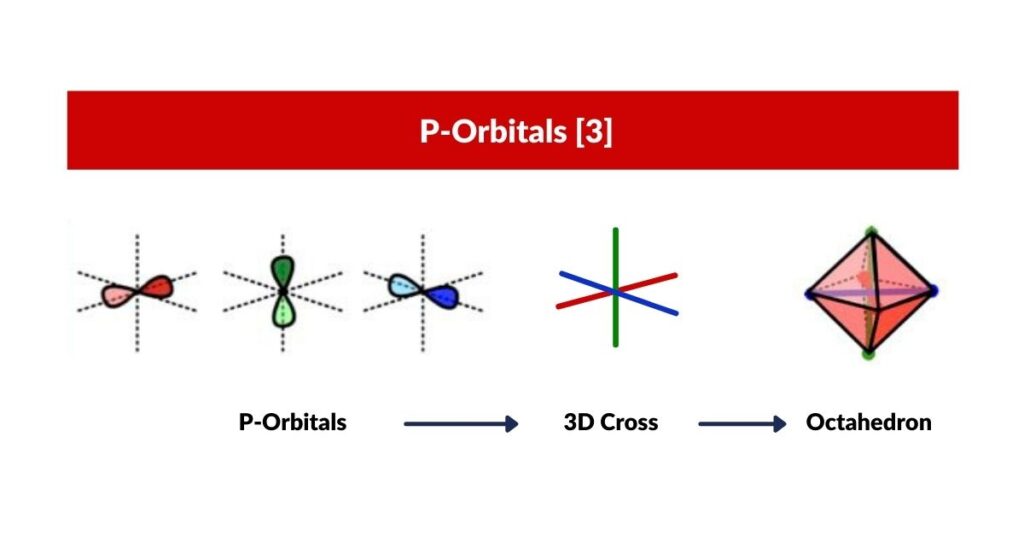
P-Orbitals
P-Orbitals and the Octahedron
Key point
The set of p-orbitals is 3 interlocking torus fields, mapped onto an Octahedron.
4th Dimensional P-Orbitals
To conclude, we have suggested that S-orbitals are 4D in nature, which explains why electrons fall into pairs. Extending this to the P-orbitals, we find that each lobe is constructed by the intersection of two torus fields positioned at 90°to each other.
Watch the Video
In this Video Dr. Heike Bielek demonstrates the Octahedral nature of the P-orbitals,
Find out more about p-orbital geometry
D-Orbitals
The first D-orbitals appear in the 3rd shell of the atom, between the S and P-orbitals. This is not obvious when we look at the traditional periodic table, where the D-block begins in the 4th row (shell). This is because the elements are laid out in terms of their increase in energy levels.
If we analyse it in terms of space, the arrangement would look quite different. After the noble gas argon (18), the next two electrons produce an S-orbital in the 4th shell. Subsequently, the first set of D-orbitals appear in the 3rd shell. Therefore, all D-orbital elements have two S-orbital electrons that can form bonds independently (exceptions to this are the elements that define the Aufbau Principle).
This is why D-orbital element can create such a wide variety of metal alloys. They can form molecular configurations independently of their S-orbitals that appear in the shell above. Most of these metals can be oxidised, when a free oxygen atom forms a bond with the outer S-orbitals, producing the phenomena we call rust.
Another important fact is that there are only three sets of D-orbitals that are comprised of stable atoms. The fourth set (elements 103-112) are highly radioactive, and do not appear in nature. They can only be manufactured within the lab, and tend to exist for just a fraction of a second. No element beyond 100 has ever been synthesised in any kind of macroscopic quantity observable by the human eye.

Therefore, only 3 sets of D-orbital electrons form stable atoms, which appear in the 3rd, 4th, and 5th shell. This suggests that the atom does not expand uniformly, rather, with each successive shell, the next type of orbital appears. This pattern continues up until the F-orbitals in the 4th shell. After this, successive shells have one less stable orbital type.
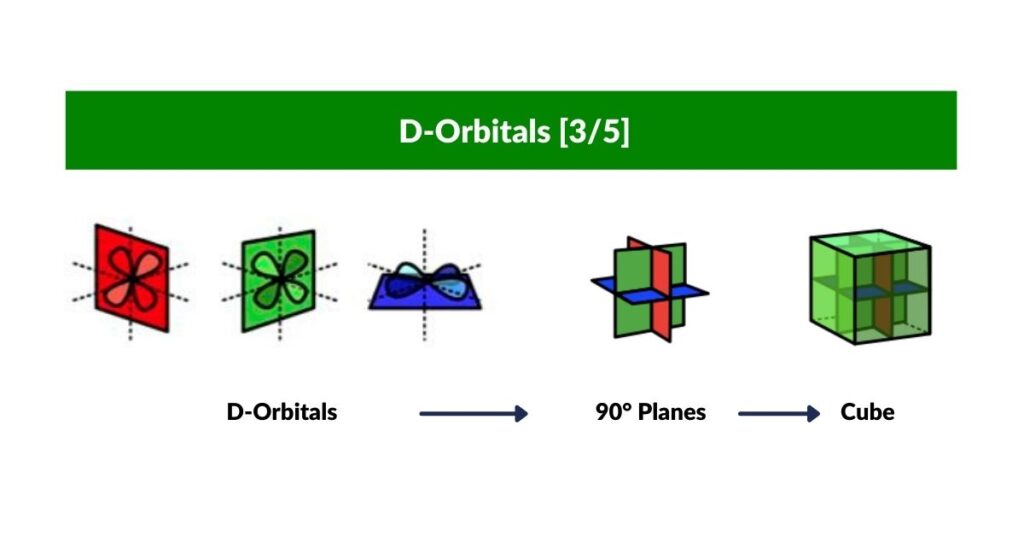
D-Orbitals and the Cube
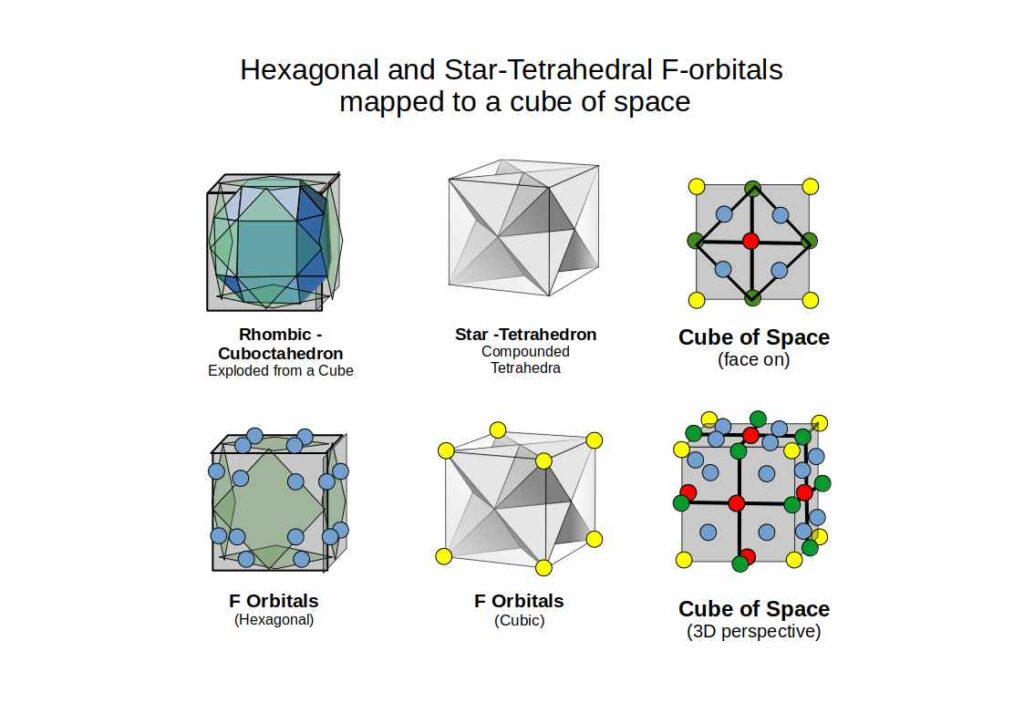
Out of the five D-orbitals, three fall upon the same x, y, z axis as the previous set of P-Orbitals. Each lobe of these ‘cross’ shaped orbitals are located above and below the existing P-orbital. Viewed like this, the D-orbitals are derived from the division of a P-orbital (line) into a cross (two intersecting lines). A simple process of division.
When these D-orbitals are combined they divide a Cube of empty space into eight parts. We can model this geometrically as set of eight small Cubes, complied to form a larger Cube.
Atomic Duals and notions of space
In the Geometric Universe theory, there are different types of space, which are defined by the geometric form that produces each one. The term ‘cubic space’, relates to the spacial dimension associated with the cube. Thus, it has distinctly different qualities to ‘octahedral space’ which tends to leave tetrahedral spaces. The Cube is unique amongst the set of the Platonic Solids, as it is the only form that can fill space uniformly by itself. This space-filling property is descriptive of the space that we experience in daily life.
Objects are orientated in space, and can move through space without changing shape or dimension. Cubic space, as a uniform structure, is the only regular solid that can fulfil this function. Through such a uniform matrix, relative distances in space can be metered and measured.
Based on the foundations of the octahedron, which embodies both triangle and square planes, its Platonic dual, the cube can form. The geometric pattern of the ‘matrix of space’ is perfectly described through the order and appearance of the electron orbital types.
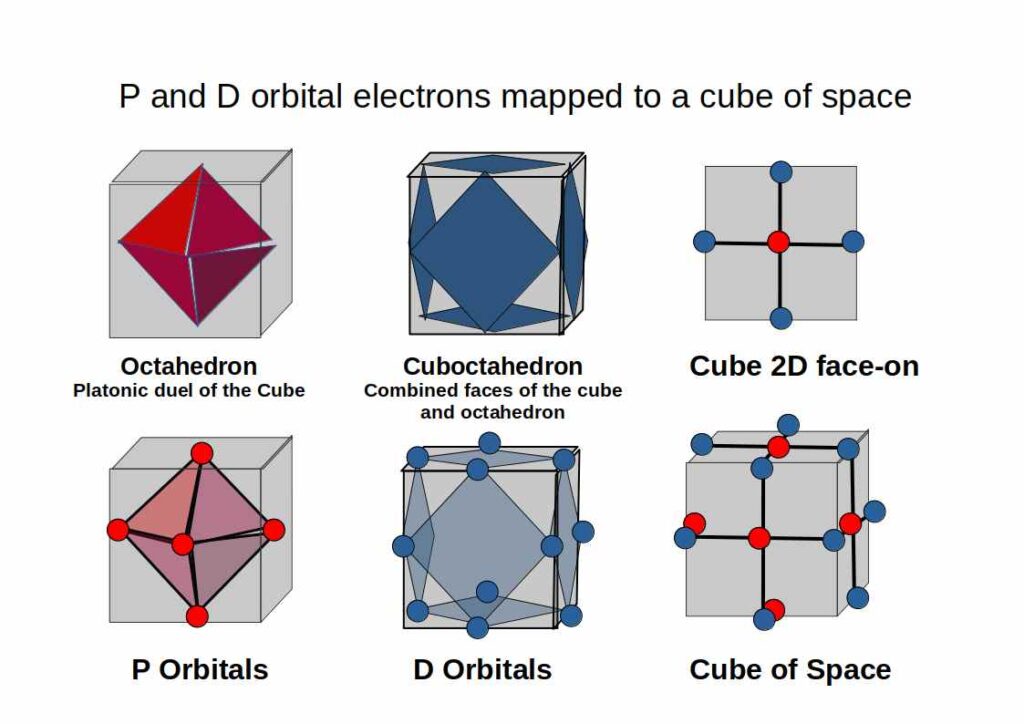
D-orbitals and the Cuboctahedron
Let us next consider the spacial arrangement of a combined set of P and D-orbitals. To help us we can imagine a Cube of empty space. An Octahedron can be placed inside of a Cube in such a way that its 6 corners touch the centre of each face of the Cube. This is because the Cube and Octahedron are ‘Platonic Duals’. The Cube has 6 faces and the 8 corners, the Octahedron has 6 corners and 8 faces.
If we consider the position of the three D-orbitals, we find that they fall on the centre of each square. By connecting the set, a new form appears, the Cuboctahedron. This Archimedean Solid consists of the faces from both the Cube and Octahedron. We will discuss this form in more detail in the section on F-Orbitals.
By considering these orbitals as a collective occupying a cube of space, we can relate it to the geometric forms that underpin their appearance. The P and D-orbital configuration of the atom is exactly modelled by an Octahedron and Cuboctahedron nested inside a Cube of space.
Key point
The P and D-orbital configuration of the atom is exactly modelled by The Corners of an Octahedron Nested in a Cuboctahedron.
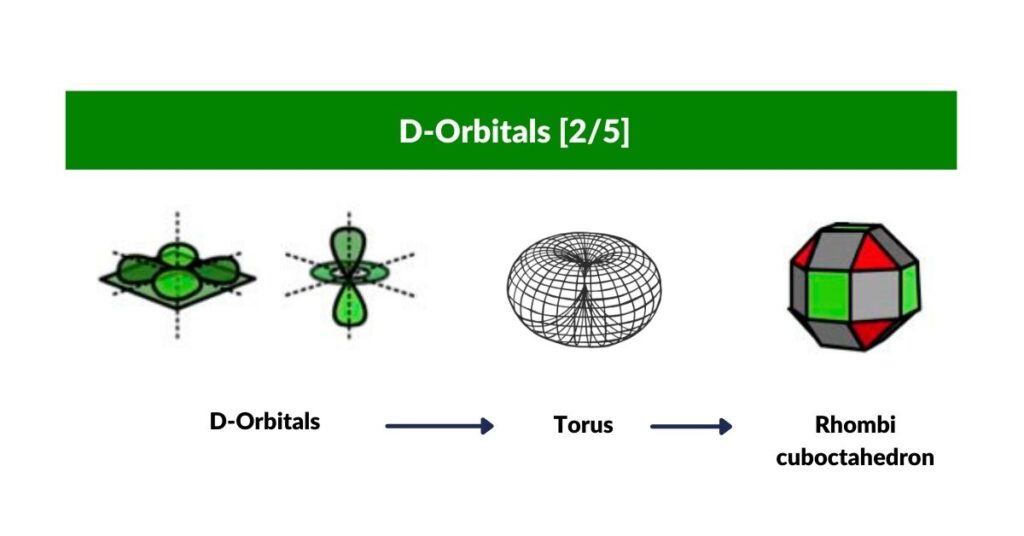
D-Orbital Torus and the Rhombi-Cuboctahedron
With three of the cross shaped D-orbitals dealt with, let us look at the orientation of the 4th. This orbital is rotated at 45° to the existing D-orbital along the x, and y-axis. When the two are viewed together, it produces an Octagon.
The final orbital is of a completely different nature to the rest, as we suggest it expresses the nature of a torus field, with a lope extruded in a north and south orientation. The 45° octagonal D-orbital appears on the same plane as the torus ring. In consideration of theses geometric qualities, we postulate that it is the Rhombic-Cuboctahedron, which serves as a container. The midsection is an octagonal prism that can rotate freely, whilst the two ‘caps’ are held in place. Out the whole set of 13 Archimedean Solids, the Rhombic-Cuboctahedron is the only one that exhibits this quality. On top of that, it is the perfect form to map the final two D-orbital electron pairs.
Explore that geometric nature of the D-orbital elements in more detail
D-Orbital Geometry – Part 2
The 2nd set of D-orbitals contain various anomalies that are explained by the Geometric model…
D-orbital Geometry – Part 1
D-orbitals form cross shapes lobes that unify on the x, y, and z axis to…
D-Orbital Geometry – Part 3
The 3rd set of D-orbitals are the last to form stable elements. The geometric explanation…
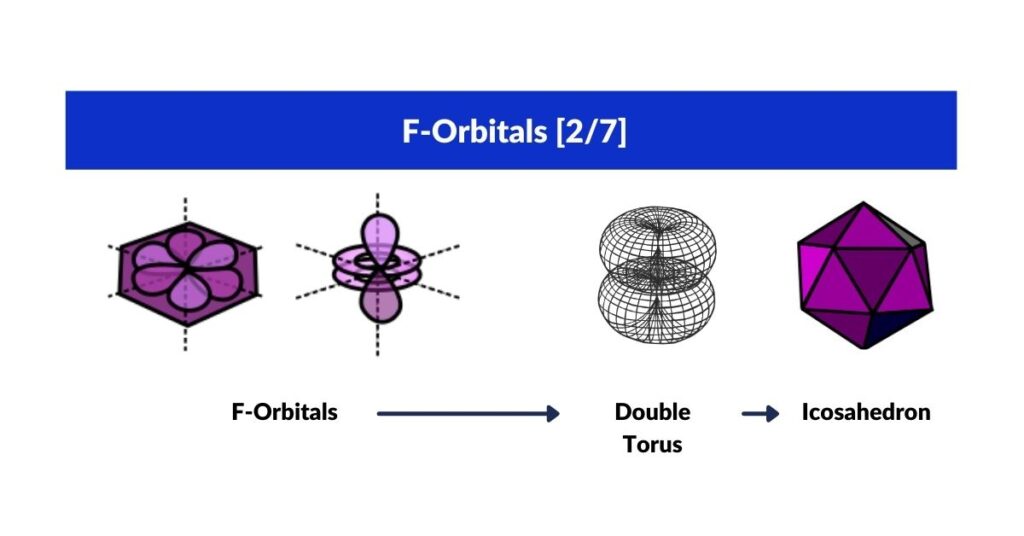
F-Orbitals
The final orbital type are F-orbitals. These appear extrapolated from the order of elements in rows at the bottom of the periodic table. Just as with the D-orbitals, the periodic table suggests that the F-Orbital appear in the 5th and 6th shell of the atom. However, there is only one stable set of F-orbitals, which appears spatially in the 4th shell. The second set (elements 89-103) are radioactive.
NOTE: It is quite strange that within this radioactive block, two elements, Thorium (90) and Uranium (92) still exist on planet earth. Technically, these elements should have decayed into non-existence, if they were created at the point of the Big Bang, just like all the other radioactive elements of this group. By accelerating the decay of (or depleting) Uranium or Thorium, all other ‘naturally’ occurring radioactive elements (91 and 89-84) are generated. The heat that is being emitted in this reaction is commonly used in the generation of energy in nuclear power plants.
Any elements above 92 include Plutonium (93), however, this is only found as a trace element embedded in Uranium ores. Beyond this, we have all ‘artificial’ elements up to 100 that have only been synthesised in the lab and never in macroscopic quantities. Atoms beyond that point exists for only fractions of a second, collapsing within the blink of an eye.

F-Orbitals and the Cuboctahedron
Whereas D-orbitals from a ‘cross’, the most common orbital configuration found in the F-orbitals are hexagonal. There are four sets in total that have been defined to fall along an x, y and z axis. At this juncture, our Atomic Geometry model takes a different view of these orientations. These four hexagonal rings are the perfect fit for a Cuboctahedron. We have shown that an Octahedron combines triangular faces with the internal geometry of three squares. The Cuboctahedron has both, square and triangle faces, with an internal geometry made of four hexagons.
Viewed like this, the complete set of orbitals follow a simple expansion, from the triangle and square, to fulfil the blueprint with the hexagon. In 3D, this transformation follows the sequence of an Octahedron, transforming through the Cube into a Cuboctahedron.
F-Orbitals and the Rhombic-Cuboctahedron
F-Orbitals and the Star-Tetrahedron
Amidst the F-orbitals we find a rather unique looking cubic shaped pair. These are the only orbital types to exhibit a three dimension space. Closer examination reveals that each electron is contained with a tetrahedron. When the two interlock at 180° opposition, they define the corners of a Cube.
In geometry, this shape is called the Star-tetrahedron. What is interesting about this form is that it contains an Octahedron at its centre. By adding 8 tetrahedra to each face of an Octahedron, the Star-Tetrahedron is created. Just as the P-orbitals begin the atomic structure with an Octahedron, the F-orbitals terminate at the Star-Tetrahedron.
Key point
The P-orbitals begin the atomic structure with an Octahedron, the F-orbitals terminate at the Star-Tetrahedron.
D-Orbital Torus and the Rhombi-Cuboctahedron
F-orbital torus and the Icosahedron
There is one last orbital left that we have yet to discuss. Whilst D-orbitals exhibit a torus orbital, within the F-orbital configurations we find a double torus. This can be viewed as a 5D hypersphere, which we have assigned the Icosahedron to.
Just as the Rhombic-Cuboctahedron is only one Archimedean Solid that exhibits a ‘rotational’ property, the same can be said of the Icosahedron from the set of 5 Platonic Solids. Deconstructed into three sections reveals a pentagonal middle prism.
The pentagon contains the Golden Ratio (1:1.618), a particular proportion found throughout nature which relates to √5. Whilst many people have heard about the Golden Ratio, the Silver Ratio, is not so well recognised. The Silver Ratio is related to the Octagon, based on √2.
Similar Models
As a quick comparison between atomic models, we would like to present a table, which explains the various advantages and disadvantages of atomic geometry, compared to the Copenhagen interpretation, the Pilot Wave model and the MCAS model. The MCAS model is probably the least well known.
Find out more about the history of the atom
Geometric Theory of the Universe
Atomic Geometry presents a complimentary model of the Atom that is compatible with existing models such as the Copenhagen interpretation and the De Broglie Pilot Wave Model. However, it also brings new concepts to the arena of quantum physics.
From the perspective of Atomic Geometry, we suggest that the nucleus of every Atom is surrounded by a particular type of geometric space. This gives rise to the quantised energy states, a fundamental characteristic of all quantum investigation. Yet, as to how this may occur has never been fully explained.
We propose that this space is not just three dimensional. In fact, orbitals have been noticed to exist in the fourth dimension and we postulate possibly the fifth. By this, we do not mean abstract concepts of dimension based on string theory rather than 1D, 2D, 3D, 4D and 5D axioms based on Euclidean geometry, such as the Platonic and Archimedean Solids.
THE
Conclusion
What does this tell us about the Atom?
Unlike other models of the atom, Atomic Geometry provides a clear description, that can be modelled using simple geometry. This makes understanding the sub-orbit structure far more simple than any other model of the atom.
Atomic Geometry: a fresh perspective.
Atomic geometry is applicable to the electron cloud that surrounds the hydrogen atom, from which the scientific data of the S, P, D, and F orbitals have been collated. It offers a clear view of the fractal nature of space. The same structures can also be seen to organise other physical phenomena too, such as the planets of our solar system. This in turn lends us to a new geometric model of the universe that begins to solve some of the most perplexing problems facing traditional atomic models.

Read More about Atomic Geometry
Browse more interesting post from the list below


Brillouin Zones and the geometry of Ferromagnetic and Electrically Conductive Waves
The idea that electrons moving though a wire produces electrical flow was disproven over 100 years ago. The Brillouin Zones are used to map the electron waves, which exhibits a particular geometric structure.

D-Orbital Geometry – Part 2
The 2nd set of D-orbitals contain various anomalies that are explained by the Geometric model of the atom. Part 2 of 3.
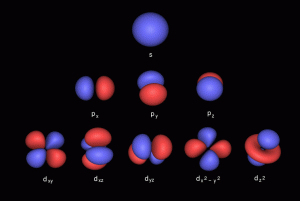
2D Orbital Geometry of the Electron Cloud
The 4 types of electron orbital can be mapped to 2D geometry, called the Seed/Flower of Life. This produces a simple geometric pattern that decodes the electron configuration.
YOUR QUESTIONS ANSWERED
Got a Question? Then leave a comment below.

Question?
This post seem quite straight forwards, but why hasn’t science recognised this geometric nature?
ANSWER?
We have tried to approach the scientific community with our ideas. Unfortunately, we have not had much success. This might be because QM is generally involved with quite complicated mathematics, and so the geometric model, and its simplicity, may not be taken seriously, simple because it is so easy to grasp

Question?
Is this model of the atom applicable to all the elements on the periodic table?
ANSWER?
Data about the S, P, D, F orbital shells has been gathered by ‘pumping’ energy into a hydrogen atom. Science uses hydrogen as it is the simplest atom to work with. However, as it does not exhibit a neutron, like all other atoms, the atomic radii changes as we move through the periodic table. We have a more advanced model of the atom called geo-quantum mechanics that produces the most world’s accurate description of all stable elements in terms of atomic radii.