D-orbitals are the third type of electrons to appear in the atom. In this article, we will explore the geometric nature of the first set of these elements (20 to 30) and the reason for the electromagnetic properties of Iron and Copper, that appear within the set.
Overview
KEy Points
-
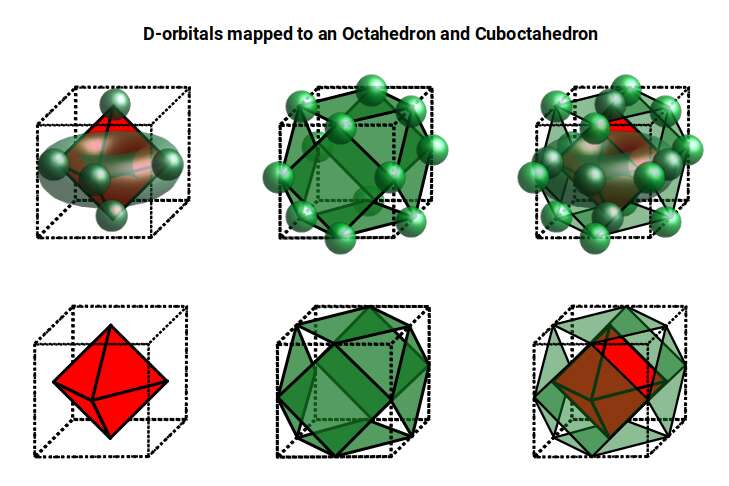
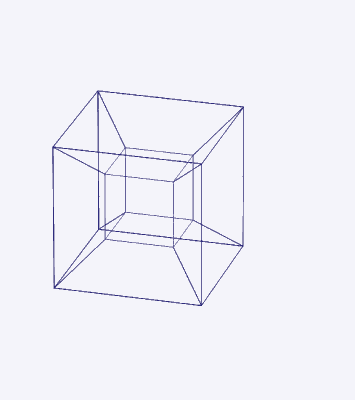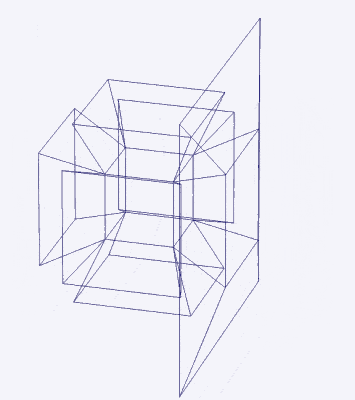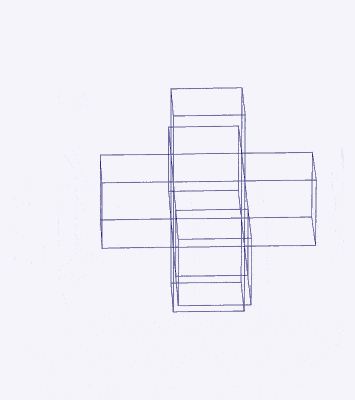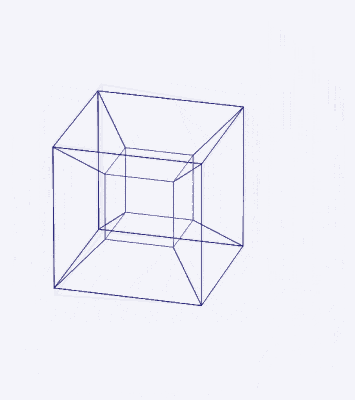
D-orbitals form a Cuboctahedron that is nested within a Rhombic Cuboctahedron, produced from the exstended jitterbug modle
-
The geometric structure of the D-orbital conforms to 4D geometry, found in the Rhombic Dodecahedron whose shadow projection creates the nested set.
-
The ferromagnetic and conductive qualities of the D-orbital elements can be ascribed to the shapes of each geometry as it trasforms through multidimensional space.
This article is a continuation of a series that explains in detail our new theory of atomic geometry. You can find out more about the S-orbital and P-orbital types in other article on our site, which cover some of the key geometric principles explored below.
S-orbital Geometry
S-orbitals form the only set of elements occupying a spherical shell. Whilst quantum theory suggests it is 'only applicable' to these types of atom, investigation of the atomic radius shows a discrepancy of over 100% for some elements.
P-orbital Geometry
P-orbitals form in sets of 6 producing an octahedral structure. By producing this form based on the average radii for each set, we can approximate the radius for almost all elements on the periodic table.
What is an orbital?
An atom comprises a nucleus of protons and neutron, surrounded by a field termed the electron cloud. The number of protons and electrons increases in a 1 to 1 ratio to produce all the different types of atoms on the periodic table. This gives each element its atomic number starting at hydrogen (1), and ending at Bismuth (83), after which the non-stable radioactive elements appear.
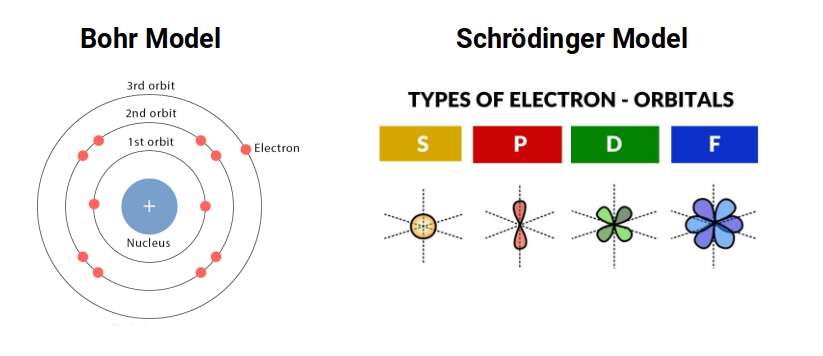
Whilst it is common to represent these shells as concentric circles, each containing a certain number of electrons, in truth there are 4 different types of sub-orbital arrangements. These are labelled S, P, D, and F, each of which forms a particular geometry. This model is based on the Schrödinger equations developed in the 1920s to account for the problems with the concentric ring interpretation of the Bohr model.
Whilst the Bohr model is still often used to describe the atom, it has been scientifically proven to be incorrect. If the electrons were particles travelling around the nucleus, they would need to be moving faster than the speed of light. Furthermore, the electron’s radius has never been established. Presently, in more advanced fields of physics, it is more common to treat the electron as a point of charge. Therefore, each orbital lobe represents an area where the electron is likely to be found.
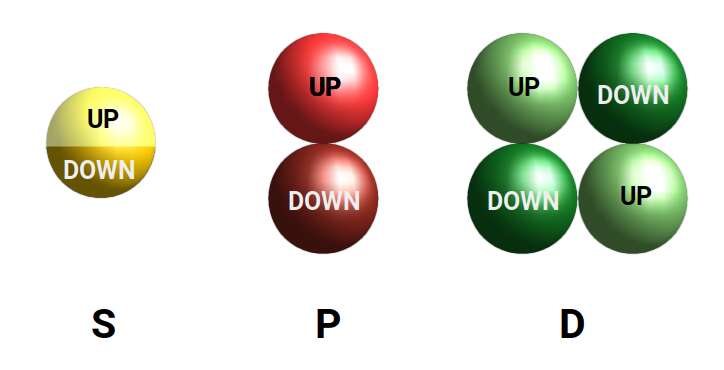
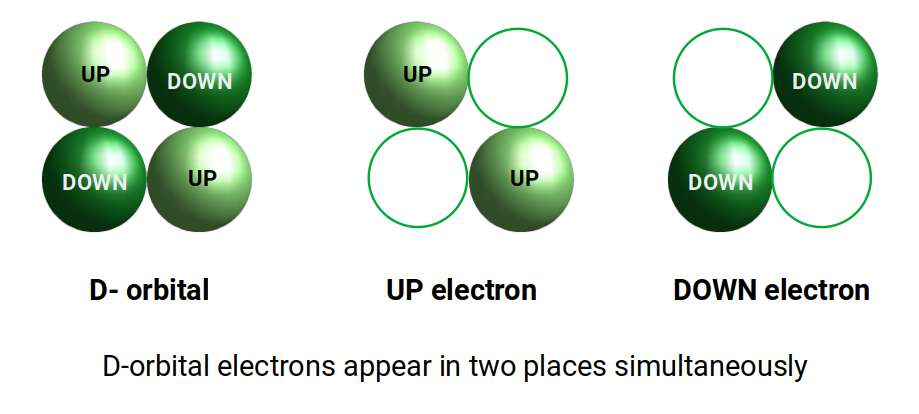
Whilst electrons do not circle the nucleus, they do exhibit a quantum spin value, that can be in only 1 of 2 states, UP or DOWN. This notion of spin has nothing to do with a rotating particle, and is more accurately described as intrinsic angular momentum. The electron maintains a conservation of angular momentum as if it were rotating, which when aligned with other atoms produces a magnetic field.
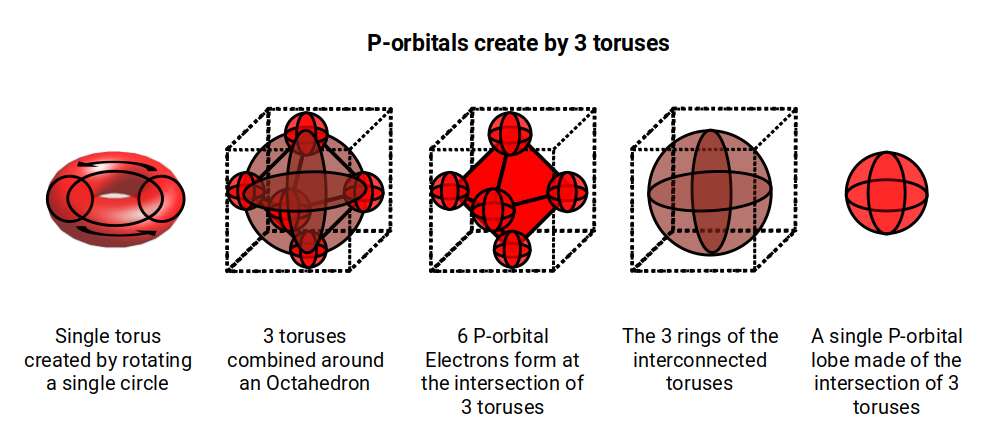
When we consider the first 3 orbital types, we can notice that a particular geometric pattern emerges. The S-orbital appears as a single sphere made up of 2 electrons, the P-orbital appear as 2 spheres that appear either side of the nucleus, and the D orbitals appear as 4. What becomes apparent is that as each step, the number of lobes doubles.
This curious behaviour exhibits a specific geometric structure, that expands through dimension, from the dot (0D) or sphere, to the line (1D) to the square (2D). In our article on 2D orbital geometry, we explain in great detail the reason for this, which introduces a 4D geometric interpretation of the electron cloud.
orbital Configuation
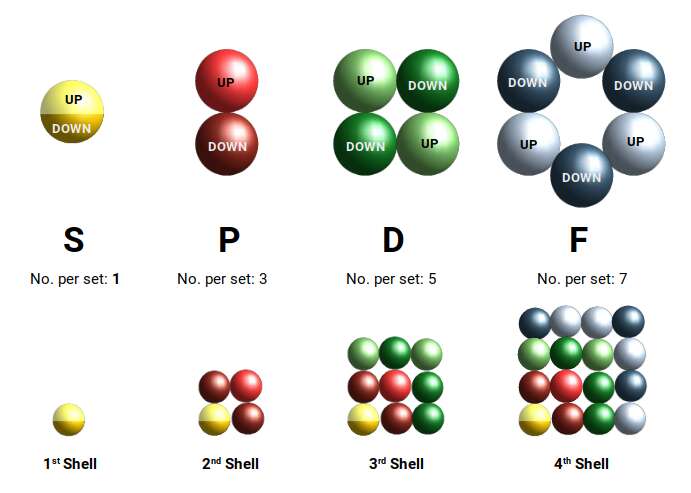
The electron cloud is structured in such as way that, for each successive shell, the next set of orbitals is added to the set. The 1st shell can only hold 2 electrons, which form a single S-orbital. Then the second shell begins by completing an S-orbital, followed by 3 sets of P-orbitals. The D-orbitals first appear in the 3rd shell, after a set of S-orbitals form in the 4th.
D-orbitals always come in sets of 5. Notice that this forms a series of numbers, from 1 S-orbital, to 3 P-orbitals, to 5 D-orbitals. The final F-orbital type comes in sets of 7. In each case, the number of sets expands through an odd number series. As each subsequent shell adds another orbital type, we can total up the number of orbitals in each to produce a square number series.
You might think that this pattern would continue beyond the formation of the F-orbitals in the 4th shell. However, the 5th shell only forms S, P and D orbitals, and by the 6th shell only the S-orbitals form as a complete set, along with just 3 P-orbital elements. After this the radioactive elements begin. This means there are three sets of D-orbitals, that appear in the 3rd, 4th, and 5th shells of the electron cloud. This accounts for 30 elements on the periodic table, more than any other orbital type.
D-orbital Elements
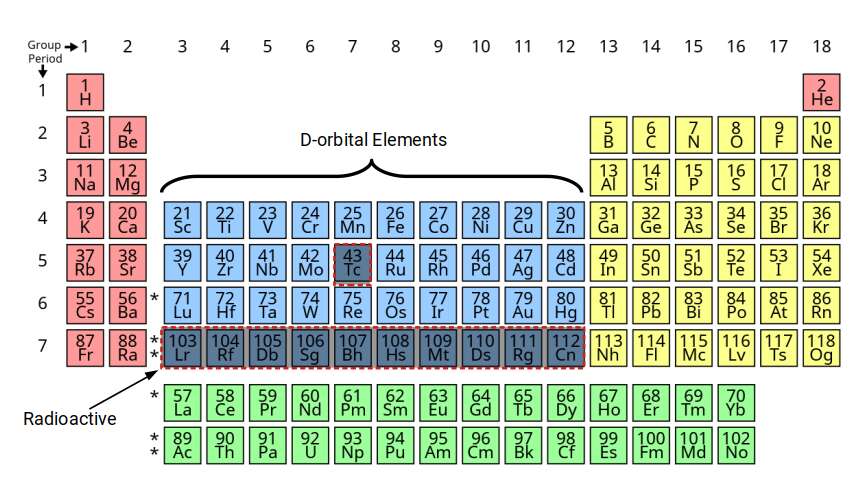
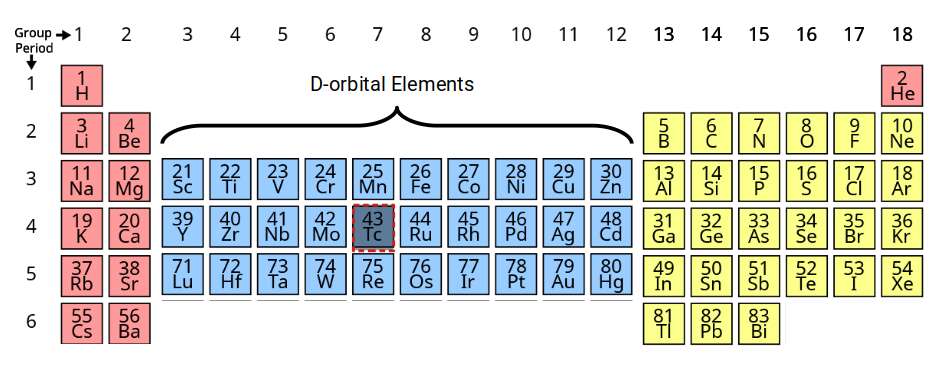
D-orbitals appear on the periodic table between the S and P-orbitals, groups 3 to 12. These elements are also called transition metals due to their position. Normally the periodic table lists 4 blocks of D-orbital elements, however, the 4th set is formed of radioactive elements, that decay into elements with a lower atomic number. Additionally, element 43 in the middle of the set is also mysteriously radioactive. This occurs at the halfway point of the 3 sets of stable D-orbitals. Present theory offers no tenable explanation for this strange occurrence. We will examine the reason for this in the 2nd part of this D-orbital series.
Notice that the standard periodic table places the D-orbital sets in the 4th row. This is unfortunate, as it often leads students to believe that the stable D-orbitals appear in shells 4 to 6, rather than 3 to 5, as is actually the case. Quite why chemistry has adopted this misconfiguration of the orbital shells has no justifiable reason, other than to maintain the sequential numbering of elements across each row.
Yet, this confuses the nature of D-orbital elements, which normally only appear with a completed S-orbital set in the shell above. A more accurate description of the structure of the electron cloud can be presented by moving the D-orbital set into the correct shell number. Once we remove the radioactive elements from the table, an interesting symmetry begins to emerge.
Viewed in this light, the D-orbitals do not transition between the P-orbital types, and are instead formed inside a shell that already has a complete set of S-and P-orbital elements. The miscellaneous radioactive element, Technetium (43), appears in the middle of the set. We can count off exactly 34 elements before it, down to hydrogen (1), and after, up to the last, Bismuth (83). This fact is not recognised by the traditional model, for several reasons. Firstly, this table of elements excludes the F-orbital types and the radioactive elements. Secondly, the D-orbitals are normally represented in the 4th, 5th, and 6th, rows, whereas this table is based on the electron configuration of the atom.
What we will show is that the organisation of elements has a profound geometric reason, which begins to answer why there are certain anomalies found within the structure of the electron cloud. As geometry can also be translated into ratio, our theory of Harmonic Chemistry, explores the structure of the periodic table from the perspective of music theory.
D-orbital Sets
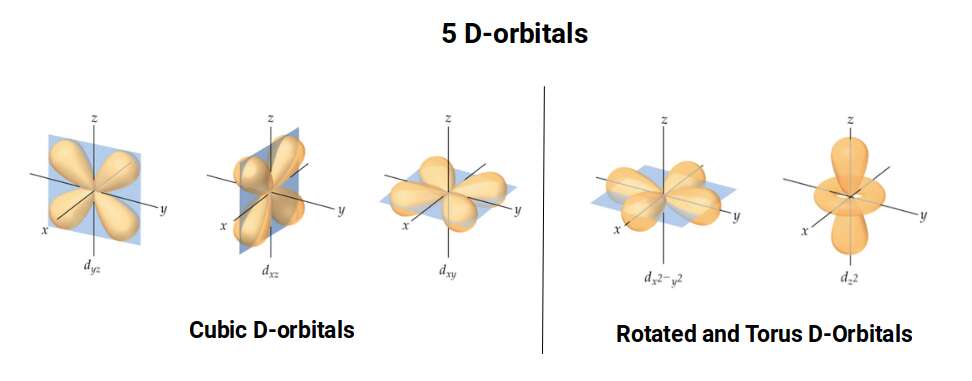
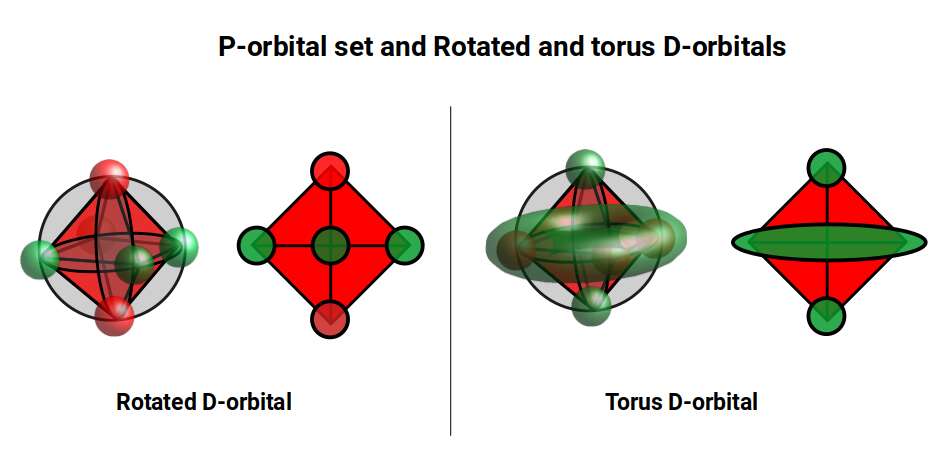
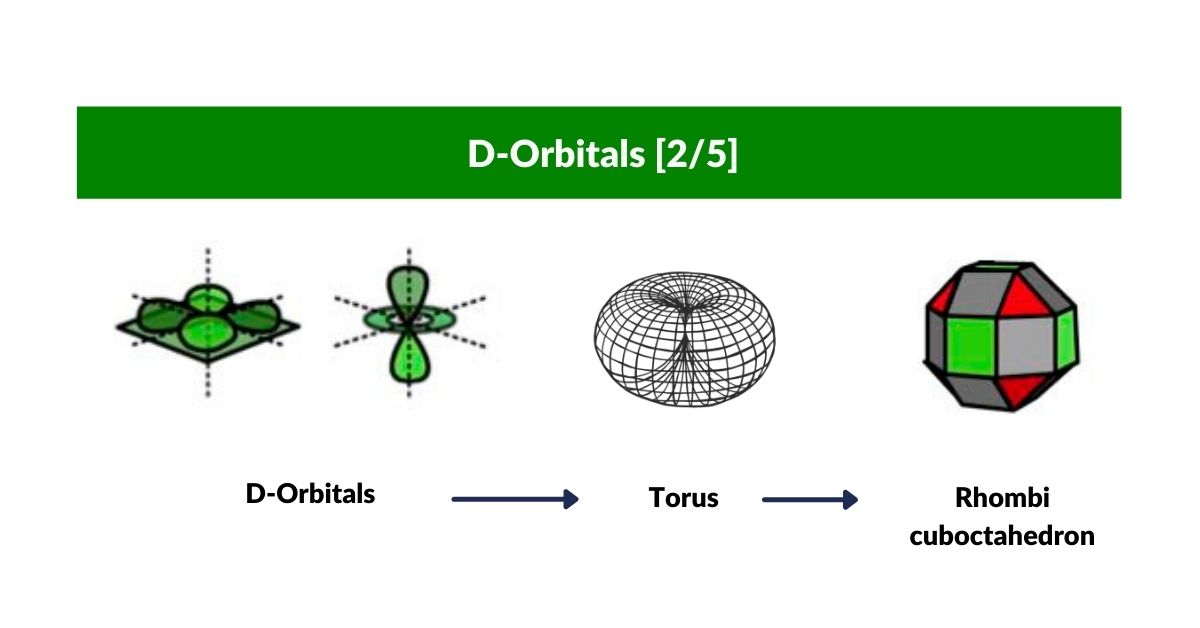
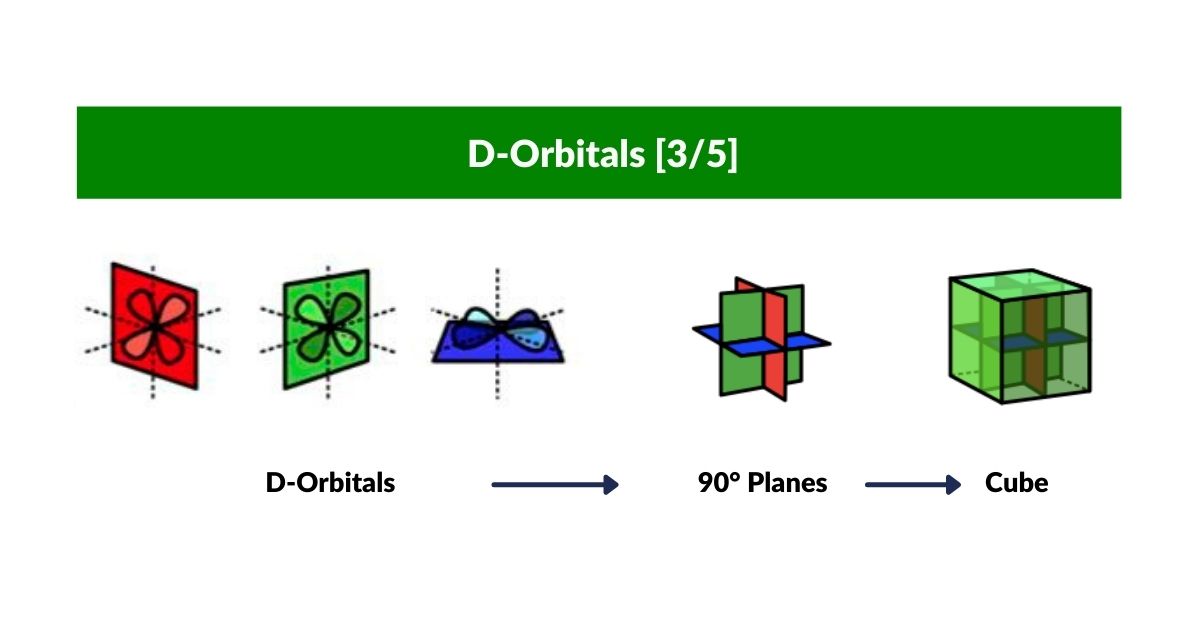
D-orbitals come in a set of 5 different types, of which 4 are shaped like a cross, with a 5th that appears as a torus shape with a pair of orbital lobes defining the north and south poles. Out of the cross shaped type, 3 can be combined to form square planes that divided a cube of space through an x, y, and z axis. The 4th cross shaped orbital is rotated at 45° on the x, y plane. This falls over the torus orbital ring of the 5th orbital. We can separate these orbitals into two sets, 3 that form the cube, and the other 2 that create the Torus.
The D-orbitals form after the P-orbitals, which always come in sets of 3. Each is positioned on the x, y, and z axis, in the same orientation as the Cubic set of D-orbitals. In the theory of Atomic Geometry, the combined set forms the geometry of an Octahedron. This is a Platonic solid that exhibits 6 corner points. From the perspective of a 4D electron cloud, the P-orbitals are each assigned the geometry of a torus field, which wraps around the edges of the Octahedron. The 3 cubic D-orbital electrons all fall in the midpoint of the side of the Octahedron. Dividing it into 8 parts.
The 4th cross shaped D-orbital is rotated at 45° on the horizontal plane. This means that it appears superimposed over the 2 sets of P-orbitals on the x and y-axis. The torus orbital also produces a ring over the same set, with the top and bottom lobe occupying the vertical position, where the 3rd P-orbital is found. Therefore, these 2 D-orbitals sets appear in exactly the same orientation as the P-orbitals.
The reason that these D-orbitals appear superimposed over the P-orbital set is not explained by the present theoretical models of the atom. Yet, the result is an ordered geometric configuration that can be mapped to two nested 3D polyhedra. The cubic D-orbitals fall into the space in between the P-orbitals, which defines a Cuboctahedron. The rotated and torus orbitals fall in the same place as the P-orbitals, and are represented by an Octahedron.
In our examination of the P-orbital Geometry, we explained how the Octahedron transforms into a Cuboctahedron through the Jitterbug Transformation that we will discuss in much more detail shortly. The D-orbital set appear to map both of these combined polyhedra in a single orbital set.
4th dimensional D-orbital Geometry
The appearance of the torus shaped D-orbital is suggestive of the 4D nature of the electron cloud. The torus is a 4D shape that is generated by a circle, (or sphere), that is rotated around a central axis to complete the form. In our examination of the P-orbital sets, we attribute the mysterious movement of the electron, from one orbital lobe to the other, to the unification of 2 toruses orientated at 90° to each other. By the time the set completes, Three toruses form around the sides of the octahedron. Each P-orbital lobe now becomes defined by the 3 intersecting circles, forming the internal geometry of a sphere.
The D-orbitals all form within the Toruses of the P-orbital set. The 3 cross shaped cubic orbitals appear in between the S-orbital lobes, whilst the other 2 appear superimposed over the P-orbital set. The cross shaped D-orbitals are each comprised of 2 electrons, with either an UP or DOWN quantum spin value. This seems rather odd from the electron particle perspective. When trying to locate the particle, the act of measuring can only determine a single place where the electron exists. If we separate out the two lobes, we can see that each electron falls into two places. This indicates that the electron is not a particle as is commonly presumed, but is present in two places at the same time.
This concept has nothing to do with quantum superposition, which is derived from the nature of electron spin, and the difficulty in defining the electron as a particle. The standard model suggest the orbitals are probabilistic in nature, but does not consider the electron as purely a wave phenomena. This is due to the fact that current theory disregards the background energy of space, sometimes referred to as the Aether.
Yet, the vacuum energy is a scientific fact, which is the reason why the speed of light is constant. Once we reintroduce the notion of this energy field, into which all atoms are immersed, then the orbitals begin to take on a more defined nature. Each lobe represents an area of space where an ‘electron’ can appear. We suggest this is due to the increased energy density of that region of space, which is generated by the quantum ½ integer spin values of the field. For every 360° rotation in 3D space, the electron must rotate 720°. These are sometimes described as Spinors, however, from the perspective of geometry, this nature can be accounted for by the rotation of a 4D polytope. We explain this new perception in greater detail in our article on the 4D electron cloud.
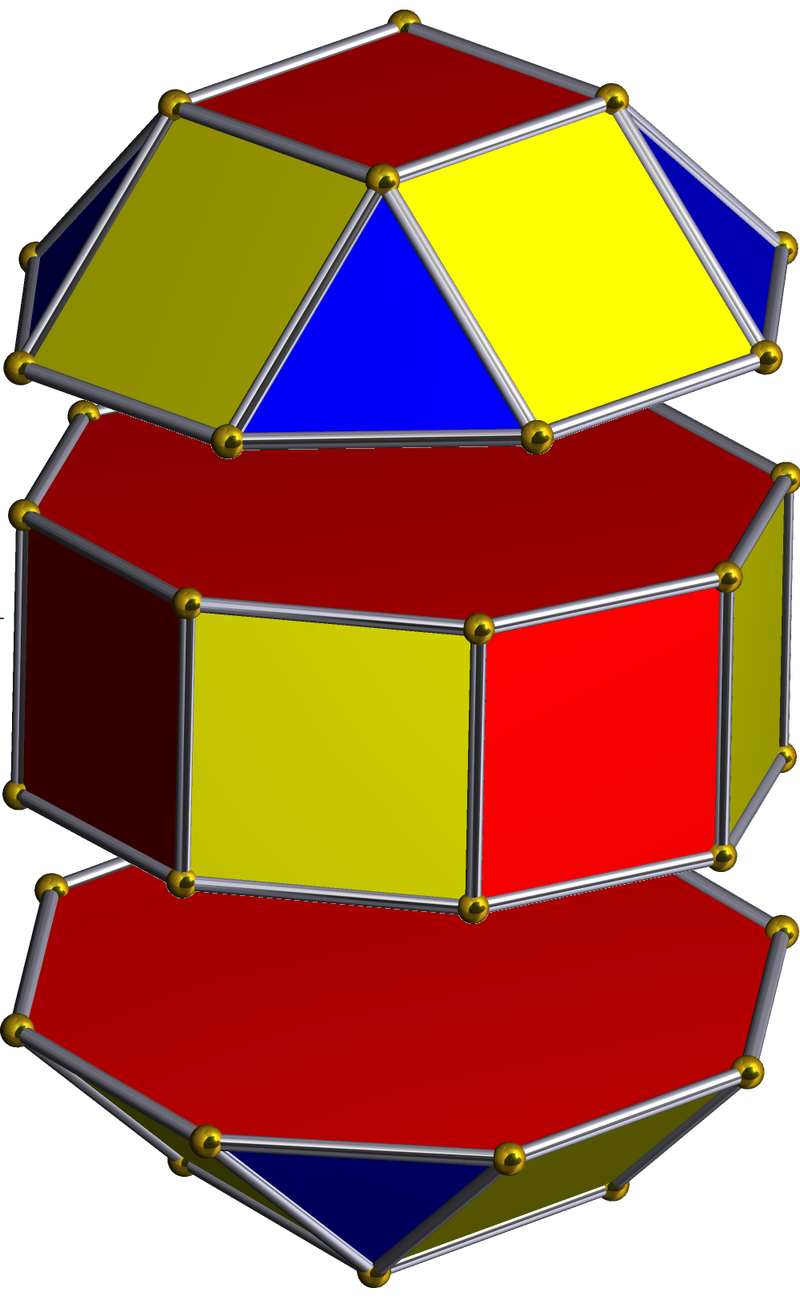
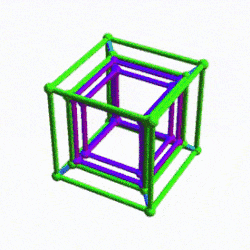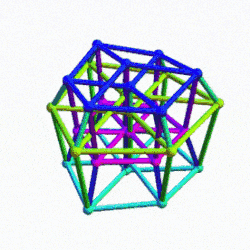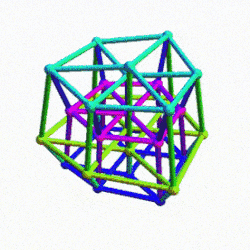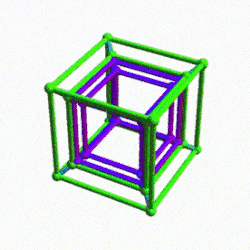
The Rhombic Cuboctahedron and the torus D-orbital
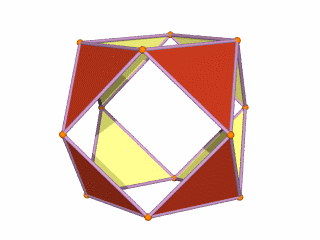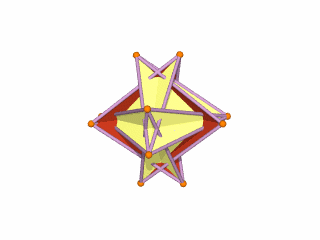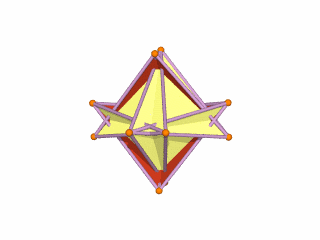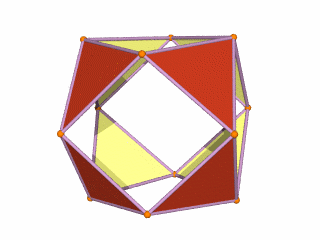
Whilst the cross shaped D-orbitals can be easily matched to the corners of a Cuboctahedron, the remaining torus orbitals seem to be slightly out of place. In Atomic Geometry, we represent these D-orbitals with the Rhombic Cuboctahedron. This is an Archimedean Solid that is composed of the sides of a Cube and Octahedron, which move away from the centre, to leave an additional 12 empty square spaces. These can be filled to produce the Rhombic Cuboctahedron. A similar process generates the Rhombic Cuboctahedron from the Octahedron.
The Rhombic Cuboctahedron formed from either a Cube or Octahedorn
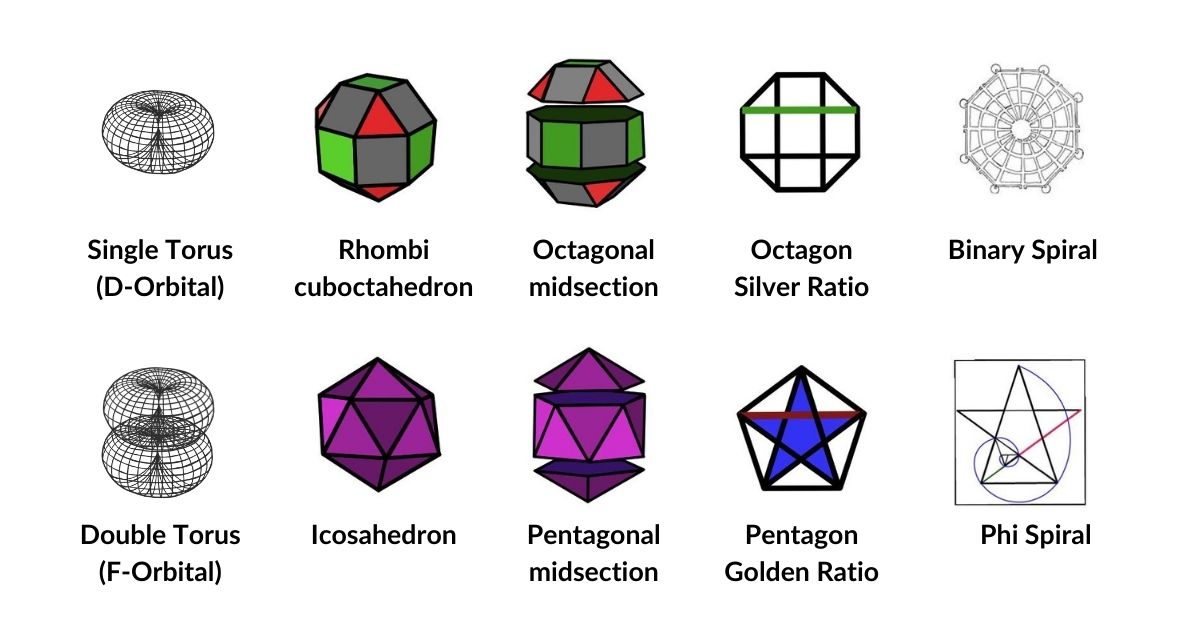
The unique quality of the Rhombic Cuboctahedron is that it is the only Archimedean Solid that exhibit an octagonal midsection. This prism is free to rotate between the 2 caps, in 45° increments, just like the orientation of the D-orbitals on the central plane. This makes it the ideal solid to represent the torus orbitals.
Aside from the Rhombic Cuboctahedron, the only Platonic Solid to exhibit a similar nature is the Icosahedron. Whilst the former exhibits square faces and forms an octagon, the latter expresses triangular faces and forms a pentagon at its centre. Geometrically, the octagon creates the Silver ratio, based on √2±1, whereas the pentagonal midsection of the Icosahedron expresses the Golden ratio, (√5÷2)±½. We will discuss these 2 important geometric concepts as we examine the D-orbital configuration in more detail. In Atomic Geometry, the Rhombic Dodecahedron is assigned to the D-orbital torus, whereas the F-orbitals exhibit a double torus mapped to the Icosahedron.
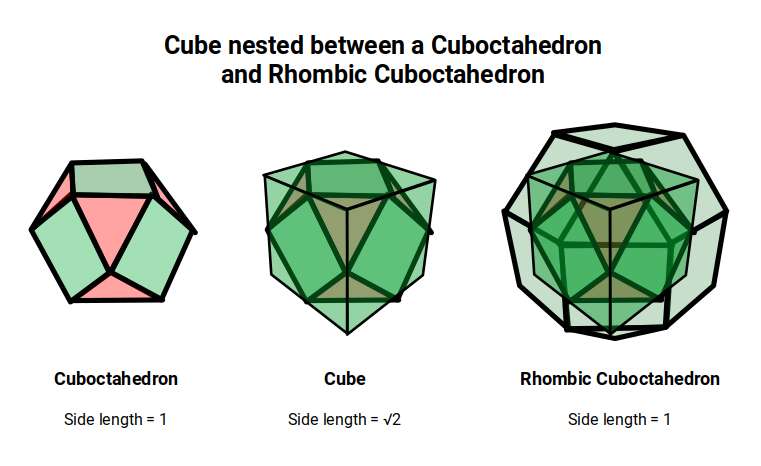
A Cube can be nested inside a Rhombic Cuboctahedron so that its corners touch at the centre of each triangular face. If the Rhombic Cuboctahedron has a side length of 1, the Cube will have a side of √2. Additionally, a Cuboctahedron can be formed by truncating the corners of the Cube, that will have a side length of 1. In this way, we find that the complete set of orbitals can be perfectly orientated within this nested set of polyhedra.
4D geometry and the Silver Ratio
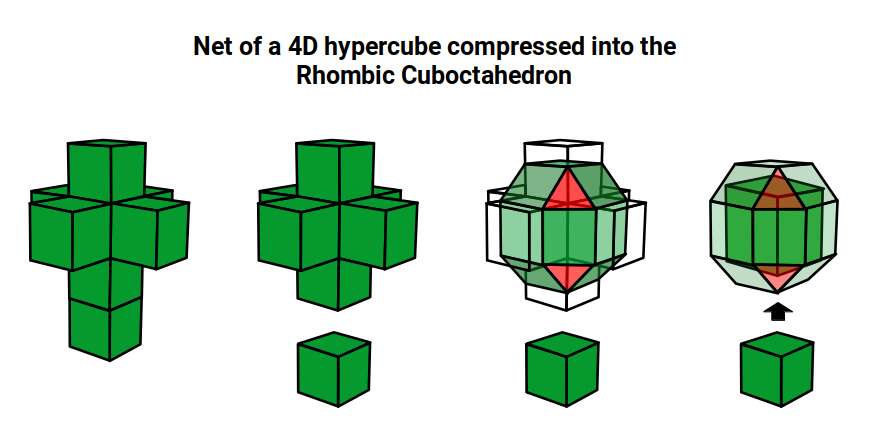
The 4D hypercube can be envisioned as two cubes that appear superimposed over the same space in 3D. These can be separated into two parts by reducing the side of one of the cubes by a specific amount. In this way, when the wireframe is projected onto a 2D surface, we can obtain an insight into the nature of the 4D polytope. In the case of the Geometric model of the D-orbitals, 2 cubes are orientated by the Rhombic Cuboctahedron. As shown previously, this polyhedron can be formed by exploding a cube so that is faces expand away from the centre. If the initial cube has a side length of 1, the second will be √2 larger.
Just as a 3D polyhedra can be created by cutting out a 2D template and folding it, the same can be said of 4D solids. The Tesseract (4d Cube) is formed by a similar net as the 3D Cube, except that the 6 square faces are replaced by 8 Cubes. A 4D polytope has 3D shaped faces, believe it or not. This template forms a 3 Dimensional cross in space that is folded in 4D space. Notice how the bottom cube that sticks out the furthest and wraps around the others, which forms the concept of 2 Cubes nested insider of each other.
We can compare this net to the model of the Rhombic Cuboctahedron. The Cube wraps around the others is already defined by the √2 Cube that nests with its corners touching the triangular faces of the Rhombic Cuboctahedron. Detaching this from the set leaves us with a central Cube with 6 more attached to each face, forming on an x, y and z axis., similar to the P-orbitals. By contracting each outer cube towards the centre, the radius becomes reduced, forming the shell of the Rhombic Cuboctahedron. In this way, we can begin to recognise how this Rhombic Cuboctahedral structure can represent the formation of a 4D hypercube.
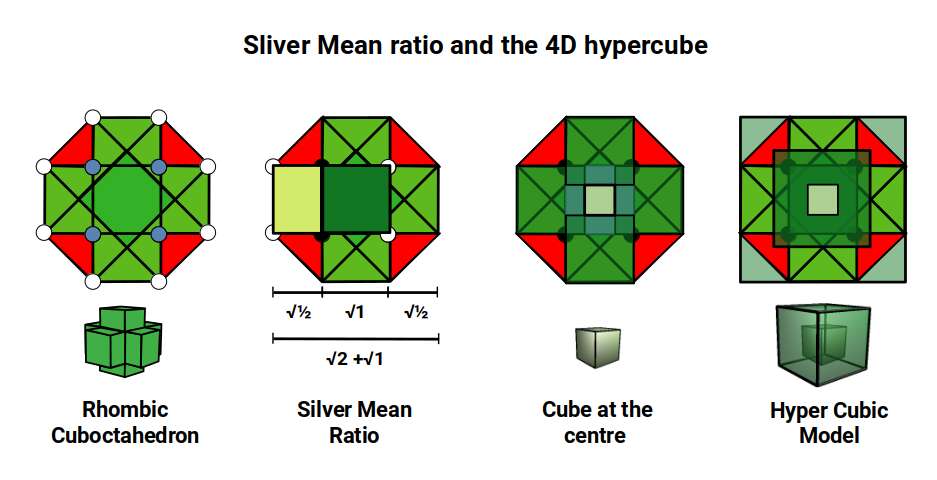
The Rhombic Cuboctahedron produces an octagon when viewed from above. This exhibits as special ratio known as the Silver Mean. Similar to the more famous Golden Mean, this ratio is based in the √2±1, which also has a root only expression (√2±√1). The unique quality of this number is that its reciprocal value switches the equation to the negative. For example, √2+1= 2.414…, which has a reciprocal value of 0.414…, or √2-1. This gives it a particular fractal quality, that can collapse into infinity through the Silver Spiral.
Let us imagine that the out cubes remain the same size as they contract to form the Rhombic Cuboctahedron. This leaves a small cubic space at the centre that is not touched by any of the external cubes. This space will have a side length of √2-1. When we consider this structure, we find it can be enclosed in a cube with a side length of √2+1. As we also have a nested cube side √2, and original cube, side 1, we find the perfect expression of the Sliver Ratio within this Rhombic Cuboctahedral structure.
This model of nested solids provides an insight into the geometric nature of the D-orbitals. The 3 cubic cross shapes orbitals form at the midpoints of the cubes sides, defining the Cuboctahedron. The remaining 2 form the torus field of the Rhombic Cuboctahedron, which orientates a larger cube (√2), by cantering its corners upon its triangular faces. The Octagonal midsection can accommodate the 4th set of cross shaped D-orbitals, orientated a 45° to the others.
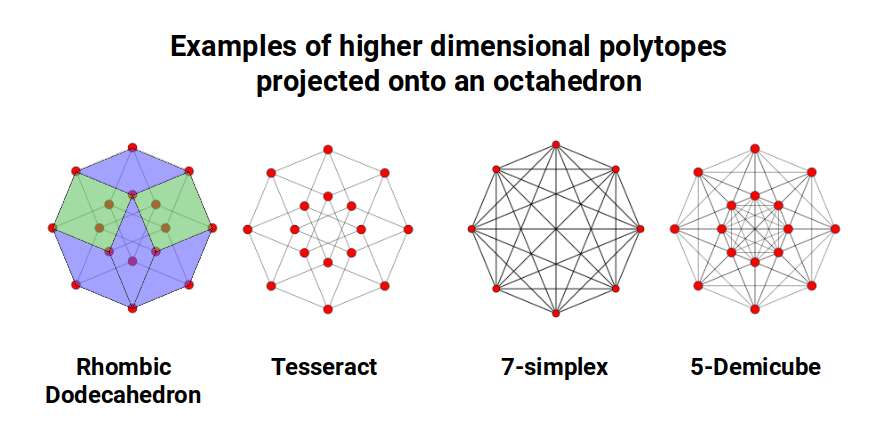
In fact, the Octagon is recognised for is capacity to produce a shadow projection of the 4D tesseract, which we will discuss in more detail shortly. However, it can also be used to define a variety of higher dimensional polytopes. This includes the 7th dimensional Simplex the 5D Demicube, which are based on the Tetrahedron.
4D Hypercube and the Rhombic Dodecahedron
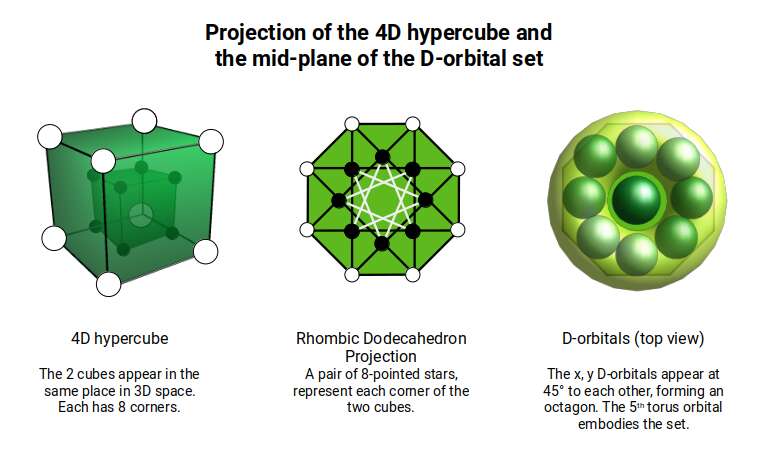
Before we continue, let us take a moment to consider the nature of higher dimensional space. A 4D hypercube can be rotated on our familiar x, y, and z axis, but it also exhibits a fourth w ‘time’ axis. This means that it can be rotated like a regular 3D cube, however, when rotated on its w axis, the cube will ‘swap’ places in 3D space as it rotates (as shown previously).
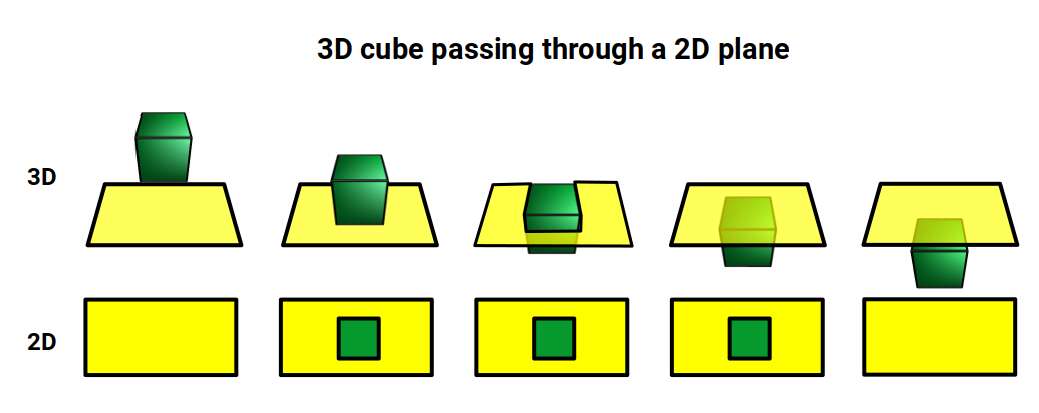
Another way to visualise a 4D object is to pass it through a 3D space. This principle also works for 3D objects projected into 2D space. For example, a Cube that is passed face on through a 2D plane will create a square the moment it touches the surface. The square will exist for a certain period of time, dependant upon the speed at which the cube passes through the plain. As soon as it exits the plain, the square will magically disappear. From the perspective of the 2D plane, a square magically appears, exists for a certain amount of time, and then disappears.
If the 2D observer knows the side length of the cube by examining the square, then by timing the duration that the square ‘exists’, will allow them to comprehend how fast the cube is moving through the plain. For example, if the cube with a side of 1 is passed through the plane over the duration of one second, it is clear the speed at which the Cube is moving is 1 unit per second. We can apply a similar concept to a 4D hypercube. Instead of passing a 3D object through a 2D plane, we can pass the 4D solid through a 3D Hyperplane.
When passed face on, as in the example above, we can see the cube seems to grow in size, forming an elongated cube, As it exits the plane it creates a square that is larger than the first by a certain amount. When passed through side-on, the hypercube traces out a Hexagonal prism, similar to a normal cube. However, again, we notice that the 4D cube increases in size as it exits the hyperplane. When passed through the w-axis, the cube will seem to grow and diminish in size, as seen in the shadow projection in the previous section.
Interestingly, each of these projections can be ascribed to the 3 types of lattice structures formed by compounds of D-orbital Elements. The Face on projection forms a cubic shell similar to the Face Centred Cubic (FCC) structure, the side on view, forms a hexagonal close packing cell (HCP), and the W-axis exhibits a cube at its centre, indicative of the Body Centre Cubic (BCC) configuration. We will discuss these in more detail at the end of the article.
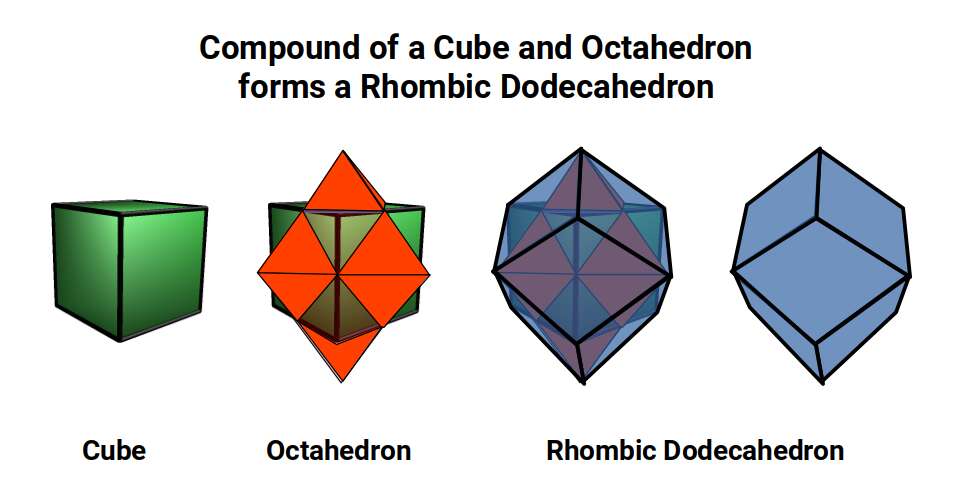
The dimensions of the dark blue frame that outlines the tesseracts passage through the 3D plane can be defined by a Rhombic Dodecahedron. This is formed from the compound of the Cube and Octahedron. The corners of each solid are joined to complete the final form.
D-Orbital and the hypercube
The Cube is the only polyhedron of the 5 regular Platonic solids that has the capacity to fill space completely by itself. Due to this nature, we use the Cube to quantify units of 3D space. Similarly, the square plane tiles a 2D space perfectly, due to the nature of the parallel lines that form its sides, but what about a 4D cube?
Whilst we are quite accustomed to the nature of 3D space and the x, y, and z, axis, the 4th dimension seems to be a much more difficult concept to grasp. Yet, its principles can be understood as the extension of lower dimensional forms. Just like a Cube, the 4D hypercube can also tile space completely by itself. This tiling is produced by the Rhombic Dodecahedron, which, like the cube, is one of the rare examples of a space filling polyhedra. 13 Rhombic Dodecahedra can be complied in 3D space in an Octahedral formation. In fact, this is actually forms a Truncated Octahedron. By adding another 6 (total 19) solids to the set, so the Octahedral shape now becomes complete.
The 4D hypercube is sometimes referred to as the tesseract, or the 8-cell. As previously stated, this can be most easily envisioned as two Cubes that occupy the same 3D space. The Rhombic Dodecahedron represents the midpoint between the transition of one Cube to the other. At the centre of the off-set cubes, a small square forms, which when projected onto a flat surface produces an 8-pointed star. This is similar to the notion of the small cube that forms at the centre of the Rhombic Cuboctahedral structure explored previously. In fact, the shadow projection of the Rhombic Dodecahedron, when projected onto a flat surface, generates the same image as our nested Rhombic Cuboctahedral image of the D-orbital set.
The conclusion is that the Rhombic Dodecahedron and Cuboctahedron are both expressions of a 4D hypercube. Whereas the Rhombic Dodecahedron forms the template of the 4D hypercube, and can fill a 3D space perfectly by itself, the Rhombic Cuboctahedral model exhibits the Silver ratio, is complied of 2 cubes, and exhibits the notion of a torus. Here we can see the mid-plane is rotated at 45°, just like the orbitals in the x, y axis of the D-orbital set.
D-orbital Radii
The radius of each element on the periodic table is defined by two main theoretical models. The Van Dar Waal Radius treats the atom as a hard spherical shell. This dataset offers a much larger radius than the experimentally determined radii for each atom. However, it does not account for the D-orbitals. The only theoretical prediction for these elements is derived from the Bohr model. However, the problem is that the predictions for the D-orbitals are out by a factor that is outside the margin for experimental error. The atomic radius is measured in Angstroms (Å), where one unit is equivalent to about 100 Picometres. The experimentally determined radii for the 3 D-orbital sets has a margin of error of ±5Å. When we make a graph which compares these datasets, we find that the difference between them is quite substantial.
|
Element
|
Radius
|
Bohr
|
|---|---|---|
|
Scandium (21)
|
1.6
|
1.84
|
|
Titanium (22)
|
1.4
|
1.76
|
|
Vanadium (23)
|
1.35
|
1.71
|
|
Chromium (24)
|
1.4
|
1.66
|
|
Manganese (25)
|
1.4
|
1.61
|
|
Iron (26)
|
1.4
|
1.56
|
|
Colbalt (27)
|
1.35
|
1.52
|
|
Nickel (27)
|
1.35
|
1.49
|
|
Copper (29)
|
1.35
|
1.45
|
|
Zinc (30)
|
1.35
|
1.45
|
|
Element
|
Radius
|
Bohr
|
|---|---|---|
|
Yittrium (39)
|
1.8
|
2.12
|
|
Zirconium (40)
|
1.55
|
2.06
|
|
Niobium (41)
|
1.45
|
1.98
|
|
Molybdenum (42)
|
1.45
|
1.9
|
|
Technetium (43)
|
1.35
|
1.83
|
|
Ruthinium (44)
|
1.3
|
1.78
|
|
Rhodium (45)
|
1.35
|
1.73
|
|
Palladium (46)
|
1.4
|
1.69
|
|
Silver (47)
|
1.6
|
1.65
|
|
Cadmium (48)
|
1.55
|
1.61
|
|
Element
|
Radius
|
Bohr
|
|---|---|---|
|
Lutetium (71)
|
1.75
|
2.17
|
|
Hafnium (72)
|
1.55
|
2.08
|
|
Tantalum (73)
|
1.45
|
2
|
|
Tungsten (74)
|
1.35
|
1.93
|
|
Rhenium (75)
|
1.35
|
1.88
|
|
Osmium (76)
|
1.3
|
1.85
|
|
Iridium (77)
|
1.35
|
1.8
|
|
Platinum (78)
|
1.35
|
1.77
|
|
Gold (79)
|
1.35
|
1.74
|
|
Mercury (80)
|
1.5
|
1.71
|
We can see the in all cases, the Bohr Model consistently predicts a larger radius for the D-orbital elements than has been experimentally verified. At best, we might be able to say that only Silver (47), an unusually large atom, falls on the boundary of the uppermost limit of the experimental margin of error. The reasons for this error are traditionally attributed to the fact that D-Orbitals form in the shell below a completed S-orbital set. Therefore, they are able to shield the outmost electron as more protons are added to the nucleus. This is called D-block Contraction.
Whilst this theory is reported as fact, investigation into the exact mathematical equations that justify the view are alarmingly absent. In truth, there is no viable model that can explain why so many of the D-orbital element should appear at roughly the same size. This becomes even more apparent when we compare the experimentally determined radii for the 3 sets in the same graph.
We can see that the 7th element for each of the 3 D-orbital sets are exactly the same size. Yet, the number of protons and neutrons that form the atomic nucleus of each element varies widely. Cobalt (27) in the 1st D-orbital set, has 27 Protons and 32 Neutrons. This dramatically increases for the elements in the shells above, yet, the radius remains strangely consistent at 1.35Å.
|
D-orbital
|
Element
|
Protons
|
Neutrons
|
Neucleons
|
|---|---|---|---|---|
|
1st
|
Cobalt
|
27
|
32
|
59
|
|
2nd
|
Rhodium
|
45
|
58
|
103
|
|
3rd
|
Iridium
|
77
|
115
|
192
|
Despite vastly different size nuclei, these elements all exhibit exactly the same radius.
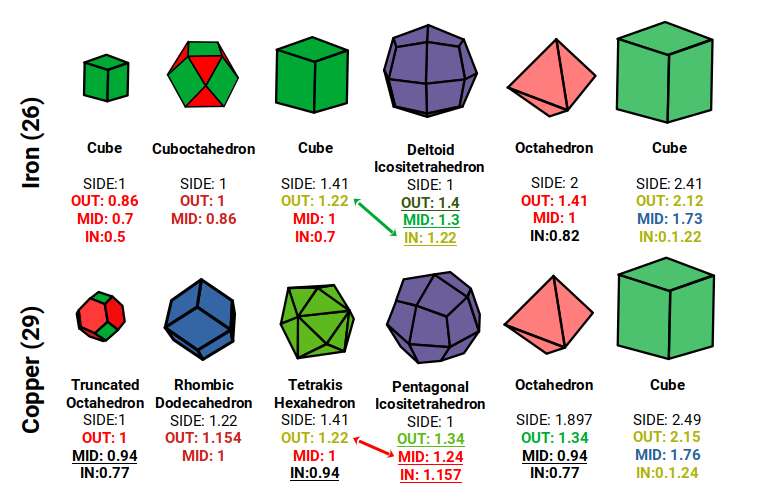
The Geometry of 1st D-orbital Elements
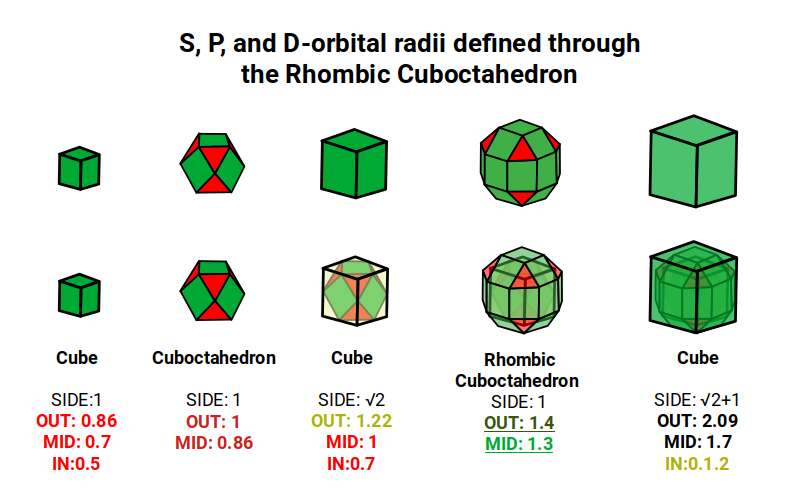
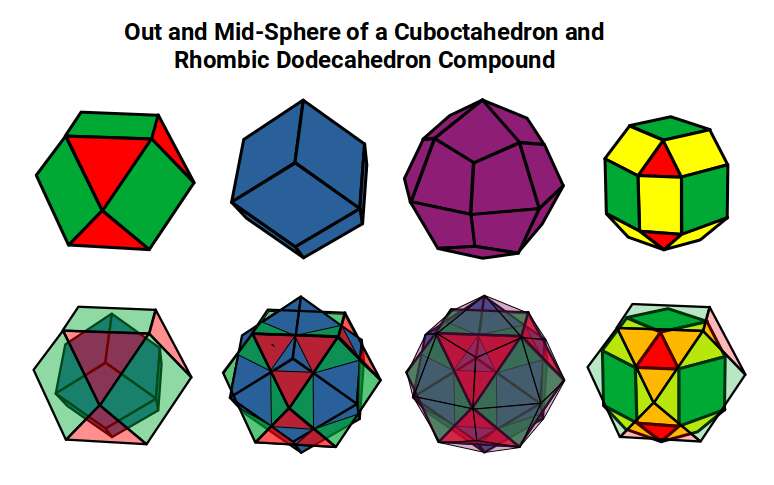
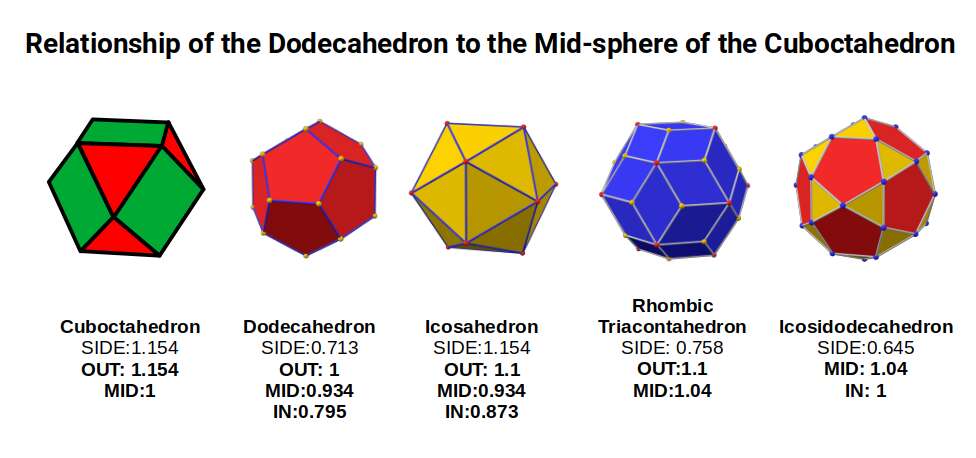
The Rhombic Cuboctahedron model of the D-orbitals nests a set of 5 different solids. There are 3 Cubes, starting with a side of 1, then √2, and finally √2+1 for the Cube that enclosed the whole structure. In the two spaces between, we find the Cuboctahedron, and Rhombic Cuboctahedron, both with a side of 1.
Each Cube exhibits an in, mid and out-sphere. The out-sphere wraps around the Cubes corners, the mid-sphere touches the middle of the Cubes sides, and the in-sphere touches the centre of each face. This creates sets of spheres with various radii. The same concept also applies to other polyhedra. Based on a Cube with a side of 1, we can map the dimensions for these spheres created by the Rhombic Cuboctahedral model.
Yellow = S-orbital Radii – Red: P-orbital Radius – Green = D-orbital Radii
A Cube with a side of 1, produces an out, mid and in–sphere which closely matches the radius of many of the 1st P-orbital Elements. Furthermore, the Cuboctahedron defines the space between the largest of the 1st P-orbital set, and the smallest of the 2nd. The Cube with a side of √2, has in and mid-spheres that also match these initial radii, along with an out-sphere of 1.22Å, the radius of Helium (2). This is the only S-orbital element that is a noble gas, and as such is completely non-reactive to other atoms.
Beyond this, the Rhombic Cuboctahedron exhibits a mid-sphere of 1.3Å, that is the smallest of the D-orbital elements, and the largest of the 3rd P-orbital atoms. Its out-sphere of 1.4 also matches 4 of the 1st D-orbital radii, marks the radii of the final elements in the 4th P-orbital set, and is also close to the radius of Lithium (3). Strangely, the Cube which encompasses the structure also exhibits an in-sphere which is close to Helium (2). We can compare these results to the experimentally determined radii, and the predictions forecast by the Bohr Model.
We can see the geometric model provides a much closer match in most cases. The Bohr Radius shows a range of inconsistencies, particularly for Helium (2), the latter half of the 2nd S-orbital set, as well as all the D-orbital elements.
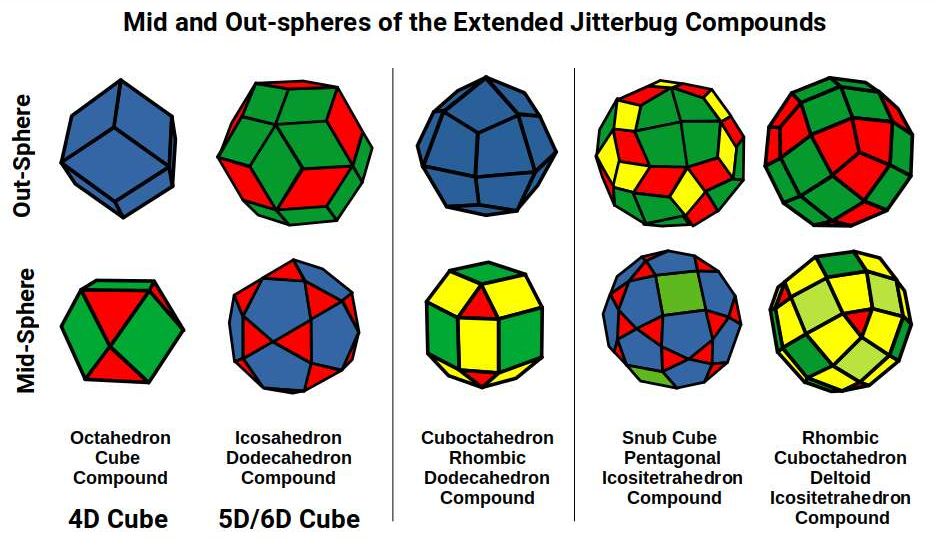
D-orbitals and the exstended jitterbug
In our previous posts that examine the nature of the P-orbitals, we explored a geometric transformation known as the Jitterbug. This process can transform an Octahedron into a Cuboctahedron by opening its sides to create a triangular and then square faces. As the distance between corners reaches 1, two triangles are formed, to produce the icosahedron. As the distance increases to √2, so the square faces of the cuboctahedron are formed. Interestingly, just like a 4D polytope, this structure can collapse, flipping itself inside out.
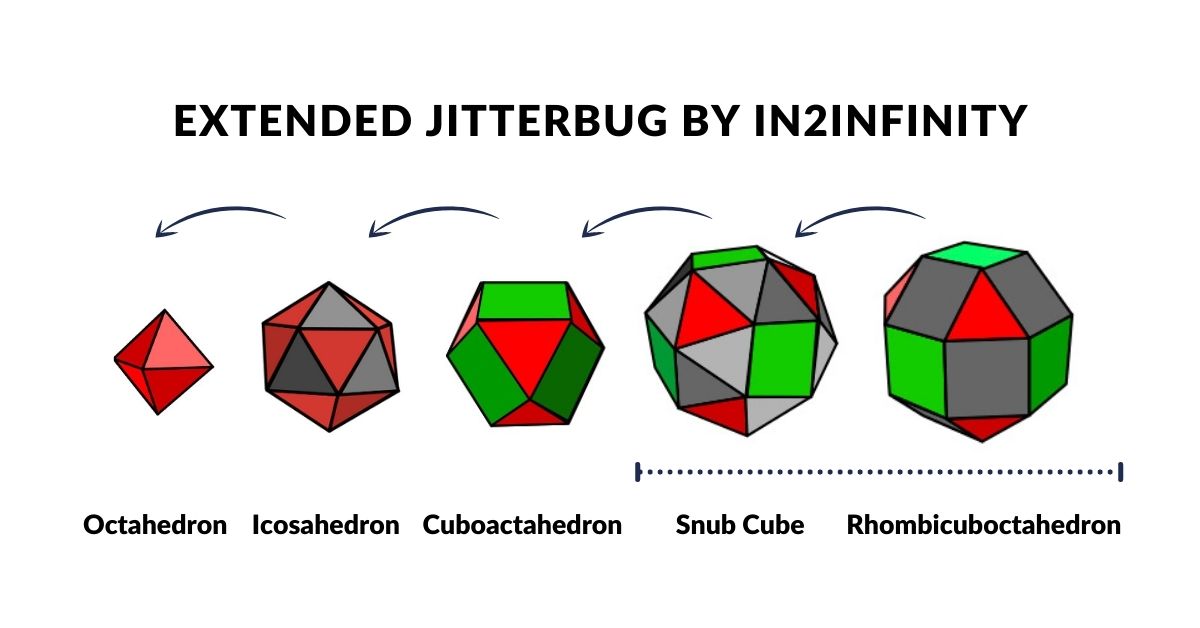
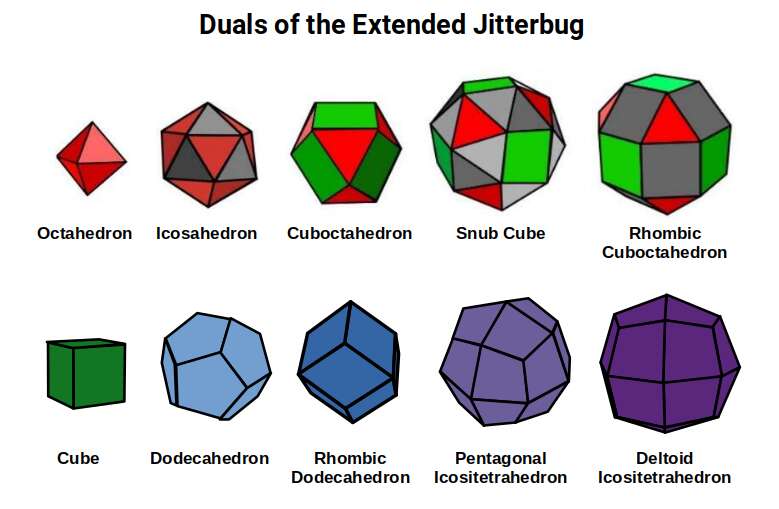
Whilst the notion of the jitterbug is relatively well documented through the work of Buckminster Fuller, what is not so commonly recognised is that the sequence can be extended to incorporate two more solids, the Snub Cube, and Rhombic Dodecahedron. We call this sequence the ‘Extended Jitterbug’.
The Extended Jitterbug is formed of 5 polyhedra, with the Cuboctahedron at its centre. The Rhombic Cuboctahedron is the largest of the group. We can see that both of the solids that we ascribed to the D-orbital sets can be transformed from one to the other through the Snub Cube. The Cuboctahedron can collapse into the Icosahedron, which is similarly to the Rhombic Cuboctahedron, in that it has a mid-section that can be rotated. Finally, the Octahedron is the smallest of the set, that Atomic Geometry represents as the P-orbital sets.
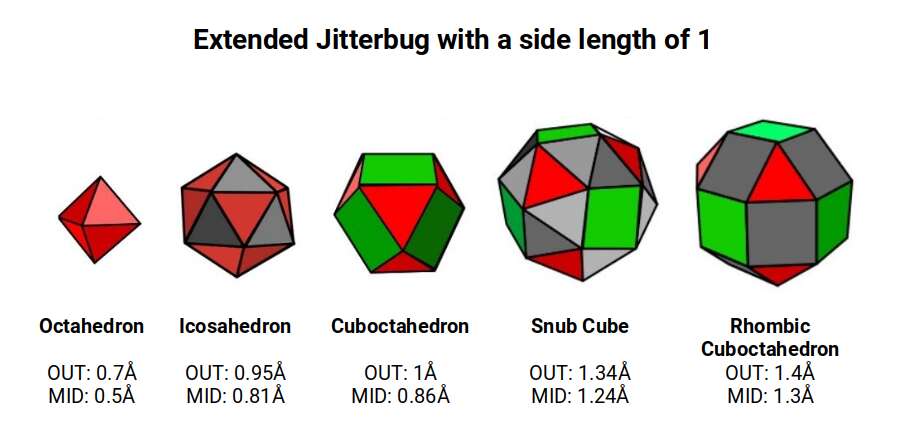
Whilst the model of the Extended Jitterbug can provide an interesting correlation to the geometric configuration of the D-orbitals, we can also find a striking resemblance to the atomic radii of many of the elements on the periodic table. Based on an Octahedron with a side of 1, as used in the pervious model, the expansion through the Jitterbug produces a Rhombic Cuboctahedron in the same proportion as the exploded model. As we have seen, the out and mid-sphere define the gap between the largest of the 1st P-orbital Elements and the smallest of the 2nd. Additionally, the Cuboctahedron can collapse to produce the Octahedron whose out and mid-sphere defines the radius of Carbon (6), 0.7Å, and Fluorine (9) 0.5Å.
This model reveals the second major radius found in the 1st D-orbital set, of 1.35Å. Except for the 1st element, Scandium (21), with a radius of around 1.6Å, all the other D-orbital elements in the 1st set exhibit a radius of either 1.4Å or 1.35Å, which turns out to be the out-sphere of the Snub Cube and Rhombic Cuboctahedron in the Extended Jitterbug model.
The radius of Carbon (6) 0.7Å, and Fluorine (9) 0.5Å from the 1st P-orbital set are found in the out and mid-sphere of the octahedron. The Cuboctahedron expresses the radii for Boron (5) 0.86Å, and 3 of the 2nd set of p-orbital elements, with a radius of 1Å. The out spheres of the Snub cube and Rhombic Cuboctahedron define two types of radii that are found in all but one of the 1st D-orbital elements. The mid-spheres define the radii of the first 2 elements on the next 3rd set of P-orbitals.
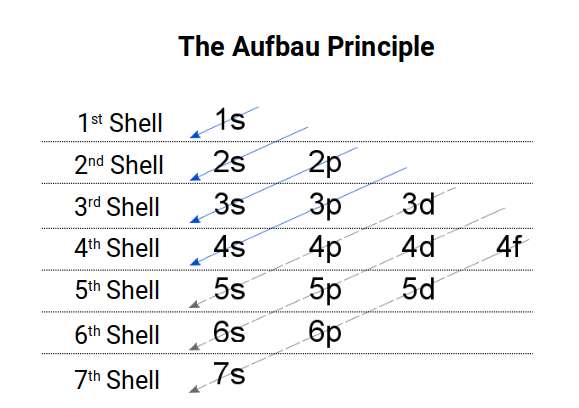
The Aufbau Anomalies
The order by which electrons fill the atomic structure is usually described by the Aufbau Principle. This is depicted as a set of diagonal lines across each shell denoting when each type of orbital appears. The diagonal through the first shell only passes through a single set of S orbitals. The next arrow also only passes through the S-orbitals of the second shell. The 3rd arrow defines the first P-orbital set, followed by a 3rd pair of S-orbital electrons. The 4th arrow repeats the same process for the 3rd and 4th shells. Only by the 5th arrow are the 1st D-orbitals created. Notice that the S-orbital electrons have already been formed in the shell above. Before the F-orbitals can form, a second round of S, P and D orbitals must complete. The F-orbitals appear on the 7th arrow, which only goes as far as halfway through the 6p orbitals before the radioactive elements begin.
Whilst this does provide a good overview of the atomic structure, there are a few exceptions. D-orbital elements exhibit strange anomalies as they form. Chromium (24), has only one S-orbital election in its outer shell, as its counterpart mysteriously appears as an extra D-orbital. This means that whilst the D-orbitals can form up to a set of 3, as found in Vanadium (23), the subsequent element will complete half of the D-orbitals set, thus avoiding a set of 4 D-orbitals in a single element. The same can be said of the second half of the D-orbital elements. Element 26, 27, and 28, form as would be expected. Then Copper (29) again appears with only a single S-orbital electron, and a full D-orbital configuration. This become more apparent when we examine the Electron configuration of the 1st D-orbital set in two halves. The first half produces orbitals formed of UP spin electrons, and the second half comprises DOWN spin electron that complete the set.
Up electrons
|
Element
|
D-orbital
|
S-orbital
|
Radius
|
|---|---|---|---|
|
Scandium (21)
|
1
|
2
|
1.6
|
|
Titanium (22)
|
2
|
2
|
1.4
|
|
Vanadium (23)
|
3
|
2
|
1.35
|
|
Chromium (24)
|
5
|
1
|
1.4
|
|
Maganese (25)
|
5
|
2
|
1.4
|
Down electrons
|
Element
|
D-orbital
|
S-orbital
|
Radius
|
|---|---|---|---|
|
Iron (26)
|
6
|
2
|
1.4
|
|
Cobalt (27)
|
7
|
2
|
1.35
|
|
Nickel (28)
|
8
|
2
|
1.35
|
|
Copper (29)
|
10
|
1
|
1.35
|
|
Zinc (30)
|
10
|
2
|
1.35
|
We can see that elements 24, 25, and 29, 30, exhibit the same number of D-orbitals. Each anomaly occurs at the same place in the formation of the up and down sets of electrons. This makes sense when the orbital types are divided into 3 cubic and 2 torus types. The first three D-orbitals form a cubic set on the x, y, and z axis either side of the P-orbital set. Once formed, the next element adds 2 D-orbitals to complete the torus set.
As the first 3 D-orbitals form, the radius of the atom reduces in size, to 1.35Å, which is the out-sphere of the Snub Cube. The 4th element, Chromium (24), only has a single S-orbital electron in its outer shell, and yet the radius increases to 1.4Å. Geometrically, the Snub Cube expands into the Rhombic Cuboctahedron, as the two torus D-orbitals complete the set. The Rhombic Cuboctahedron has 24 corners, which is the same number of protons found in the Chromium atom. If we include the number of neutrons, then the total number of nucleons is 52. This number is divisible by 13, which is the number of spheres that can be perfectly nested within a Cuboctahedron.
Again we find the same S-orbitals anomaly occurring with the second to last element of the set, Copper (29). When we examine the number of nucleons in the atomic centre, we find there are 29 protons and 36 neutrons, a total of 65. Just like the Chromium nucleus, this number is also divisible by 13. Therefore, in the 1st D-orbital set, the two atoms that exhibit anomalies in their electron configuration both have a nucleonic count that can be divided by 13, the number of spheres nested by a Cuboctahedron.
Nucleons and radius of the 1st D-orbital set
|
Element
|
Protons
|
Neutron
|
Nucleons
|
Divisor
|
Radius
|
|---|---|---|---|---|---|
|
Scandium
|
21
|
24
|
45
|
(3 x 13) +6
|
1.6
|
|
Titanium
|
22
|
26
|
48
|
(3 x 13) + 9
|
1.4
|
|
Vanadium
|
23
|
28
|
51
|
(3 x 13) +12
|
1.35
|
|
Chromium
|
24
|
28
|
52
|
4 x 13
|
1.4
|
|
Maganese
|
25
|
30
|
55
|
(4 x13) +3
|
1.4
|
|
Iron
|
26
|
30
|
56
|
(4 x 13 ) +4
|
1.4
|
|
Colbalt
|
27
|
32
|
59
|
(4 x 13) + 7
|
1.35
|
|
Nickel
|
28
|
30
|
58
|
(4 x 13) +6
|
1.35
|
|
Copper
|
29
|
36
|
65
|
5 x 13
|
1.35
|
|
Zinc
|
30
|
35
|
65
|
5 x 13
|
1.35
|
This is a completely new perspective which resolves the strange occurrence of the Aufbau Anomalies, not through mysterious electromagnetic interactions and ‘shielding’ as is commonly taught. Instead, we find that the solution is purely geometric in nature.
Evidence to support this claim comes from the examination of the atomic nucleus. All the elements between these two anomalous atoms exhibit a neutron count of 30, with one exception, Cobalt (27) which has 32. After Nickel (28) with 58 nucleons, the anomalous element, Copper (29), appears with 65 neutrons. This large jump in the size of the nucleus is not matched by an increase in radius. Instead, the atom remains at a consistent size of 1.35Å, a fact that cannot be accommodated very easily through conventional theory.
nucelar Geometry
In the theory of Atomic Geometry, the Nucleus of an atom plays an important role in explaining the different types of qualities expressed by a particular element. Geo-nuclear Physics is the name of the subdiscipline that focuses particularly on the number of Neutrons and Protons which constitute a stable atom. As we can see, at the number of Nucleons, and the ratio between protons and neutron seems to vary widely across different elements. Generally, the higher the atomic number, the more neutrons are needed to maintain a stable atomic structure.
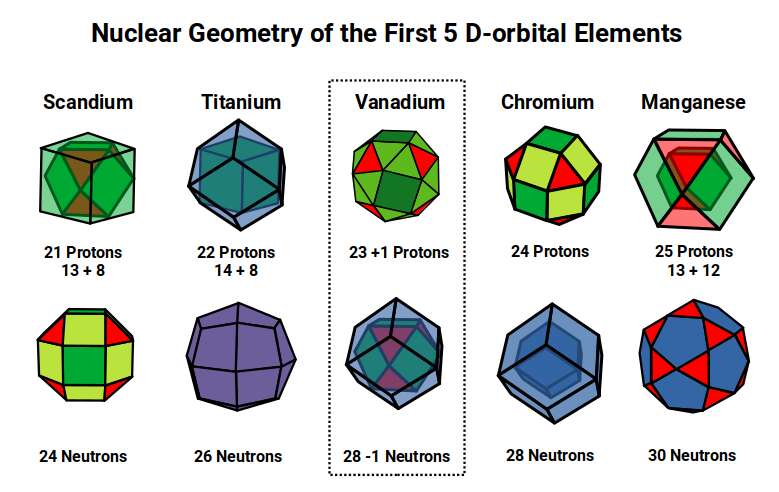
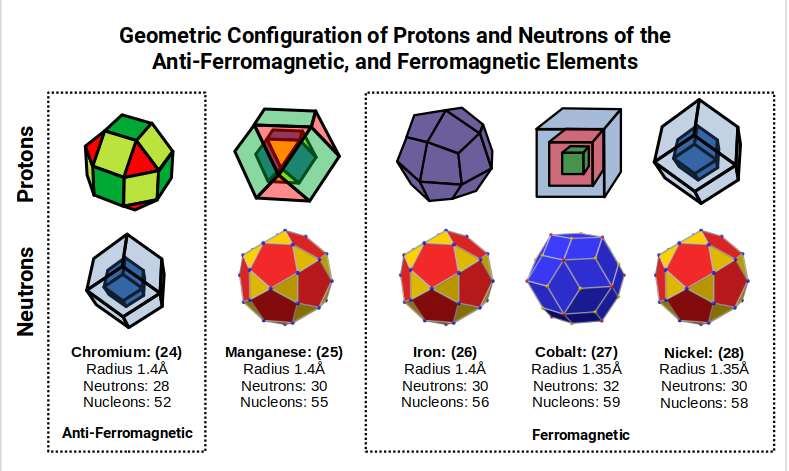
Scandium (21) exhibits the largest radii of any D-orbital Element of 1.6Å, a value close to the Golden Ratio (Φ), or 1.618. This larger size is due to the fact that the D-orbitals have only just started to form, and so the radius is being reduced in size from the even larger pair of S-orbital Elements, Potassium (19) and Calcium (20) with radii of 2.2Å and 1.8Å, which we will explain in more detail shortly.
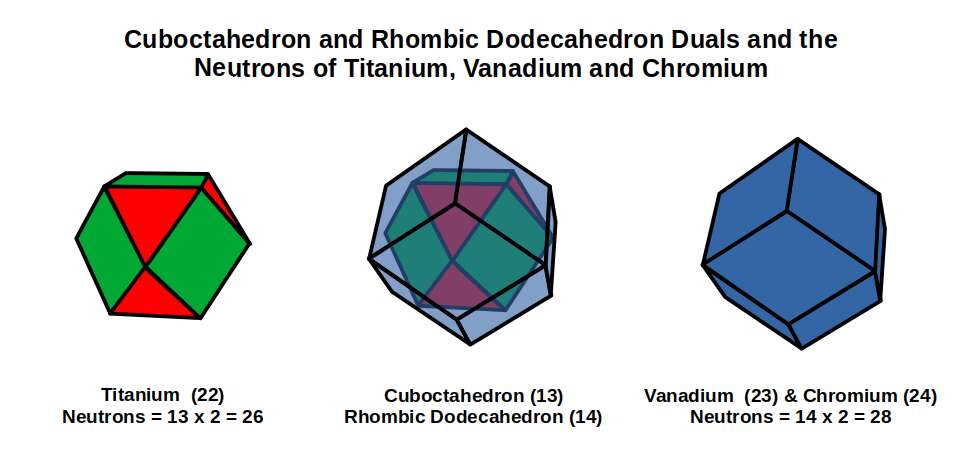
After this, the radii for the next 2 element drops to 1.4Å, Titanium (22), which is stable with 26 neutrons. A Cuboctahedron can nest 13 spheres perfectly in space, with 12 surrounding 1 at the centre, As 26 is 2 x13, we find the number of neutrons is equal to the number of spheres nested by 2 Cuboctahedra. Additionally, the 26 neutrons, bring the total number of nucleons to 48, which is the number of corners found in 2 Rhombic Cuboctahedra. Thus, the Nucleus of Titanium (22) is a perfect match for our geometric model.
The subsequent element, Vanadium (23), exhibits a slightly smaller radius of 1.35Å. At this point, there are 3 D-orbital electrons, which is enough to complete a Cuboctahedron. Yet for the next element, Chromium (24), the radius increases again, moving back up to 1.4Å. When we examine the nucleus of these 2 elements, we find both have 28 Neutrons. This number is divisible by 14, which is the number of corners of a Rhombic Dodecahedron. Geometrically, we can see that neutrons of Titanium (22) exhibits a Cuboctahedral structure, which morphs into it duel for Vanadium (23), and Chromium (24).
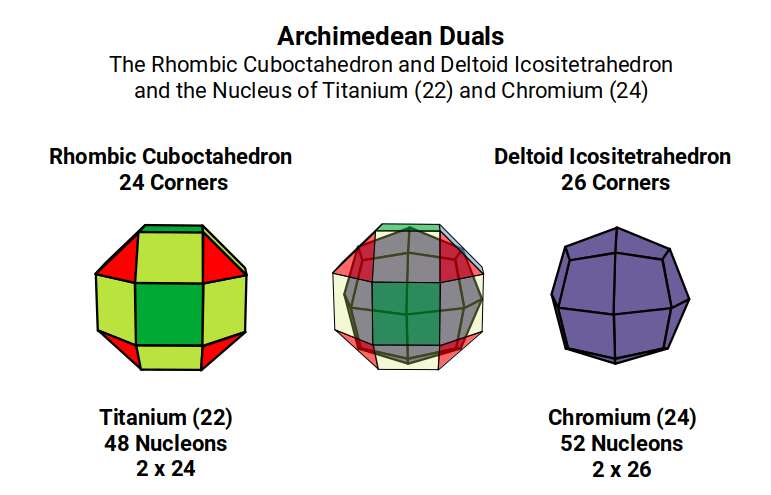
When we count the total number of nucleons for Vanadium (23) and Chromium (24), the total is 51, and 52, respectively. As number 52 is 4×13, we can see that geometrically, the Chromium (24) Nucleus forms 4 Cuboctahedra, which actually translates into the corners 26 of 2 Deltoid Icositetrahedra, (the Dual of the Rhombic Cuboctahedron). From Titanium (22) to Chromium (24) the shape of the nucleus transforms to its dual.
The transition from Titanium (22) to Chromium (24) shows a transformation of geometric structure from the Cuboctahedron and Rhombic Cuboctahedron, and their dual. Between these elements, Vanadium (23) exhibits a slightly reduced radius, falling from 1.4Å to 1.35Å, that occurs as this transition takes place. When we examine the difference between Vanadium (23) and Chromium (24), both exhibit the same number of Neutrons, but differ in their Proton count by 1. This means both exhibit the same geometry in terms of neutrons, which equates to the 14 corners of 2 Rhombic Dodecahedra. However, the difference in protons, produces a slightly different geometry for the overall nucleon count.
If 28 of the Neutrons of Vanadium (23) go towards forming a Rhombic Dodecahedron, there are only 23 protons, one less than is needed to form a Rhombic Cuboctahedron. Therefore, 1 neutron must be added to the proton count to produce the form. This leaves 27 neutrons, which is formed by a combination of a Cuboctahedron (13 corners), and Rhombic Dodecahedron (14 corners), i.e. a nested set of duals. The number 27 also equates to the number of units in a Cube with a side of 3.
The reason for the slight dip in the radius of Vanadium (23) can therefore be attributed to the fact that 23 is an odd number, which means there are not quite enough protons to complete the Rhombic Cuboctahedron. Thus, it collapses into the Snub Cube. This is easier to comprehend once we examine the nucleon count in terms of multiples of 12 and 13. Titanium (22) has 12 x 4 Nucleons, which is the number of corners in 4 Cuboctahedra. Inside a Cuboctahedron is a space where another sphere can be placed, bringing the total to 13. Chromium (24) has 52 Nucleons (13 x4), which fills in the missing space at the centre of each of the 4 Cuboctahedra. Vanadium (23), which appears in between these elements, can only fill 3 of the spaces inside a Cuboctahedron, leaving the 4th empty. This causes a collapse in the geometric structure, into the Snub Cube, which is the reason why the radius of Vanadium (23) becomes reduced to 1.35Å, just before the Rhombic Cuboctahedron competes With Chromium (24).
|
Element
|
Protons
|
Neutrons
|
Neucleons
|
Cuboctahedra
|
Radius
|
|---|---|---|---|---|---|
|
Titanium
|
22
|
26
|
48
|
12 + 12 + 12 + 12
|
1.4Å
|
|
Vanadium
|
23
|
28
|
51
|
13 + 13 + 13 + 12
|
1.35Å
|
|
Chromium
|
24
|
28
|
52
|
13 + 13 + 13 +13
|
1.4Å
|
Chromium (24) exhibits 24 Protons and 28 Neutrons, which is the prefect ratio to form the 24 corners of a Rhombic Cuboctahedron, and 2 Rhombic Dodecahedra. At this point, the D-orbital set suddenly completes, creating the 1st Aufbau Anomaly.
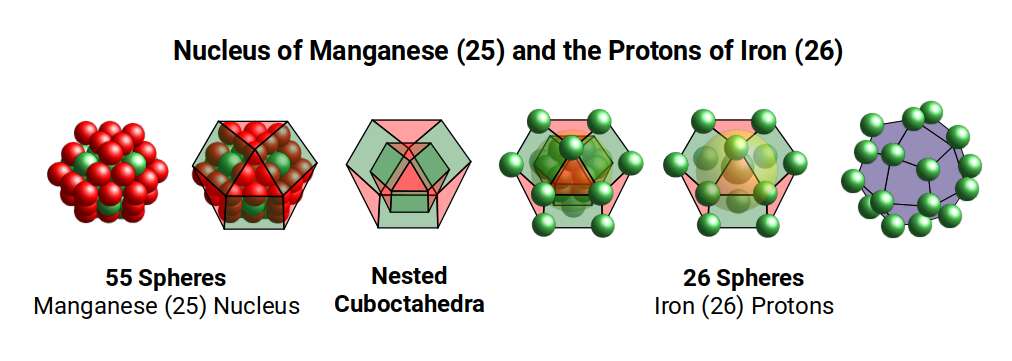
After this, Manganese (25) forms, marking the halfway point in the D-orbital formation with 55 Nucleons. Just as a Cube can be formed of 8 (2³) and 27 (3³) units, so a Cuboctahedron expands from 13 to 55 units. These are call Cuboctahedral numbers, which are also applicable to the Icosahedron, and is recognised as being a magic number, in Chemistry and nuclear Physics.
When we consider these first 5 elements, we can see the at each step the nucleus is transforming through a geometric process. Beginning with Scandium (21) with a neutron count of 24, which are the corners of Rhombic Cuboctahedron, subsequent elements transform through geometry. The 26 Neutrons of Titanium (22), form the corners of its dual, the Deltoid Icositetrahedron, after which the next 2 element both express 28 neutrons, which divides into 2 Rhombic Dodecahedra, as the proton count reaches 24, and the Rhombic Cuboctahedron forms.
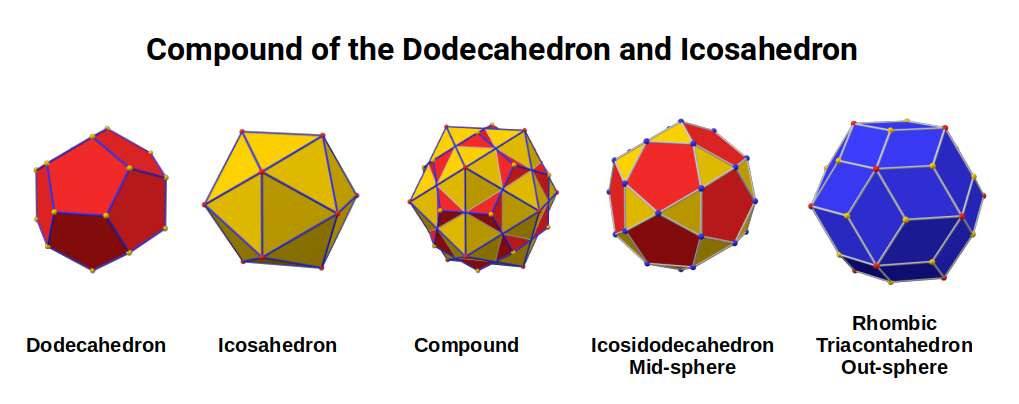
Finally, this combines into a larger Cuboctahedron, with the magic number 55 forming the Manganese Nucleus. The number of Neutrons increases to 30, which is the same for Iron (26), and Nickel (28). We ascribe this to the 30 corners of the Icosidodecahedron, which is produced from the mid-sphere of a compound of a Dodecahedron and Icosahedron. This is an important solid in the transition from a 4D to 5D hypercube, which we examine in more detail shortly.
The 25 Protons are formed of a set of 13 and 12, which completes the spheres nested in a Cuboctahedron, and the 12 corners of the larger one, into which the neutrons 30 can fill in the remaining spaces. This examination of these first 5 elements therefore shows a transition from Scandium (21), with protons formed of a Cuboctahedron and Cube (13+8 protons) and comprised of 24 neutrons in the form of a Rhombic Cuboctahedron, up to a Large Cuboctahedral structure made of 55 Nucleons.
After Manganese, (25) the next element, Iron, has the same number of neutrons, but 26 protons, which is 2×13 or the number of corners formed from a Deltoid Icositetrahedron. Notice that this is the same numbers at the neutrons in titanium (22), which is also ascribed the same geometry. This is the final D-orbital element in this set, with a radius of 1.4Å.
After Iron, (26), the radius collapses to 1.35Å for Cobalt (27). The 27 protons form a Cube with a side length of 3, just like the neutrons of Vanadium (23). The neutron count for Cobalt (27) increases from 30 to 32, which we ascribe to the corners of the dual of the Icosidodecahedron, the Rhombic Triacontahedron. This produces the template for the 6D hypercube, in the same way the Rhombic Dodecahedron produces the template for the Tesseract. Therefore, as the neutrons changes geometry, we find that the electron cloud radius collapses into the Snub Cube.
Nickel has 28 Protons, the same number as the Neutron count of Vanadium (23), and Chromium (24). This is depicted as 2 nested Rhombic Dododecahedra. Once the number of protons passes 27, forming the Hypercubic structure, the protons divide into 2 nested solids, at which point the number of Neutrons suddenly drops to 30. Presently, there is no explanation as to why Nickel (28) should exhibit 2 fewer neutrons than Cobalt (27), yet exhibit exactly the same radius. However, geometrically, we can see that this represents the collapse Rhombic Icosidodecahedron, (the 6D hypercube), back into is Dual, the Icosidodecahedron, as we pass the number 27.
These 3 elements are the only ones on the periodic table to exhibit ferromagnetic qualities at room temperature. After this, Copper (29), does not exhibit ferromagnetic properties, but is a good conductor of electricity. As electricity and magnetism lie at the foundations of all scientific thought, including light, energy, and matter, the realisation that these two fundamental forces are express within this small group of elements, is highly significant. We will examine these atoms in greater detail shortly.
The number of neutrons in the final 2 elements increases dramatically. The Pentagonal Icositetrahedron is the Dual of the Snub Cube and has 38 corners. If we ascribe this solid to 29 protons of Copper, then an extra 9 neutrons must be added to complete the form. Copper actually comes in 2 forms, one with 34 neutrons, and another with 36, that appear roughly in a 70% to 30% ratio respectively. These are called Isotopes. This produces about an average of 35 Neutrons. When we subtract the 38 nucleons that complete the corners of the Pentagonal Icosidodecahedron, the remaining neutrons will be 25 or 27, with an average of 26. This reflects in the geometries of the Proton count of Chromium (25), Iron (26), and Cobalt (27).
|
Protons
|
Neutrons
|
Neucleons
|
- Pent. Icosidodec. (38)
|
Neuclon Remainder
|
|---|---|---|---|---|
|
29
|
34
|
63
|
25
|
13 + 12
|
|
29
|
35
|
64
|
26
|
13 + 13
|
|
29
|
36
|
65
|
27
|
13 + 14
|
Yellow row represent the average nucleon count between the 2 stable isotopes of Copper
The Final Element, Zinc (30), exhibits the same number of Protons as the Neutron count of Chromium (25), Iron (26), and Nickel (28), represented by the Icosidodecahedron. This element exhibits 3 main isotopes with neutron counts of 34, 36, and 38. Again we can subtract 38, the number of corners for the Pentagonal Icositetrahedron, which produces a remainder of 26, 28, and 30.
|
Protons
|
Neutrons
|
Neucleons
|
- Pent. Icosidodec. (38)
|
Neuclon Remiander
|
|---|---|---|---|---|
|
30
|
34
|
64
|
26
|
13 + 13
|
|
30
|
36
|
66
|
28
|
14 + 14
|
|
30
|
38
|
68
|
30
|
|
Yellow row represent the average nucleon count between the 3 Main stable isotopes of Zinc
Notice that the last isotope produces the perfect division between 30 Protons and 38 Neutrons, creating a geometric structure formed of the Pentagonal Icositetrahedron and Icosidodecahedron. After this, the D-orbital elements complete and the P-orbitals begin. When we compare the 1st and 2nd half of this D-orbital set, we find that the neutrons in the first half tend to transform into the proton count in the 2nd half, as the geometry of the nucleus evolves.
The Rhombic Cuboctahedron and the Snub Cube
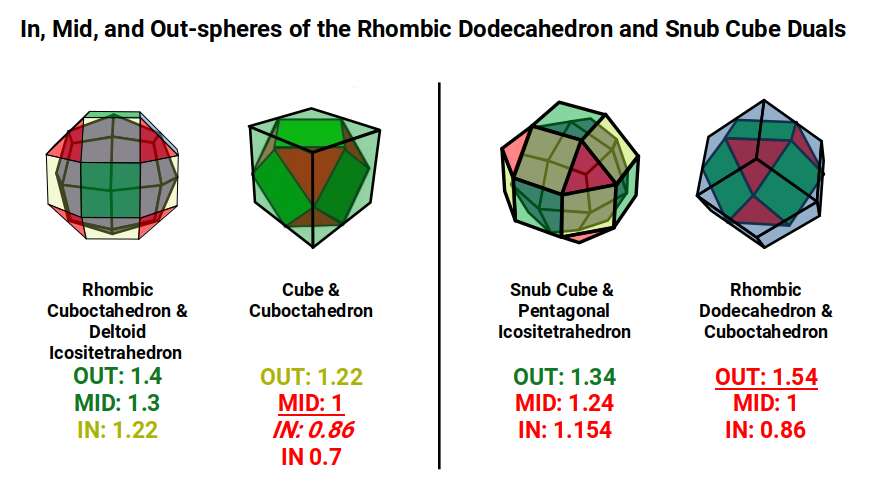
After Iron (26), the remaining D-orbital elements in the 1st set all express the same radius of 1.35Å. This shift is represented geometrically as the collapse of the Rhombic Cuboctahedron into the Snub Cube, as part of the Extended Jitterbug transformation into the Cuboctahedron.
When the Rhombic Cuboctahedron creates a nested set with its dual, the Deltoid Icositetrahedron, that produces an in, mid and out-sphere. The same can be said of the Snub cube and its dual, the Pentagonal Icositetrahedron. When we examine the radius of each set, we find a strong correlation to many of the atomic radii.
Set to a relative side length of 1, the out-spheres of both sets, defines the 2 main types of atomic radii found in the 1st D-orbital set. The In-sphere of the Rhombic Cuboctahedral pair exhibits a radius of 1.22Å, which approximates that of Helium (2), defining the size of the 1st atomic shell. This is also the out-sphere of the √2 Cube, found previously in our geometric model of the D-orbitals, which has a mid-sphere of 1Å. This matches the radius of 3 P-orbital elements, Phosphorus (15), Sulphur (16), and Chlorine (17), that in the same shell as this D-orbital set.
When the Rhombic Cuboctahedron collapses into the Snub cube, all the out, mid, and in-spheres are also reduced in size. The out-sphere now equals 1.35Å, the second main D-orbital radius. The mid-sphere radius drops from 1.3Å to 1.24Å, which in turn produces a smaller in-sphere radius of 1.154Å. The series is an exact match for the 3rd set of P-orbital radii that form directly after the 1st D-orbital set. This set begins with Gallium (31), with a radius of 1.3Å, followed by Germanium (32), radius 1.25Å. Just like the previous P-orbital set, the next 3 elements, Arsenic (33), Selenium (34), and Bromine (35), all exhibit a radius of 1.154Å. The uniform nature of these orbital elements and those of the previous P-orbital set is not predicted or even explained by the standard model.
Yellow = S-orbital Radii – Red: P-orbital Radius – Green = D-orbital Radii
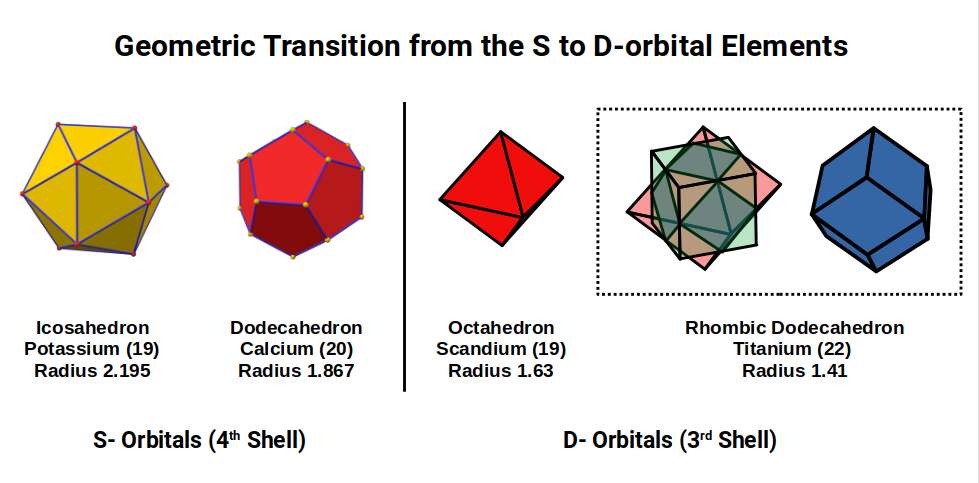
The transition of the P-orbitals, from 1Å (3rd shell) to 1.154Å (4th shell), offers a geometric explanation for the radii of the first set of D-orbital elements, which appear after 2 S-orbitals, (element 19 and 20), form in the 4th Shell above. Potassium (19) has an extremely large radius of 2.2Å, which is over twice the size of the 1Å elements that form previously. The reason for this large jump in atomic radii is not deeply understood. However, an Octahedron can nest a Cuboctahedron perfectly in its mid-sphere. If the Cuboctahedron has a side of 1.154, the side of the Octahedron that encompasses it will be doubled to 2.3Å. This will produce an out-sphere of 1.63Å, which is roughly the radius of the 1st D-orbital element, Scandium (21).
This Octahedron can be expanded through the Jitterbug Transformation, to create an Icosahedron which has an Outsphere of 2.195Å and mid-sphere of 1.86Å, the radius of the 2 S-orbital Elements. Therefore, we can see that the large jump between the P-orbital elements in the 3rd shell, to the S-orbitals that form afterwards in the 4th Shell are based in the difference of radii from 1Å to 1.154Å. When the Icosahedral S-orbital form in the 4th shell, each subsequently falls from the out-sphere, into the mid-sphere, which, is a transformation of the Icosahedron into its Dual the Dodecahedron. After this the structure collapses into an Octahedron forming the radius of the first D-orbital Element in the 3rd shell. As the D-orbitals form, the Octahedron gets reduced to a side length of 2, which, when compounded with the √2 Cube, creates the template for the Rhombic Dodecahedron, found in the structure of the Titanium (22) Nucleus.
Note: the 3rd shell geometries are formed with a side length of 1, whereas the 4th shell exhibits a side of 4÷√3.
After Titanium (22), the radius of the atom collapses for the first time to 1.35Å for Vanadium (23). The neutron count changes from 26 to 28, however as 23 is an odd number, one neutron goes towards completing the 24 points of the Snub Cube, leaving 27 neutrons to form a Cuboctahedron and Rhombic Dodecahedron. As these are Dual Polyhedra, they can be compounded so that the sides of the Rhombic Dodecahedron divides the sides of the Cuboctahedron through the mid-point. When the corners are connected, it forms a new solid with 26 corners inside which another sphere can be nested, bringing the total up to 27.
A second polyhedron is formed by removing the corner caps, which produces a shape with 24 corners, resembling the Rhombic Cuboctahedron. Thus combined both solids exhibit 50 corners, which, if we include the central sphere, equals 51, the number of neutron found in Vanadium (23). With has a radius of 1.35Å, it appears just before the Rhombic Cuboctahedron Completes, with chromium (24).
After this, the radius of the atom stabilises at 1.4Å, for elements 24, 25, and 26. Then element 27, Cobalt, produces the second drop in radius. When we compare Vanadium (23), and Cobalt (27), which are the 1st two elements in the set with a radius of 1.35Å, we notice that the number 27 appears in both structures. As pointed out previously, this is a cubic number (3³), however, it can also be ascribed to the corners of a Cuboctahedron and Rhombic Dodecahedron pair (13 +14), which when compound creates the solids depicted previously. This increases the out-sphere 1 to 1.154 which is found as the radius of the in-sphere of the Snub Cube, which collapses the radius to 1.35Å. Subsequent element maintain this same radius as once formed this new in-sphere of 1.154, takes precedence, as the D-orbitals complete, before collapsing into the subsequent P-orbitals based on the same radius.
Ferromagnetism and the Golden Ratio
Previously, we saw how the protons of Chromium (24) complete the Rhombic Cuboctahedron. This element has a Neutron count of 28, which forms a nested pair of Rhombic Dodecahedra. At this point, the D-orbitals complete prematurely, creating the 1st Aufbau Anomaly. After this, there is an increase in the number of Neutrons to 30. Out of the next 4 elements, 3 exhibit this same number of neutrons, except Cobalt (27) which has 32.
|
Element
|
Protons
|
Neutron
|
Nucleons
|
Radius
|
|---|---|---|---|---|
|
Maganese
|
25
|
30
|
55
|
1.4
|
|
Iron
|
26
|
30
|
56
|
1.4
|
|
Colbalt
|
27
|
32
|
59
|
1.35
|
|
Nickel
|
28
|
30
|
58
|
1.35
|
Previously, we ascribed these two types of neutron count to the corners of the Icosidodecahedron and Rhombic Triacontahedron. These solids are duals of each other and are derived from the compound of an Icosahedron and Dodecahedron. By removing the corner caps, the Icosidodecahedron can be found, whereas joining the corner of both solids forms the Rhombic faces of the Triacontahedron.
The transition from 28 to 30 neutrons occurs from Chromium (24) to Manganese (25). Geometrically, 2 Rhombic Dodecahedra transform into a single Icosidodecahedron. Previously, we saw how the out-sphere of the Cuboctahedron increases from 1 to 1.154, which determine the difference in radii from the 2nd and 3rd P-orbital sets. This transformation contains a little known correlation to the Icosahedron, and Dodecahedron. If a Cuboctahedron with a side of 1.154 collapses into an Icosahedron, it produces a smaller out-sphere of about 1.1Å, and a mid-sphere of 0.934Å. This can be compounded with a Dodecahedron, which has an out-sphere of 1Å, the average size of the 2nd P-orbital set, which is also the mid-sphere of the Cuboctahedron. By connecting the corners of both solids, the Rhombic Triacontahedron forms, also with an out-sphere of 1.1Å, the same size as the Icosahedron. By removing the corner caps, the Icosidodecahedron is created. This will have an in-sphere of 1Å, which places the corners of the Dodecahedron at the centre of each of its triangular faces. This provides a geometric mechanism by with the 28 Neutrons of Chromium (24) can increase to 30 for Manganese (25).
Manganese (25) has a total of 55 Nucleons, which is the exact number needed to form a larger Cuboctahedron. As the number of Protons increases to 26 for Iron, so the Cuboctahedron can be divided into 2, each containing the 2 sets of 13. Thus, the radius of the atom is maintained at 1.4Å. Both elements exhibit 30 Neutrons, however, as the Cuboctahedron begins to divide, so a new geometry can be formed. The Deltoid Icositetrahedron has 26 corners, and is the duel of the Rhombic Dodecahedron. Thus, the outer shell shifts from the Rhombic Cuboctahedron with 24 corners, which defines protons of the Chromium (24), into is dual with 26 corners, as it transitions through the large Cuboctahedral structure formed by Manganese (25).
The subsequent element, Cobalt, has 27 protons, and 32 neutrons. Just as Manganese (25) forms a larger Cuboctahedron, 27 spheres can be placed into a larger Cube with a side of 3. At the centre of the structure sits a single sphere, surrounded by 26 others, which divides the structure into two, just like the projection of 4D hypercube. However, what is not so apparent is that the Cube with a side of 2 can also be placed in the middle of the other 2 cubes. As 2 is an even number, this cube is not directly defined by the spheres of the odd number cubes. Instead, it resides in the ‘reciprocal space’, between spheres. When we consider this structure of 3 nested Cubes, we find that it resembles the shadow projection of a 5D hypercube. Additionally, we find the 5D cube has 32 corners, which is the same as the number of corners found in the Rhombic Triacontahedron, and the number of neutrons in the Cobalt Atom.
Notice the hexagonal cell that forms at the centre of the rotating 5D cube, indicative of its HCP crystal structure of Cobalt, Whereas the previous 4 elements all form BCC structures, and the subsequent 2 elements all form FCC Structures.
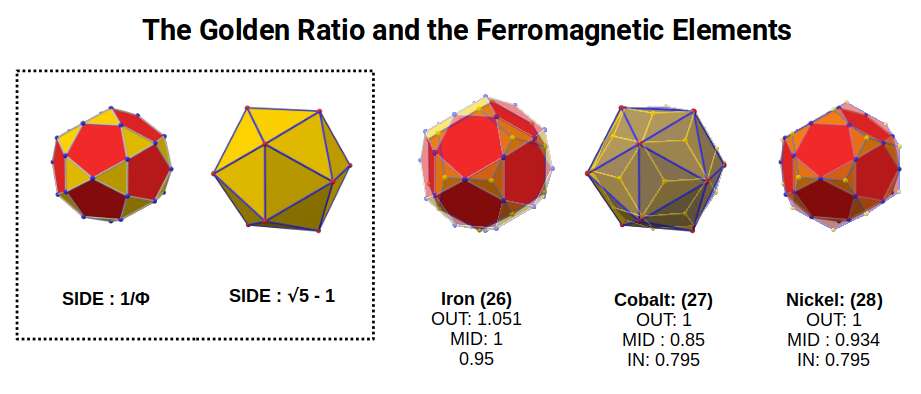
Iron (26) is by far the most ferromagnetic elements on the periodic table. This is followed by Cobalt (27) and Nickel (28), which together form the only elements that exhibit ferromagnetic qualities at room temperature. When we examine the transformation of the elements, we can see that as the elements transition from Iron to Cobalt, the radius drops from 1.4Å to 1.35Å, which is indicative of a shift in geometry from the Rhombic Cuboctahedral Duals, to the Snub Cube Duels. As noted previously, this arises from the shift of a Cuboctahedron, side 1Å, to a Cuboctahedron, side 1.154Å. This transformation is geometrically represented as the Cuboctahedron, collapses into an Icosahedron/Dodecahedron to maintain an out-sphere of 1. As this occurs, there is a point between the transition, where the side-length of the Icosahedron becomes equal to √5-1, which is 2x 1÷Φ, the Golden Ratio. This produces a side length for the Icosidodecahedron of 1÷Φ.
The mid-sphere of the construction is now equal to 1, which is also the out-sphere of the Icosidodecahedron. We can apply this construct to the nucleus of Iron. When the radius drop to 1.35Å, we find the Rhombic Triacontahedron forms also with an out-sphere of 1. As the mid-sphere of 1 transition to an out-sphere of 1, so we find there is a collapse in the radius of the atom. Nickel exhibits the same number of neutrons (geometry) as Iron, however this time the out-sphere of the Icosidodecahedron becomes 1, which unifies with the Icosahedron with a side of 1.154.
The Golden Ratio is naturally inherent in this geometric structure, as it can be easily derived from the pentagon. In the case of Iron, the Icosidodecahedron also exhibits a side of 1÷Φ. This produces geometric correlation that can be mapped to much higher geometric dimensions. One key example is the famous E8 Geometry, from which the Icosidodecahedron can be extracted. This begins to provide us with a geometric solution to the extremely high level of ferromagnetic properties ascribed to the Iron Atom. Rather than the electron configuration, it suggests the real reason lies in the fact the neutrons exhibits the Golden Ratio found in the side lengths of the Icosidodecahedron, and the protons form the Deltoid Icositetrahedron, which we explore in greater detail in our post that examines the geometric nature of the ferromagnetic and electrically conductive fields.
Traditional theory suggest that the reason for the ferromagnetic qualities of Iron, Cobalt, and Nickel is due to the fact that these atoms exhibit large numbers of unpaired D-orbital electrons. However, Chromium (24) exhibits even more unpaired electrons and is anti-ferromagnetic, meaning it resists change in a magnetic field. Manganese (25) also exhibits many unpaired electrons yet does not exhibit any kind of ferromagnetic properties. The same can be said of all other D-orbital elements, even those in higher shells with have that same number of unpaired electron as Iron, Cobalt, and Nickel. It is worth noting that one other element, Gadolinium, is known for is ferromagnetic properties, although it has a tendency to lose its magnetic domains at room temperature. This element has 64 protons, which is also a cubic number, 4³.
We can now review the geometric transformation of the D-orbital elements from Chromium (24), with its antiferromagnetic qualities, into the ferromagnetic elements. As Iron (26) is by far the most Ferromagnetic element, we can see that the transition between the 2 opposite types of properties is separated by Manganese, with its large Cuboctahedral structure. This transition changes the proton structure from the Rhombic Cuboctahedron, into its Duel.
The fundamental difference between ferromagnetic and antiferromagnetic, is to do with the ‘north/south’ orientation of the electron spin within a compound. Chromium will always alternate between the two types of orientation, whereas the ferromagnetic qualities of Iron are due to the north-south being orientated in the same direction. When we consider the atom as a 4D structure, we can attribute this behaviour to the nature of 4D rotation, which we suggest is the reason why the electrons can only exhibit either an UP or DOWN spin.
As Chromium completes the Rhombic Cuboctahedral structure, this 4D rotation will unify in alternating up and down orientation, which produces its anti-ferromagnetic qualities. Iron, on the other hand, exhibits the Duel of the Rhombic Cuboctahedron, and so exhibits exactly the opposite behaviour, where the atoms in the compound unify over large areas of the compound, termed magnetic domains.
As Cobalt forms, the radius of the atom decreases, along with the ferromagnetic properties of the atom, a trend that continues up to Nickel. All of these elements express either 30 or 32 neutrons, which is ascribed to the Icosidodecahedron, or Rhombic Triacontahedron respectively. Consequently, they inherit higher ‘dimensionality’, that we will explore in more detail at the end of this article.
The reason Manganese, with the same neutron structure, does not exhibit ferromagnetic qualities is due to the fact that a Cuboctahedron can nest spheres perfectly in space, which prevents the field from accumulating throughout a compound of this type. In simple terms, the Rhombic Cuboctahedron, and Cuboctahedron, are able to produce a uniform Honeycomb, whilst the Deltoid and Pentagonal Icositetrahedron, and Snub Cube cannot.
The lattice structures of elements is an expansive field of interest in Sold State physics and material science, which goes well beyond this simplified description. Often, elements that do not normally exhibit any kind of ferromagnetic or conductive nature as uniform compounds, can suddenly begin to express these properties in structures that contain a combination of more than one type of atom, as it normally the case in nature.
However, as a generalisation, this model offers a geometric explanation for the ferromagnetic, (and antiferromagnetic), properties of these elements, that explains why these atoms behave the way they do, and why other atoms that, according to present theory, should be magnetic are not.
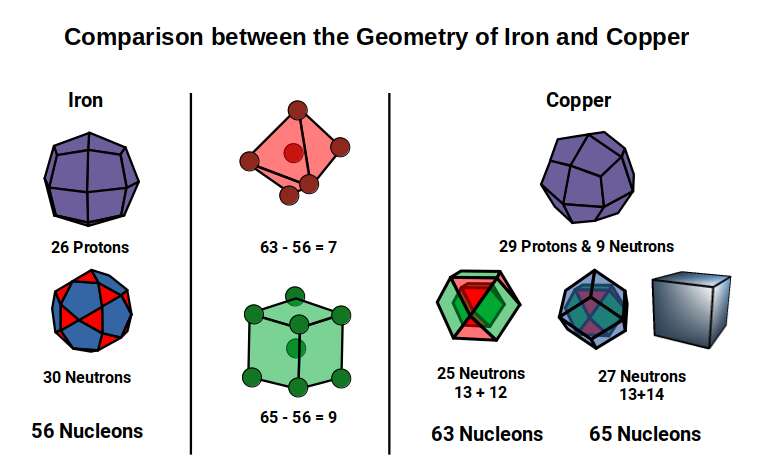
Copper and conductivity
The final 4 elements of the D-orbital set all have the same radius of 1.35Å. From this set, the first two, Cobalt (27) and Nickel (28), both exhibit ferromagnetic qualities. From Nickel (28) to Copper (29) there is a large jump in the total number of neutrons. As noted previously, final pair of elements also exhibit a larger number of isotopes. Copper (29) comes in 2 forms, with 63 or 65 nucleons, which produces an average of roughly 64, which is a Cubic number. Zinc (30) exhibit 3 main isotopes, that range from 64 to 68 nucleons.
|
Element
|
Protons
|
Neutron
|
Nucleons
|
Radius
|
|---|---|---|---|---|
|
Colbalt
|
27
|
32
|
59
|
1.35
|
|
Nickel
|
28
|
30
|
58
|
1.35
|
|
Copper
|
29
|
34-36
|
63 - 65
|
1.35
|
|
Zinc
|
30
|
34-36-38
|
64-66-68
|
1.35
|
Copper is the second most conductive element on the periodic table after Silver (47), although only be a small degree. The 3rd most conductive Element is Gold (79). Each appears in the same location in the 3 Stable D-orbital blocks, and exhibit only a single electron in their outer shell. Often, this single outer S-orbital is attributed as the reason for the conductive capacity nature of these atoms. However, as many other D-orbital elements also exhibit a single S-orbital Electron, (particularly in the 2nd D-orbital set), that do not produce conductive qualities to the same degree. A more complete solution is found in Bloch’s theorem, which examines the properties of conductivity from a wave perspective, rather than the electron particle model.
As noted previously, the Dual of the Snub Cube, the Pentagonal Icositetrahedron, exhibits 38 corners, due to the increase in the number of faces. If we subtract this from the total number of nucleons found in the copper isotopes, the result is 25 and 27, which is the proton count of Manganese and Cobalt.
As noted previously, Cuboctahedron has 12 corners, yet can nest 13 spheres in space. Therefore, 13+12=25 produces the geometry of two nested Cuboctahedra, the number of neutrons remaining once 38 is subtracted from the nucleons of the 1st isotope of Copper. As the 2nd isotope exhibit 2 more neutrons, this number increases to 27 which is the number of corners formed from a dual compound of a Cuboctahedron and Rhombic Dodecahedron. When we compare this geometric configuration to that of Iron, the most ferromagnetic element, we find the difference is 7 and 9 respectively. Geometrical 7 form the corners of an octahedron, with an additional unit at the centre (6+1), and a body centred cube (8+1).
The Octahedron and Cube are both found within the construction of the Deltoid and Pentagonal Ichositetrahedron. As each transforms from its dual, so the Octahedron increases in size, pushing through the centre of the square faces of each solid on the x, y, and z axis, whist the 8 corners that defines the cube collapse, reducing it in size. This shift affects the overall structure of the Rhombic Cuboctahedral D-orbital model. In the Iron Atom, the Deltoid Icositetrahedron produces an in-sphere of 1.22Å, which is the out-sphere of the √2 Cube, whereas the Octahedron expands in size, producing an out-sphere of around √2Å, and a mid-sphere of 1Å, with a side length of 2. This produces the perfect relationship to produce a compound of the cube and Octahedron, which forms the Template of the Rhombic Dodecahedron.
The Pentagonal Icositetrahedron of the Copper atom has an out-sphere radius of 1.35Å, which reduces the size of the Octahedron, which now exhibits a smaller mid-sphere of 0.94Å. An Octahedron can have its corner caps removed by dividing its sides into 3, to create a Truncated Octahedron, which is an Archimedean Solid. This now produces an out-sphere of 1Å. The Dual of the Truncated Octahedron is the Tetrakis Hexahedron. When nested around the Truncated Octahedron, this also produces an out-sphere of 1.22Å, matching that of the √2 Cube.
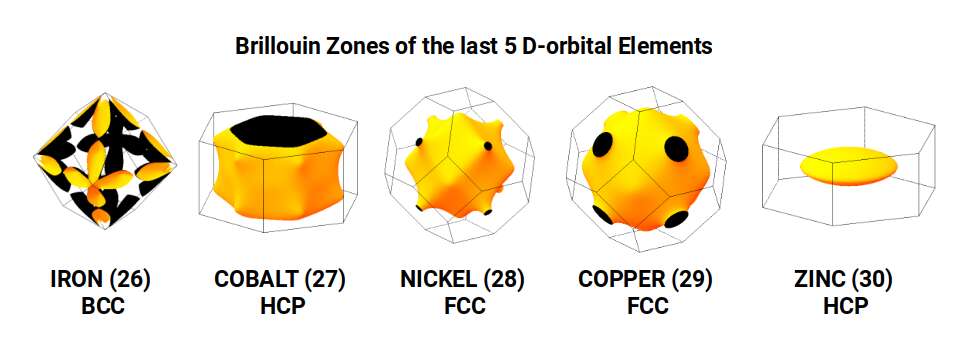
The Truncated Octahedron is recognised as an important polyhedron in the production of the conductive field in a material. These are called Brillouin Zones, which are derived from the ‘reciprocal’ space, sometimes termed k-space, of elemental compounds. Each element of the periodic table exhibits a different type of Brillouin Zone, which is partly dependent on the geometric structure of the compound’s crystal structure. For Iron, this is found to exhibit the shell of an Octahedron, whereas Copper, Silver, and Gold, all exhibit Truncated Octahedral zones. In solid-state physics, these are found to be the key reasons for the electromagnetic properties of different elements, which we cover in much greater detail in our post on the geometry of conducive and magnetic waves.
The nature of these Brillouin Zones is highly influenced by the type of lattice that a compound forms. These fall into 3 categories for the majority of all atoms. Iron Exhibits a Body Centre Cubic (BCC) formation, formed of 9 sites, where the 8 point form the corners of a Cube, with an additional point at its centre. Copper exhibits a Face Centred Cubic (FCC) formation which is similar, however the point at the centre is removed, and additional points are placed at the centre of each face, forming the nested structure of a Cube and Octahedron. The other types of crystal structure found in the D-orbital elements is the Hexagonal Close Packing (HCP) configuration, which is formed of hexagonal rings made of 7 points, which is indicative of the Cuboctahedron. When we compare these types of atomic crystalline structures to a 4D hypercube that passes through a 3D plain at through its various axes, as examined previously, we find that each produces a close match to the 3 different types.
This correlation between 3D and 4D space offers a unique perspective into the various structures formed through the crystal geometry of the D-orbital elements, as well as a wide variety of other stable elements found on the periodic table. This begins to produce a foundation which when explored in greater detail can offer new insight into the nature of the energetic structures produced from various compounds and solids.
Notice that the final element, Zinc (30), exhibits a HCP formation, which changes the shape of the Brillouin Zone, which is the main reason why is it not a particularly good conductor of electrical energy. Therefore, whilst both Copper and Zinc are attributed the same geometry of a Pentagonal Icositetrahedron, when the compound forms, the orientation of the 4D cube shifts, which in turn prevents the electron wave from propagating as effectively. Zinc has 30 Protons, which is the same number as the neutrons of Manganese, Iron, and Nickel, and is renowned for is ability to resist oxidisation. For this reason, it is often used to ‘galvanise‘ metal, to prevent it from rusting. It’s 3rd sable isotope has 30 protons and 38 Neutrons, which forms the corners of the Icosidodecahedron and Pentagonal Icositetrahedron, after which the D-orbital elements give way to the next set of P-orbitals.
The Compound of the extended Jitterbug
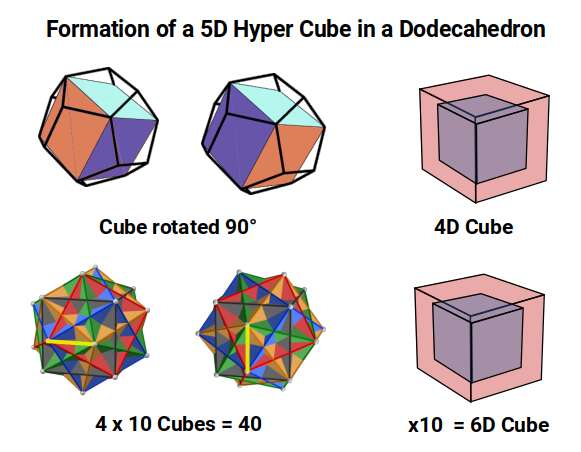
In this article we have examined the nature of the Atom is great detail based on the principles of geometry. At its heart lies the Extended Jitterbug, which produces the Rhombic Cuboctahedral model of 4D hypercubic space. Each of the 5 solids found in the Jitterbugs construction has a dual, which is always present at any stage. As the Rhombic Cuboctahedron completes with Chromium (24), so the Dual begins to emerge up to Iron (26), after which the radius of the atom collapses into the Snub Cube. As the D-orbitals begin to complete, so the Snub Cube gives way to its dual, for the final 2 D-orbital elements, after which the next P-orbitals begin to form. When we examine the duals of the Extended Jitterbug geometries, we find the Cuboctahedron transforms into the Rhombic Dodecahedron, which is the template for 4D hypercubic space. This is formed from a compound of a Cube and Octahedron, which are also duals of each other, and appear at the beginning of the construct. The Icosahedron and Dodecahedron duels are also present, which produces a total of 10 different polyhedra in the set.
As we have seen, these duals can be compounded to create a set of solids, formed from the out and mid-sphere intersection. In the example of the Cube and Octahedron, the compound creates a Rhombic Dodecahedron from the unification of the corners of the 2 solids. If we remove the corner caps, it creates the Cuboctahedron. Therefore, these duels appear at the start of the jitterbug transformation, as well as at the centre of the set.
When we examine the full set, we find that many of the geometries ascribed to the D-orbital elements. Icosahedron duals produce the 30 and 32 corners, found in the neutron count of elements 25 to 28. Whereas, the 28 neutron count of the 2 previous elements (23 and 24) is found in the Rhombic Dodecahedron. The Rhombic Dodecahedron provides the template for the 4D Hypercube, in the same way that the Rhombic Triacontahedron forms the template for a 6D hypercube. However, what is missing from our geometric understanding is the polyhedra, which represents the 5D hypercube. Whilst this shape has 32 corners, which is the same as the number of corners in the Rhombic Triacontahedron, this polyhedron forms the template of the 6D Cube.
What we propose is that the form that represents the template of the 5D Cube is actually the Dodecahedron. It is a well known fact that a Cube can be nested inside a Dodecahedron, both of which can be contained within the same sized out-sphere. If we give the cube a north/south axis, it can be rotated 4 times in 90° increments. This produces 4 Cubes superimposed over each other. This is not obvious, as each be will appear to be the same from the perspective of 3D space. The second recognised fact is that a Cube can be nested in a Dodecahedron in 5 different orientations. However, what is not recognised is that the Dodecahedron can also be orientated in two different 90° rotations, as the protruding side that sits above each Cube can be positioned vertically or horizontally across the face of each Cube. Again, this occurs at a 90° rotation, which obscures the difference. This produces a total of 40 Cubes, which is the number of cubic Cells needed to form a 5D Hypercube.
Notice the side of the Dodecahedron that appears above the cube, (Yellow line, bottom left), can appear in a horizontal and vertical orientation.
This new explanation of the 5D cube, completes a geometric process that sees the transformation of Cubic space into 4D, the through the Rhombic Dodecahedron, then into 5D with the Dodecahedron, which when compounded with the icosahedron produces the Rhombic Triacontahedron which is the template for the 6D cube. This evolution of dimensional cubic space is aligned with the order of appearance of compound solids in the 1st half of the Extended Jitterbug.
In the final set of solids, we find the Snub Cube and Rhombic Cuboctahedron duels, which defines the radius of the D-orbital Elements. These also produce compounds with mid and in-spheres that, as far as we are aware, currently lack classification. The mid-sphere of the Snub Cube compound exhibits similar pentagonal faces to the Icosidodecahedron, but also includes 6 square faces that a located in the x, y and z axis, where the corners of the Octahedron are found. The out-spheres also exhibit similarities to the Rhombic Tricontahedron. At the centre, the compound of the Cuboctahedron and Rhombic Dodecahedron, which features in many of the atomic geometries discussed. This exhibits a mid-sphere similar to the Rhombic Cuboctahedron, but with two different side lengths that are in proportions of 0.5:√2÷2.
THE
Conclusion
What does this tell us about the atom?
The Atomic is a geometric structure, which can be accurately described by the transformation of the Extended Jitterbug, its duals, and compounds. This model is the first of its kind that unifies the geometric of the atomic nucleus, with that of the electron cloud, and is able to explain the reason for the ferromagnetic and conductive qualities an of different atoms found in the 1st D-orbital set. Unlike present theory, based on the disproven Bohr Model, we find that the uniformity of a wide number of atoms is explained due to the geometric nature of various elements. The theory is also compatible with the Schrödinger Model, and is can be extended into the field of Solid State and Condensed Matter physics. It is the only model that can unify nuclear physics and chemistry, with the physics of lattice structures to form be compounds of these transition elements, which offers simple yet powerful tools for investigating the fundamental nature of our universe.
A Geometric approach to the atom
The fact that this geometric perspective is able to resolve the atomic radii is an important step forwards for atomic theory. Presently, the development of new materials for quantum computing relies on being able to determine the size of a particular atom. By comprehending the nature of geometric principles, we can uncover the inner workings of the atomic fabric.
The implications are far ranging, from the field of lasers, renewable energy generation, and battery storage, to finally being able to understand the reasons for the interactions of biological processes, and even solve the mysteries of life. This article introduces some of the foundational principles of Atomic Geometry, Geoquantum Mechanics, and Geonuclear Physics, which weave together to form the most coherent model of the elements that constitute the whole of existence.
Carry on Learning
This post form part of our net theory of ATOMIC GEOMETRY, GEOQUANTUM MECHANICS, and GEONUCLEAR PHYSICS. Find out more by browsing the post below.


D-Orbital Geometry – Part 2
The 2nd set of D-orbitals contain various anomalies that are explained by the Geometric model of the atom. Part 2 of 3.
2D Orbital Geometry of the Electron Cloud
The 4 types of electron orbital can be mapped to 2D geometry, called the Seed/Flower of Life. This produces a simple geometric pattern that decodes the electron configuration.

S-orbital Geometry
S-orbitals form the only set of elements occupying a spherical shell. Whilst quantum theory suggests it is ‘only applicable’ to these types of atom, investigation of the atomic radius shows a discrepancy of over 100% for some elements.
YOUR QUESTIONS ANSWERED
Got a Question? Then leave a comment below.

Question?
Wow, a fascinating article, but didn’t quite get why the geometries of Iron, Cobalt and Nickel should be ferromagnetic?
ANSWER?
This article is intended as in introduction to the D-orbital geometries of the 1st D-orbital set. More information regarding the ferromagnetic and electrically conductive fields can be found in our post on the geometry of the Brillouin Zones, that examines builds upon the knowledge presented in the article, and covers the subject in greater detail.

Question?
Great article, but you didn’t explain why Element 43 is radioactive?
ANSWER?
Element 43 is found in the 2nd D-orbital set, which is examined in greater detail in our next article on the D-orbital geometries.