The Vesica Piscis, derived from overlaying two circles with equal diameters, has captivated countless cultures throughout history. This enigmatic symbol, with its intersections and geometric proportions, carries deep sacred meaning and has left an indelible mark on various belief systems and scientific theories. Join us as we delve into the rich tapestry of Vesica Piscis, exploring its origins, symbolism, and its profound implications in both the spiritual and scientific realms.
Overview
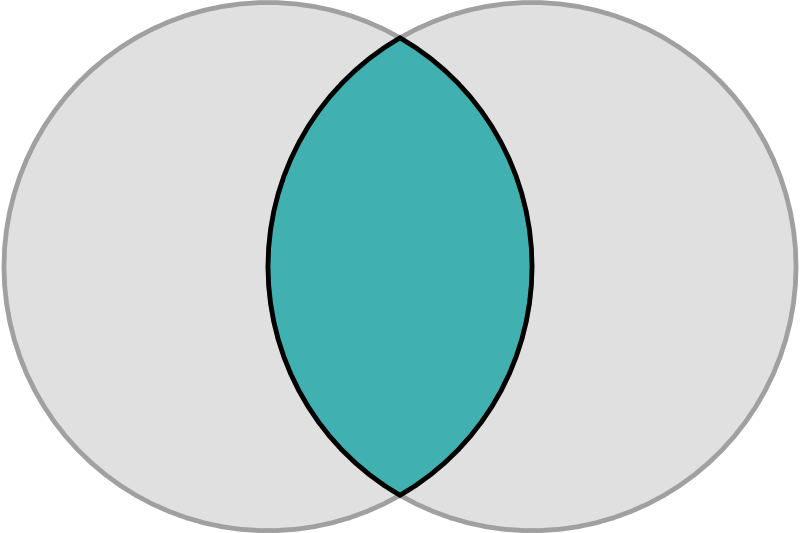
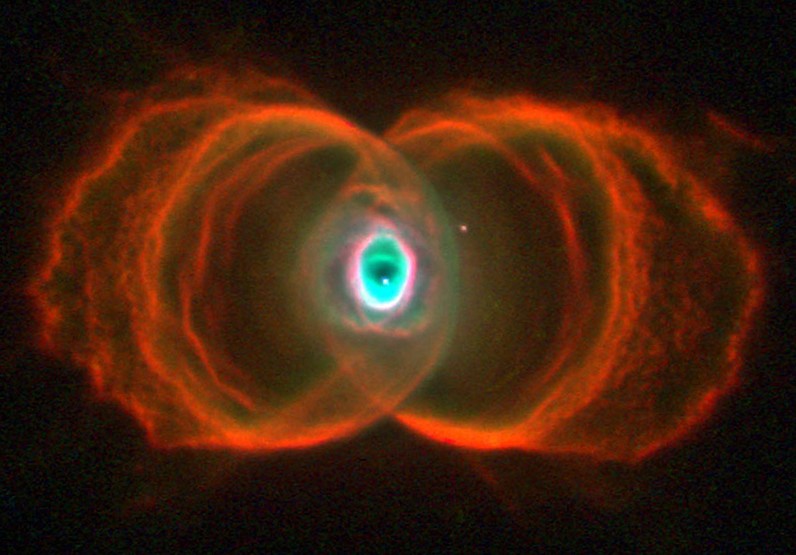
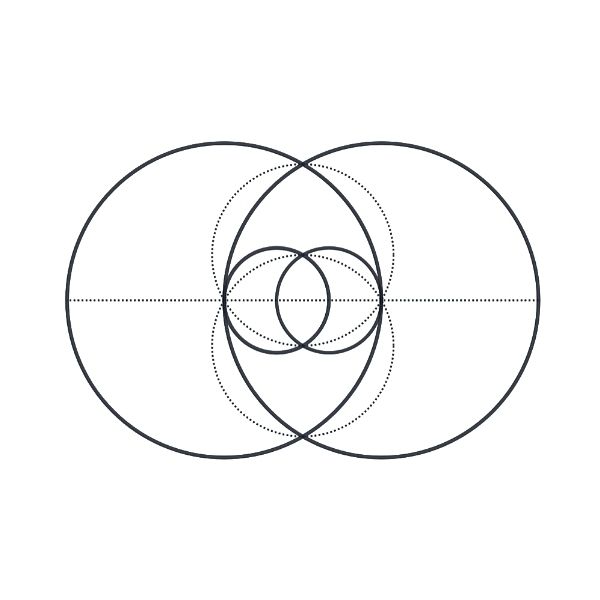
The Vesica Piscis, meaning “fish bladder,” is derived from two circles overlapping in a way that their circumferences touch each other’s centres. The intersectional area is called “mandorla” and resembles an almond. The symbol has origins in Pythagorean history, Christian iconography, and various ancient civilizations. It is associated with the infinite and is used in Venn diagrams. II has implications in Dimensionless Science, and the relationship of the speed of light to the speed of sound. It can be seen to represent the emission of electromagnetic waves to paired electrons, and is found in the shape of deep space nebulae. Overall, the Vesica Piscis shapes the foundations of the universe.
A Sacred Symbol with Diverse Origins
The exact roots of the Vesica Piscis symbol remain elusive. From Pythagorean Greece to Ancient Egypt, Mesopotamia, India, China, and Africa, this symbol has transcended time, manifesting in different cultures across continents. In Ancient Greece, it was revered as the Ichthys, symbolizing the creation of the Syrian Goddess Atargatis. Celtic and Norse cultures associated it with the divine feminine and the vulva of goddesses. In Christian art, notably linked to Mary Magdalene, the Vesica Piscis has been depicted as a representation of the Cosmic Mother.
Universal Symbolism of Infinity
The circle, universally recognized as a symbol of the infinite and perfection, finds its expression in Vesica Piscis. With no vertex, no beginning, and no end, the circle embodies limitless potential and divine essence. The Vesica Piscis, formed by two intersecting circles, takes this symbolism further with its sacred geometry, portraying unity, creation, and the convergence of celestial forces.
Exploring its Geometric Proportions
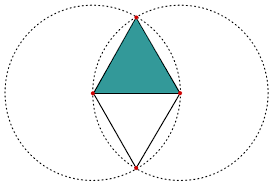
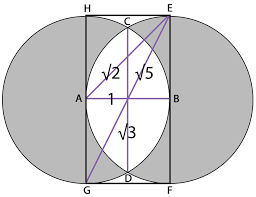
The geometric aspects of the Vesica Piscis hold both beauty and profound mathematical implications. Two contiguous equilateral triangles can be inscribed within the Vesica Piscis, revealing the relationship between vertical and horizontal proportions as 1:√3. We also find √2 and √5, are encoded into its structure, which are the genesis for the creation of the Silver and Golden ratios.
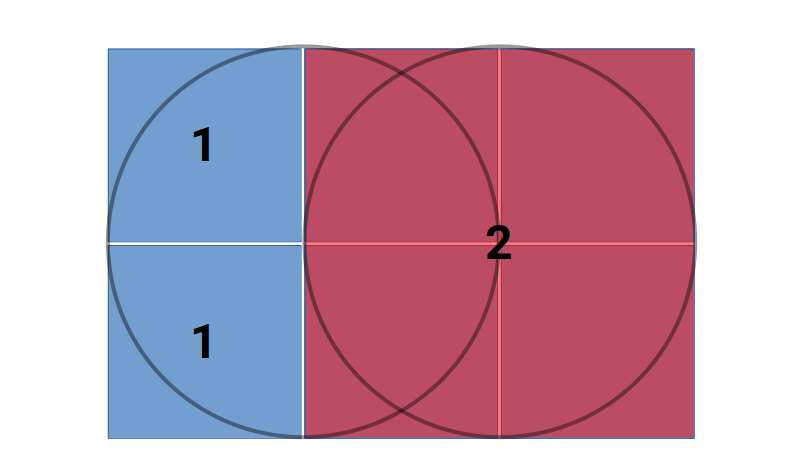
This fascinating ratio finds its way into numerous architectural marvels and even permeates Venn diagrams, challenging the traditional notion that 1+1 equals only 2.
Scientific Significance
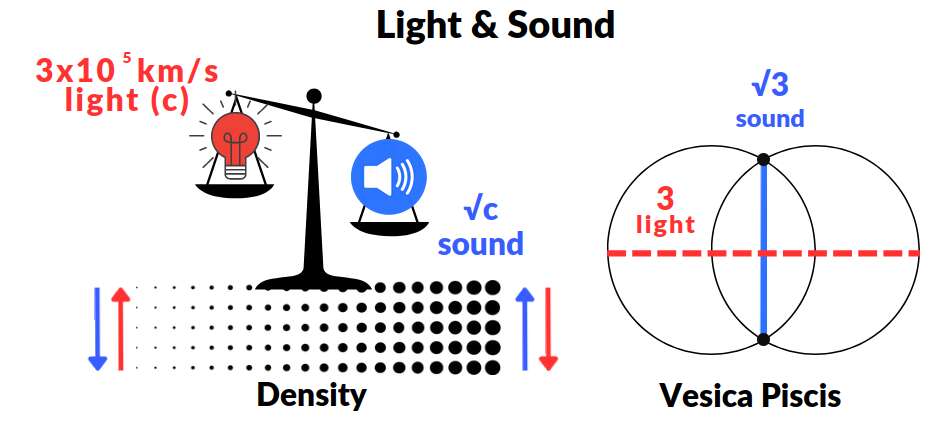
Beyond its spiritual connotations, the Vesica Piscis also plays a significant role in scientific realms. The Geometric Universe Theory, which employs dimensionless science, correlates the dimension of the Vesica Piscis through the horizontal with the speed of light set to 3. This dimension is intricately linked to the maximum speed of sound found in an infinitely dense medium, as observed in baryonic acoustic oscillations (BAOs) within the cosmic microwave background.
Vesica Piscis and the Fibonacci spiral
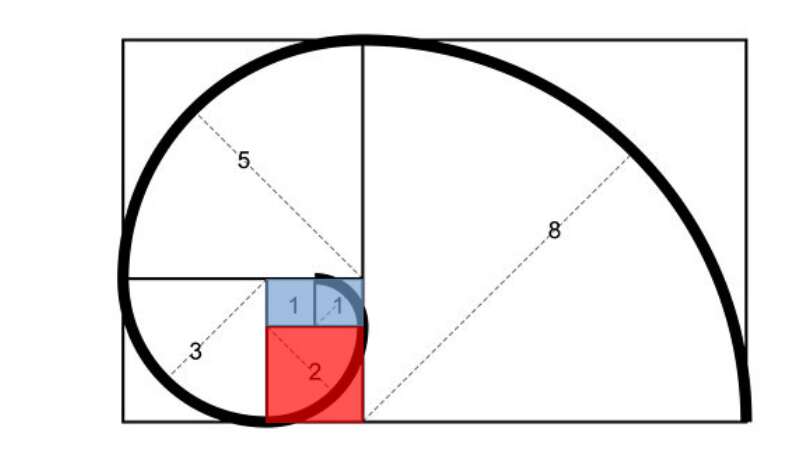
The Vesica Piscis fits perfectly within a 2 by 3 rectangle. This also initiates the Fibonacci spiral, which is observed in a wides range of natural phenomena. From flower formations to fruit, to the proportions of a wide range of lifeforms, and even galactic spiral, the Fibonacci appear to structure the domain of matter.
From the Microcosmic to the Macrocosmic
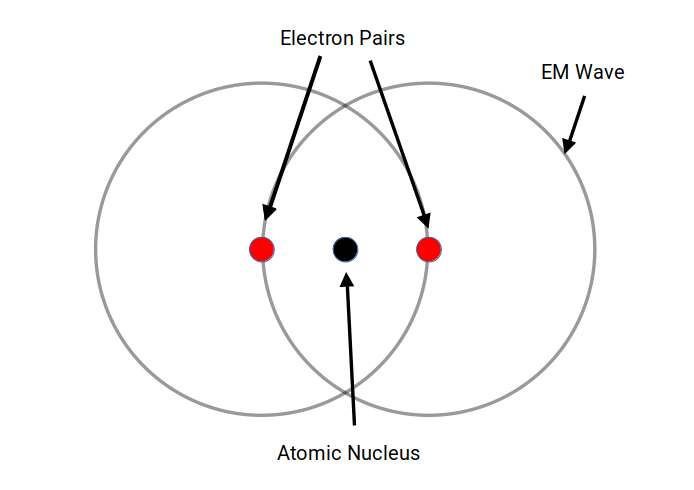
The Vesica Piscis’ influence spans from the microcosmic realm to deep space. Electrons, forming pairs with up and down spins, release electromagnetic waves when transitioning to lower energy states, which can be represented by the Vesica Piscis. This symmetrical pattern also manifests in the awe-inspiring appearance of deep space nebulae. Thus, from the foundational building blocks of atoms to the expanse of the universe, the Vesica Piscis continually shapes and influences our cosmic existence.
THE
Conclusion
The Vesica Piscis stands as a powerful and timeless symbol that has transcended cultural and religious boundaries throughout history. From its mysterious origin to its representation in art, science, and the cosmic realm, this symbol continues to captivate our collective imagination. As we delve into the interconnectedness of the universe, the enduring presence of the Vesica Piscis serves as a reminder of the underlying unity and profound mysteries awaiting our exploration.
Carry on Learning
Discover more about SACRED GEOMETRY

Taoism Symbol
Taoism Philosophy Taoism, also known as Daoism, is a Chinese philosophy or religious tradition that is attributed to Laozi or Lao Tzu (c. 500 BCE). It emphasises living in harmony with the Tao, which is a Chinese word for path, way, or principle. Its central teaching is based on the
Symbol
Sacred Geometry Symbols These are all the spiritual and religious symbols from Islam, Christianity, Judaism to Buddhism, Hinduism, Jainism and Taoism. Most symbols are being shared between the different religions, yet most are known to be related to a specific religion.
Hinduism Symbol
Hindu Symbolism Primarily spread in India, the roots of Hinduism are found in the oldest scriptures of the world, the Vedas. Core beliefs are the goals of life, which are morals, prosperity, passion, and libration. Many Hindu symbols are imbued with spiritual meaning, which also overlap with Buddhism and Jainism.