Geo-Quantum Mechanics (GQM) is an extension to the field of Atomic Geometry. Whilst Atomic Geometry focuses on the S, P, D, and F orbitals, produced from the Hydrogen atom, GQM examines the nature of the electron cloud for the entire periodic table. It presents a more advanced geometric model of the atom that takes into account the addition of neutrons and protons in the nucleus of each element.
The result is the worlds most accurate atomic model in terms of atomic radii, that supersedes the Bohr Radius and the Van-Da-Waal Radius by over 100% in some cases.
Overview
Geo-Quantum Mechanics explores the electron configuration, and size of the atomic radii in relation to the structure of Platonic and Archimedean Solids outline in our concept of Atomic Geometry.
At first appearance, the radii of the atoms distributed throughout the stable element appears to be random and unpredictable, failing our current theoretical models. Yet through the lens of geometry, a pattern begins to emerge that can explain many of the deep mysteries of traditional quantum physics
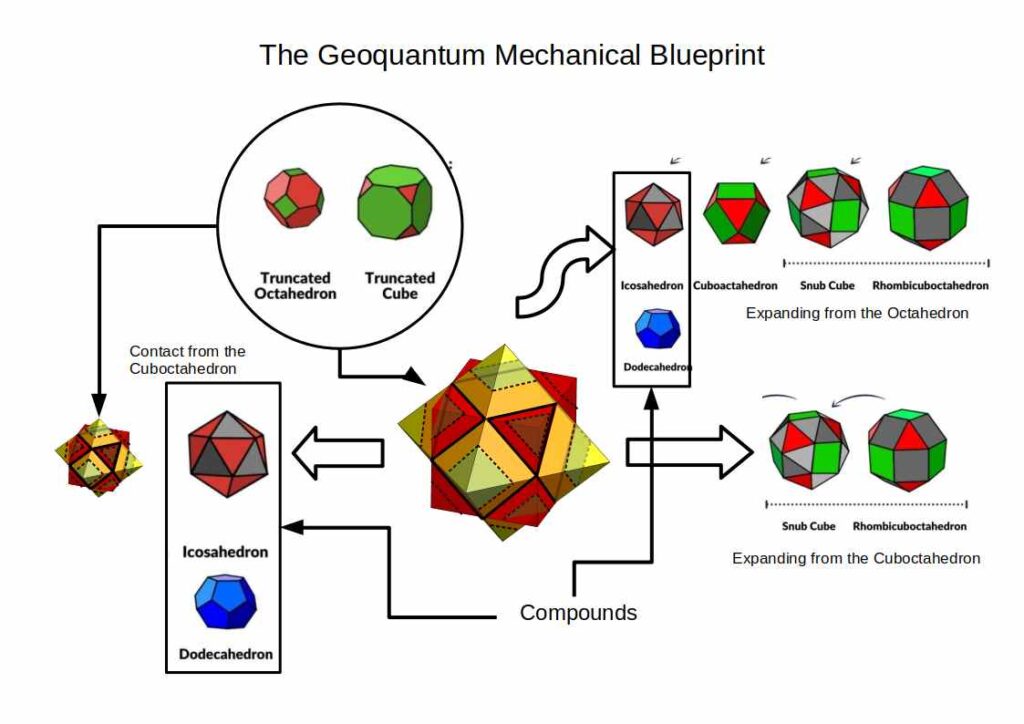
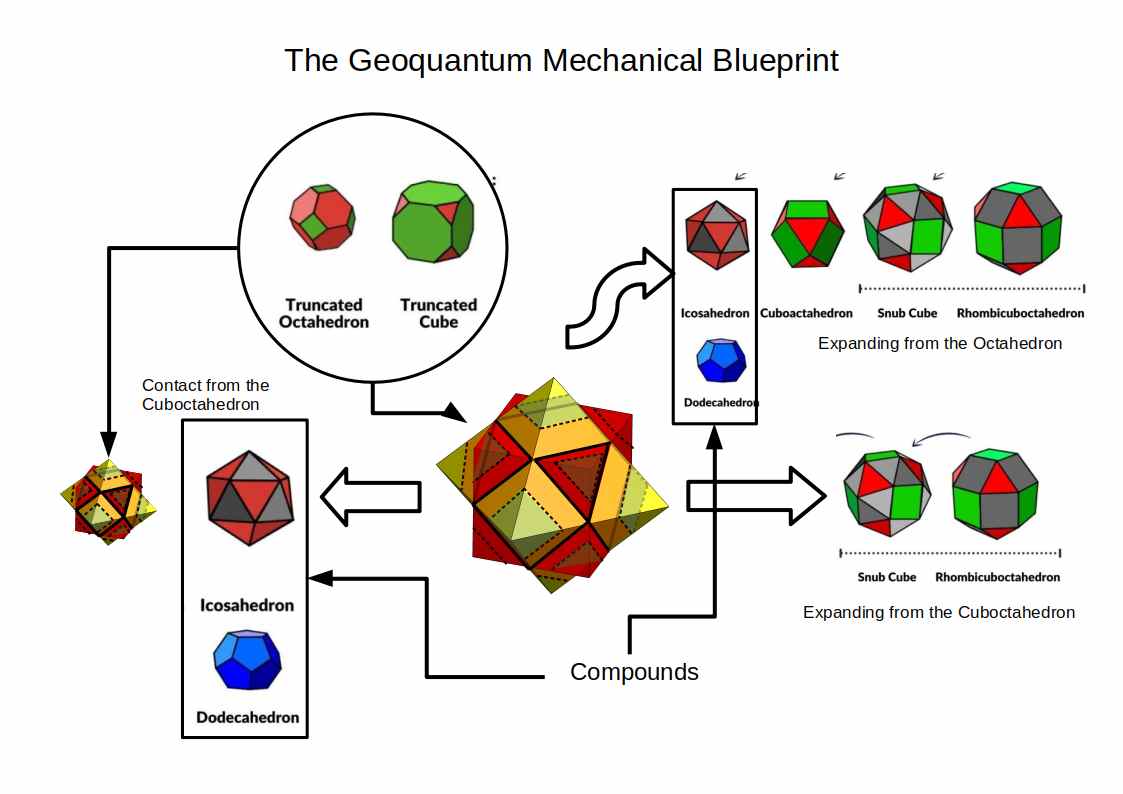
The image above outlines the geo-mechanical blueprint, which is used to produce an accurate model of the atomic radii for all stable elements on the periodic table. When the results are compared to the standard model, which uses the Bohr and Van da Waal radius, we find the Geo-Quantum Mechanics provides a far more accurate description.
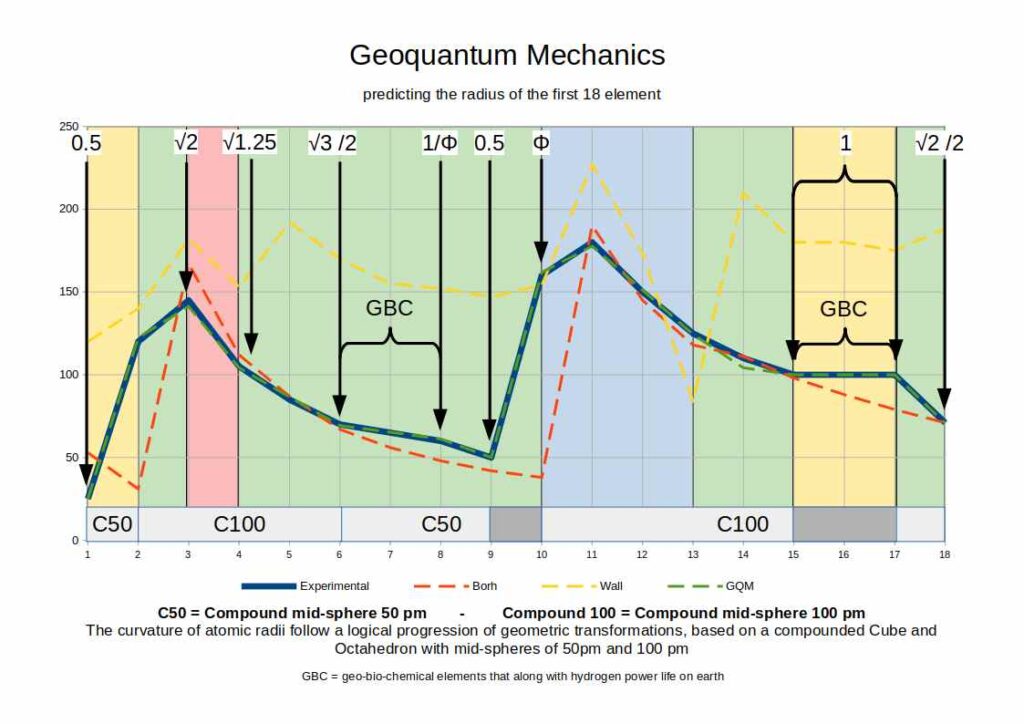
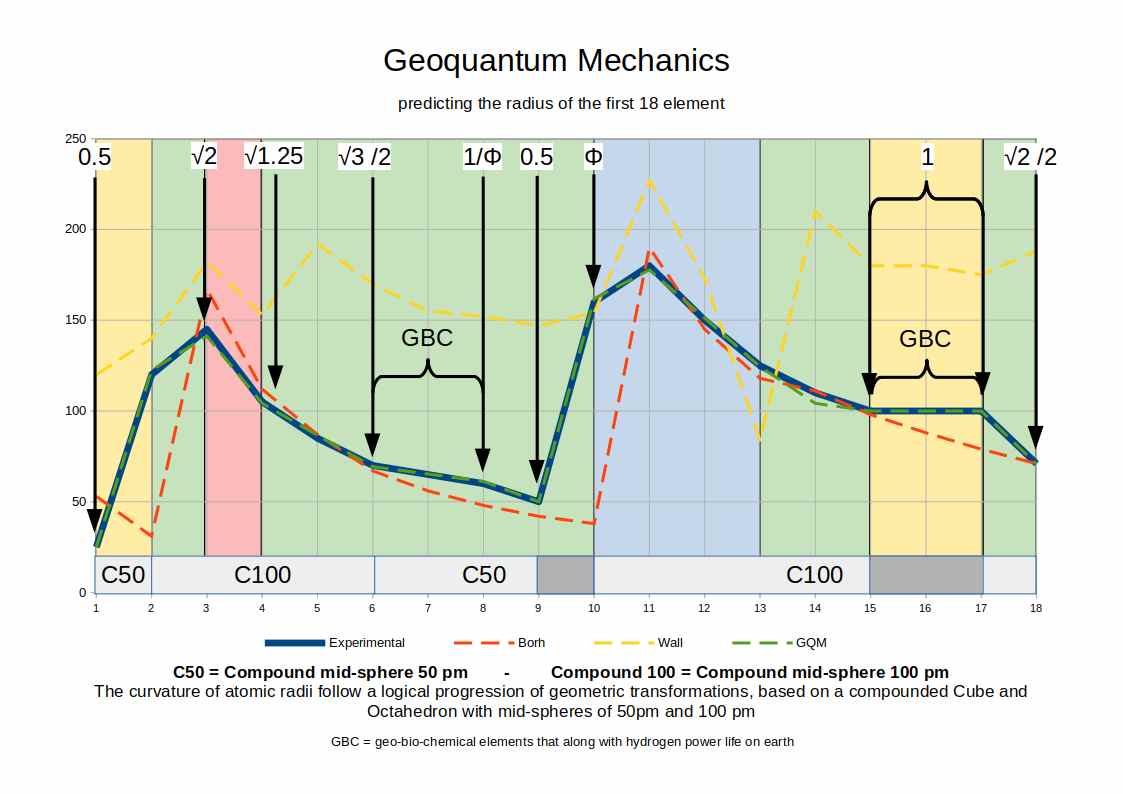
Above, we see the radii for the first 18 elements on the periodic table. The solid blue line represents the results of experimental measurements. The dotted green line that in appears to superimpose the blue line is the model generated by the Geo-Quantum model. Except for element 14 (where there is a small discrepancy, the rest of the elements appear as an almost perfect match. Compared to the Red and yellow line that are the predictions made by our present scientific models, we can see that Geo-quantum Mechanics offers a far more accurate description.
Key Points
-
Geoquantum Mechanics is the worlds most accurate modle of the atom in terms of atomic radii
-
It is based on a simple to understand geometric template
-
It offer new explainations for many phenomina found in the quantum world
THE
Concept
Geometric mapping the Atomic Radii
The cube of space
Physical phenomena is measured within the Cubic nature of space. The Cube is the only Regular Space-filling Platonic Solid, which provides an X, Y and Z axis. This allows us to qualify distance measurements in terms of length, breadth, and depth.
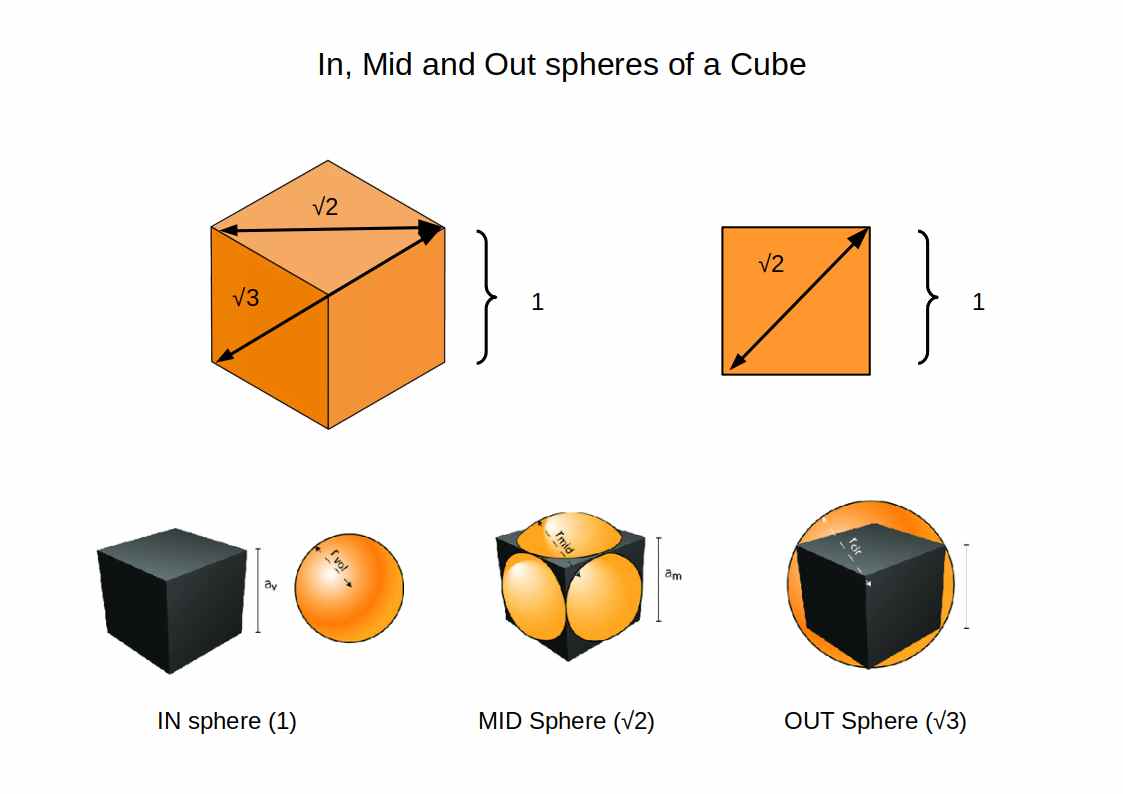
All solids exhibit an In-sphere, Mid-sphere, and Out-sphere, (or circumsphere). We prefer to use the words IN, OUT and MID to maintain clarity. Let us take the example of a Cube with a side length of 1. The diagonal of its side length will measure √2, and the distance between opposite corners will be √3. therefore, a sphere placed inside of the cube will have a diameter of 1, the IN-sphere. By increasing the size of the sphere, it will touch the centre of each side, producing a MID-sphere of √2. Finally the OUT sphere encompasses the Cube.
The cube of space
In the concept of Atomic Geometry, we show that electron can fill specific places within a cube.
We can compare this concept to the average size of each atomic orbital and find that almost every block exhibits points structure where a sequential series of elements share exactly the same radii.
Putting aside the P1 and P3 orbitals for a moment and turning attention to the other orbitals, we notice there seems to be a specific radius where each set levels off. P2 elements level off at around 100 pm, whereas P4, all the D-block elements, level off at around 1.4Å. The first half of the F-block elements have radii of about 1.85Å, falling to 1.75Å at around the halfway point.
If we imagine a cube with a side length of 2Å then we find that each type of orbital radii roughly falls over the point where the IN, MID and OUT sphere are located. Whilst this is just a rough overview, it is a good starting point for scaling our atomic model the values of the radii. Not only do the orbitals fall at around the correct radius, that also fall into the cube in the exact configuration we have allocated for each orbital type.
These values are only a rough guide, and in reality there is a tremendous variation in size for each type of atom. However, by using the principles that transform Platonic into Archimedean Solids, we are able to generate a far more accurate match. So accurate, in fact, that it supersedes all other existing predictions.
Geometric Functions
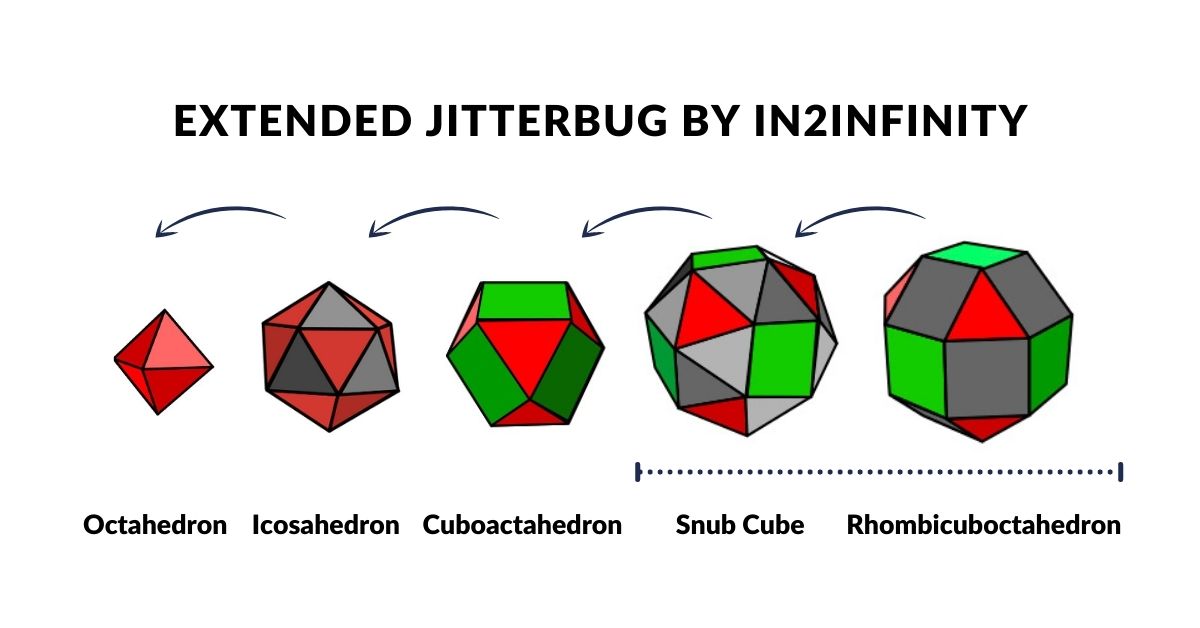
We are not the first people to suggest that the atom follow a geometric structure. A similar idea of the atom was conceived of by Buckminster Fuller. He discovered that by collapsing the square faces of a Cuboctahedron into two triangles will create an Icosahedron. Continuing this process produces an Octahedron at the final stage. This transformation was termed the ‘Jitterbug’ and was suggested by Fuller to be in operation within the atomic structure. Both the Octahedron and Cuboctahedron are 2 forms we have identified from the orbital geometries.
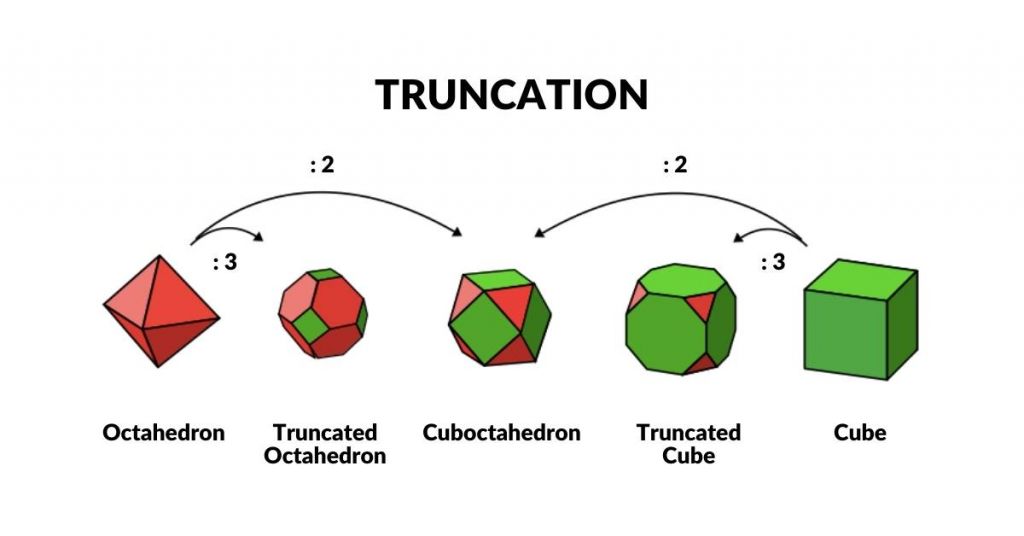
Truncation
The second important geometric transformation used in Geo-Quantum mechanics is ‘Truncation’. This is enacted by the division of the side length of a Platonic Solid into two or three. By dividing the side of a Cube or Octahedron in half, the Cuboctahedron is formed. By dividing the sides into three, the corners of each polyhedron can be removed, forming the truncated Cube or Octahedron.
We can place these objects in a row, with the Octahedron at one end and the Cube at the other. Comparing this to the ‘Extended Jitterbug’ both begin with an Octahedron (P-orbital). The truncated series collapses the Octahedron into a Cuboctahedron, whereas the Jitterbug expands into the Cuboctahedron. The first diminishes in size and the latter grows in size, meaning that the two Cub-octahedra exhibit side lengths that are double in size.
Geo-Quantum Blueprint
We can combine the three previous geometric concepts, the Jitterbug, Truncation, and Compounds, to produce the ‘Geoquantum Blueprint’ that we can use to map the atomic structure.
The compound of the Cube and Octahedron, share the same mid-sphere, which each defines a Cuboctahedron at its centre. Both the Octahedron and Cube can have a portion of their corners removed to produce their truncated versions.
The Octahedron can explode through the Jitterbug process, to create a larger Icosahedron and Cuboctahedron (double in size), and then on to create the Snub Cube and Rhombic-Cuboctahedron.
The Cuboctahedron in the centre of the cube/octahedron compound can also expand and shrink through the same jitterbug process. As the Cuboctahedron collapses into a smaller octahedron, so new compounds can be formed, firstly from the Icosahedron/dodecahedron pair and then another Octahedron/Cube. This can also be truncated, and also contains a smaller Cuboctahedron as its centre. Again, it can expand and contact in size, through the extended jitterbug process.
Each of these polyhedra has an IN, MID, and OUT sphere, most of which exhibit different sizes. However, some of these spheres do fall in exactly the same space. The mid-sphere of the Cube/Octahedron compound, which also form the out-sphere of the Cuboctahedron, for example.
This Geo-mechanical scaling is what we believe structures, the not just the radii of the atomic shells, but more incredibly, the variation of atomic radii for every element on the periodic table.
Predicting Atomic Radii
When we think of an atom, we often imagine that the size must be increasing in incremental steps as more electrons begin to fill each shell. However, this is far from the truth. The atomic radius seems to vary widely for each type of atom. Additionally, the different sizes seem not to follow any kind of predictable pattern. Sometimes we see noble gases like Helium (2) and Neon (10) expand in size, whereas others, such as Argon (18), seem to contract in size. At the same time, we find certain element exhibiting the exact same radius. Why?
Using the Geoquantum Mechanical model, we are able to explain this large variation, whilst maintaining a logical geometrical process. In this way, we can produce a curvature that almost exactly matches the experimentally measured values for all the atomic radii on the periodic table.
Currently, there are two sets of data that are used to try and calculate the atomic radii. The first is the Bohr Radius, which is a theoretical value based on an infinitely dense atomic nucleus. The second is the Van da Waal radius, which considers the atom as a hard shelled sphere.
However, for the majority of elements we see that the predicted values do not even come close to the data extrapolated by experimental results, that are accurate within a tolerance of about 5 picometres.
The table below shows the results generated for each atomic radii for the first 18 elements. The blue line provides the results generated by experimental data. The dotted green line might be hard to see, as it is so close to the measured data, whereas the red dotted line depicted the data derived from the Bohr radius, and the Yellow line from the Van da Waal radius. Clearly, Geoquantum mechanics is a more accurate representation of experimental results
All of these radii are derived from the Geoquantum Blueprint. Two Cube/Octahedron Compounds are scaled through the extended jitterbug, so that the first exhibits a mid-sphere radius of 50pm and the second a radius of 100pm
In the graph above the green sections produce radii based on the Cube, Truncated Cube, Snub Cube, or Rhombic-Cuboctahedron, the red section is based solely on the Octahedron, and the blue section is based on the Icosahedron/dodecahedron compound.
The implication it that the space around the atom is geometric, and that is why the electrons are held in such stable ‘orbits’. This insight sheds a completely new light on the functioning of the atom, which validates the theory of Atomic Geometry, and introduces another new field of science to the world. Geo-Quantum Mechanics.
Data Sheet
THE
Conclusion
What does this tell us about the Atom?
The suggestion of Geo-Quantum mechanics is the is it the space surrounding the Nucleaus, that quantises the electron cloud, that accounts for the quantisation of each shell at a specific energy level.
Geo-Quantum Mechanics: The most accurate model of the atom to date.
Current atomic theory is unable to account for the difference in size between the first two atoms on the periodic table. Geo-quantum Mechanics can define the whole set of stable element to an almost exact degree, which for most cases, is in within the range that accounts for experimental error.
Carry On Learning
This article is part of our new theory, Atomic Geometry
browse more interesting post from the list below
2D Orbital Geometry of the Electron Cloud
The 4 types of electron orbital can be mapped to 2D geometry, called the Seed/Flower of Life. This produces a simple geometric pattern that decodes the electron configuration.
D-Orbital Geometry – Part 3
The 3rd set of D-orbitals are the last to form stable elements. The geometric explanation revels a 6D structure which terminates at the end of the Metatron’s Cube.
D-orbital Geometry – Part 1
D-orbitals form cross shapes lobes that unify on the x, y, and z axis to produce a hypercubic model of the electron cloud
YOUR QUESTIONS ANSWERED
Got a Question? Then leave a comment below.
Question?
I thought quantum theory was accurate of billionths of a degree of accuracy?
ANSWER?
This might be true for the hydrogen atom (1), however, it is not the case for the other elements. Often, traditional QM looks inside the atom to discover information about subatomic particles. The Muon is one example where QM fails in its predictions. If we begin to examine atoms that contain Neutron (all atoms above hydrogen) we see the QM struggles to maintain its predictions.
Question?
Is this model of the atom applicable to all the elements on the periodic table?
ANSWER?
There are 81 stable elements on the periodic table. We have found that all can be mapped by the Quantum Geo-Mechanical Model.
STILL Looking for Answers?
Ask a question…
