Welcome, to this online guide to Euclidean Geometry, produced by In2infinity, and written by Sunil JAnkar. In this section, we will explore the concept of Similarity.
What is a Similarity?
The idea of similarity is an important one in geometry. Similar figures are figures that are the exact same shape, but are different sizes. In different words, two figures are similar if one figure can be obtained from the other by uniformly scaling (enlarging or reducing), possibly with additional translation, rotation and reflection.
For example, all circles are similar to each other, all squares are similar to each other, and all equilateral triangles are similar to each other. On the other hand, ellipses are not all similar to each other, rectangles are not all similar to each other, and isosceles triangles are not all similar to each other.

Most mathematicians consider congruent shapes to also be similar (going beyond similarity to be identical in size). Yet it must be kept in mind that, though congruent shapes are automatically similar, similar shapes are not automatically congruent. The most common way to use similar figures is knowing the size of a small figure can help you estimate the size of a larger, unknown measurement. Similar triangles provide the basis for many proofs in Euclidean geometry. We will discuss similar polygons in later sections but before we move on to that we need to understand another key concept in mathematics, the idea of ratio and proportion.
Proportion
Proportion is the expression of equality between two equal ratios. Where ratio is defined as the comparison or simplified form of two quantities of the same kind. This relation indicates how many times one quantity is equal to the other; or in other words, ratio is a number which expresses one quantity as a fraction of the other. A ratio is an indication of the relative size of two magnitudes.
Symbols
Proportion is written in one of the following forms:
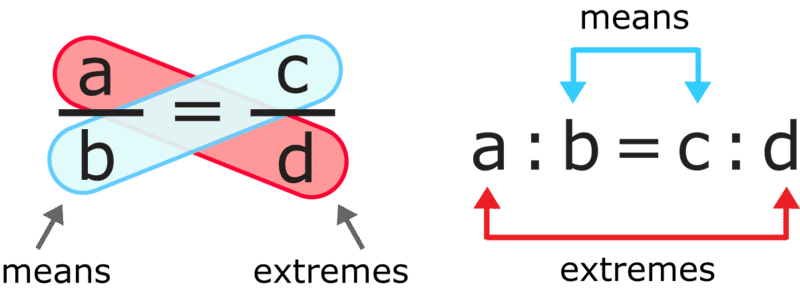
a : b = c : d
a : b :: c : d
a/b = c/d
It is read as, “a is to b as c is to d” or “the ratio of a to b is equal to the ratio of c to d.”
Terms
In a proportion, the four quantities compared are called the terms. In the example of a:b = c:d, the first and fourth terms are called the extremes; a and d. The second and third terms, the means. b and c.
Also, a and c are the antecedents (top pair), whereas b and d are the consequents (bottom pair).
Fourth Proportion:
The fourth term of a proportion is called the fourth, which is proportional to the terms taken in order. Thus, in the proportion a:b = c: d, d is the fourth proportional to a, b, and c.
Continued Proportion:
The quantities a, b, c, d, and e are said to be in continued proportion, if a : b = b : c = c : d =.d : e.
If three quantities are in continued proportion, the second is called the mean proportional between the other two, and the third is called the third proportional to the other two.
For example, in the proportion a:b = b:c, b is the mean proportional between a and c, and c is the third proportional to a and b.
Proportion Theorems
The nature of proportion gives rise to a number of key theorems in geometry.
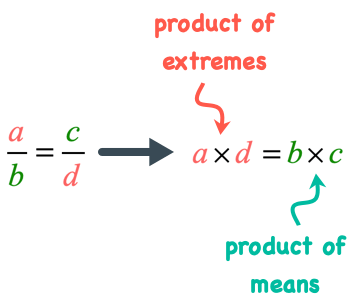
1. In any proportion the product of the extremes is equal to the product of the means.
Corollary:
- The mean proportional between two quantities is equal to the square root of their product.
- If the two antecedents of a proportion are equal, the two consequents are equal.
- If the product of two quantities is equal to the product of two others, either two may be made the extremes of a proportion in which the other two are made the means.
2. If four quantities are in proportion, they are in proportion by alternation; that is, the first term is to the third as the second term is to the fourth.
3. If four quantities are in proportion, they are in proportion by inversion; that is, the second term is to the first as the fourth term is to the third.

4. If four quantities are in proportion, they are in proportion by composition; that is, the sum of the first two terms is to the second term as the sum of the last two terms is to the fourth term.
5. If four quantities are in proportion, they are in proportion by division; that is, the difference of the first two terms is to the second term as the difference of the last two terms is to the fourth term.
6. In a series of equal ratios, the sum of the antecedents is to the sum of the consequents as any antecedent is to its consequent.
7. Like powers of the terms of a proportion are in proportion.
8. If three quantities are in continued proportion, the first is to the third as the square of the first is to the square of the second.
Nature of the Quantities in a Proportion
Although we may have ratios of lines, or of areas, or of solids, or of angles, we treat all of the terms of a proportion as numbers.
1. If a line is drawn through two sides of a triangle parallel to the third side, it divides the two sides proportionally.
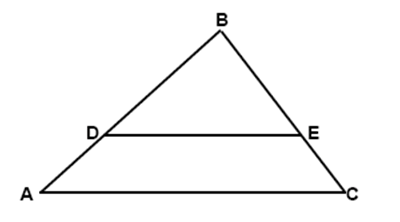
Corollary:
1. One side of a triangle is to either of its segments cut off by a line parallel to the base, as the third side is to its corresponding segment.
2. Three or more parallel lines cut off proportional intercepts on any two transversals.
2. If a line divides two sides of a triangle proportionally from the vertex, it is parallel to the third side.
Dividing a Line into Segments
If a given line AB is divided at O, a point between the extremities A and B, it is said to be divided internally into the segments AO and OB. If it is divided at O, along a point in the prolongation of AB, it is said to be divided externally into the segments AO and OB.
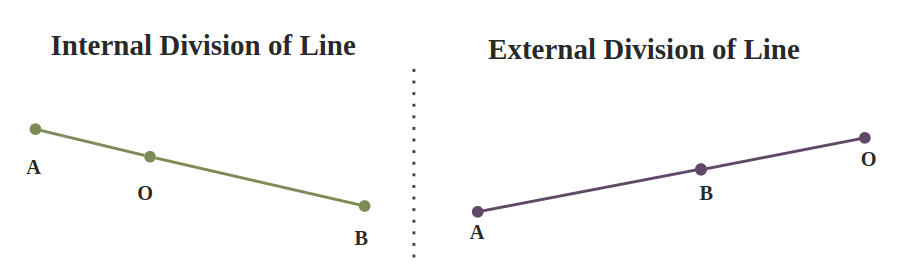
Harmonic Division
If a given straight line is divided internally and externally into segments having the same ratio, the line is said to be divided harmonically.
Theorems
1. The bisector of an angle of a triangle divides the opposite side into segments which are proportional to the adjacent sides.
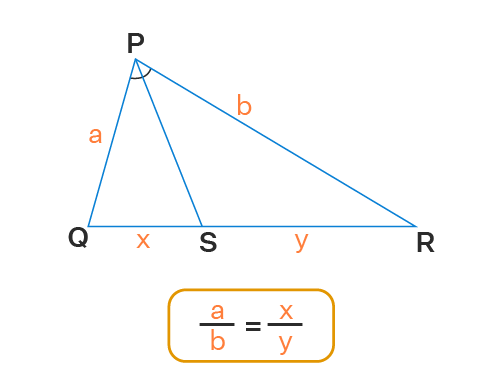
2. The bisector of an exterior angle of a triangle divides the opposite side externally into segments which are proportional to the adjacent sides.
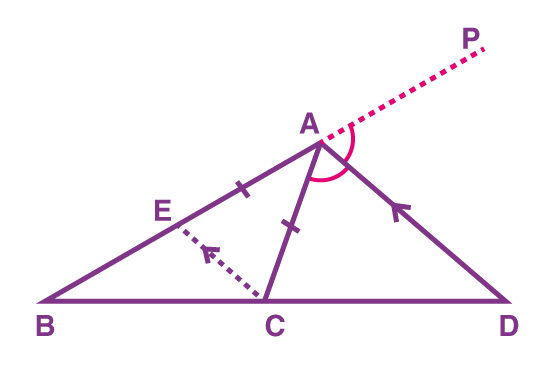
Corollary: The bisectors of the interior angle and the exterior angle at the same vertex of a triangle, meeting the opposite side, divide that side harmonically.
SIMILAR POLYGONS
Polygons that have their corresponding angles equal, and their corresponding sides proportional, are called similar polygons.
Corresponding Lines
In similar polygons, those lines or sides that are similarly situated with respect to the equal angles are called corresponding lines. Corresponding lines are also called homologous lines.
Ratio of Similitude
The ratio of any two corresponding lines in similar polygons is called the ratio of similitude of the polygons. The primary idea of similarity is likeness of form. The two conditions necessary for similarity are:
- For every angle in one of the figures, there must be an equal angle in the other.
- The corresponding sides must be proportional.

SIMILAR POLYGON THEOREMS
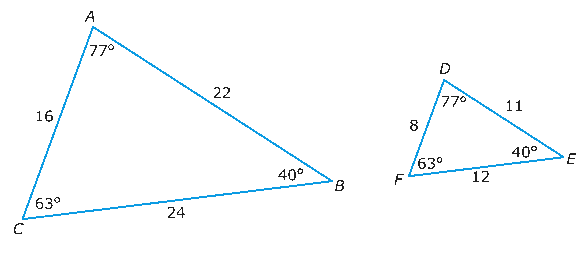
Two mutually equiangular triangles are similar.
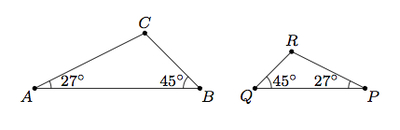
Corollary – Triangles
- Two triangles are similar if two angles of the one are equal respectively to two angles of the other.
- Two right triangles are similar if an acute angle of the one is equal to an acute angle of the others
- If two triangles have an angle of the one equal to an angle of the other, and the including sides proportional, they are similar.
- If two triangles have their sides respectively proportional they are similar.
- Two triangles which have their sides respectively parallel, or respectively perpendicular, are similar.
Corollary – Polygons
- The perimeters of two similar polygons have the same ratio as any two corresponding sides.
- If two polygons are similar, they can be separated into the same number of triangles, similar each to each, and similarly placed.
- If two polygons are composed of the same number of triangles, similar each to each, and similarly placed, the polygons are similar.
Corollary – Right Trinagles
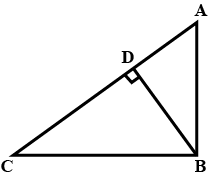
- If in a right triangle, a perpendicular is drawn from the vertex of the right angle to the hypotenuse:
- The triangles thus formed are similar to the given triangle, and are similar to each other.
- The perpendicular is the mean proportional between the segments of the hypotenuse.
- Each of the other sides is the mean proportional between the hypotenuse and the segment of the hypotenuse adjacent to that side.
- The squares on the two sides of a right triangle are proportional to the segments of the hypotenuse adjacent to those sides.
- The square on the hypotenuse and the square on either side of a right triangle are proportional to the hypotenuse and the segment of the hypotenuse adjacent to that side.
Corollary – Circles
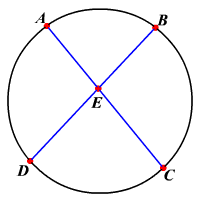
- The perpendicular from any point on a circle to a diameter is the mean proportional between the segments of the diameter.
- If a perpendicular is drawn from any point on a circle to a diameter, the chord from that point to either extremity of the diameter is the mean proportional between the diameter and the segment adjacent to that chord.
- If two chords intersect within a circle, the product of the segments of the one is equal to the product of the segments of the other.
Secant to a Circle
A secant from an external point to a circle is understood to mean the segment of the secant that lies between the given external point and the second point of intersection of the secant and circle,
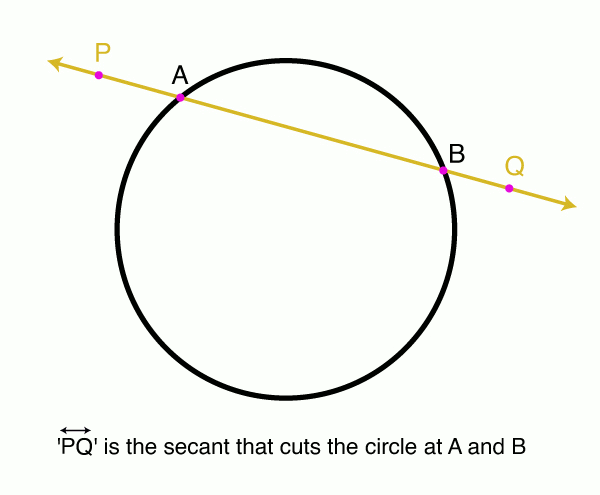
If from a point outside a circle a secant and a tangent are drawn, the tangent is the mean proportional between the secant and its external segment.
Corollary:
- If from a fixed point outside a circle a secant is drawn, the product of the secant and its external segment is constant in whatever direction the secant is drawn.
- The square on the bisector of an angle of a triangle is equal to the product of the sides of this angle diminished by the product of the segments made by the bisector upon the third side of the triangle.
- In any triangle, the product of two sides is equal to the product of the diameter of the circumscribed circle by the altitude upon the third side.
The Golden Ratio
If a line is divided into two segments such that one segment is the mean proportional between the whole line and the other segment, the line is said to be divided in extreme and mean ratio. The division of a line in extreme and mean ratio is often called the Golden Section, golden ratio, golden mean.
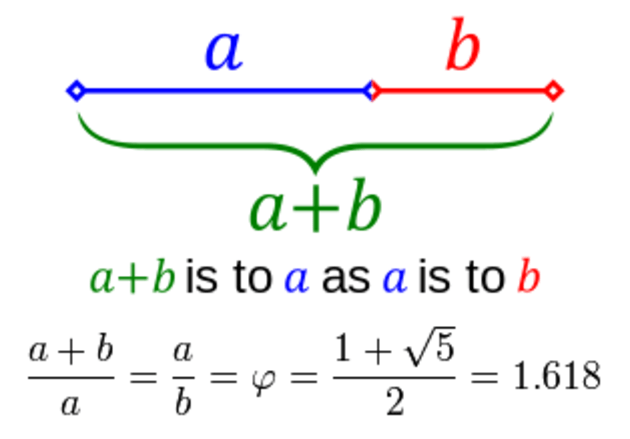
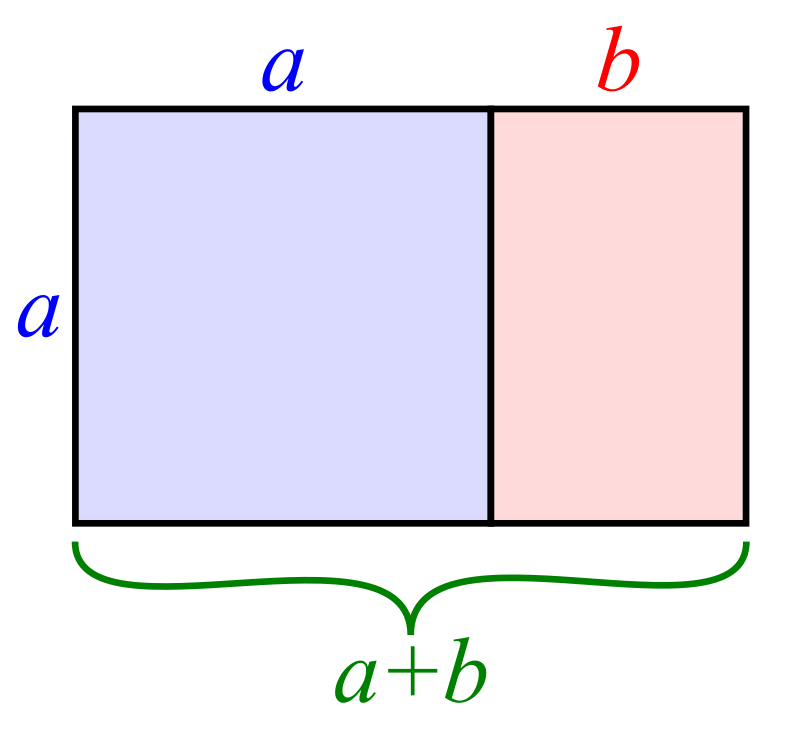
Golden Rectangle
The golden ratio is a numerical celebrity among maths enthusiasts. It is the ratio of side lengths on a very special rectangle. If we take this rectangle and cut the largest square possible off of it, we are left with another rectangle with exactly the same side length ratios as the first one. This construction defines a unique relationship between the lengths of the sides, and any rectangle whose sides have that relationship is called a golden rectangle. If the shorter side of a golden rectangle has length 1, the longer side has length (1+√5)/2, or about 1.618.
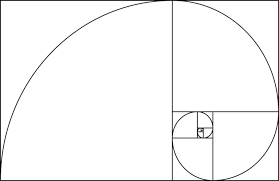
Golden spiral
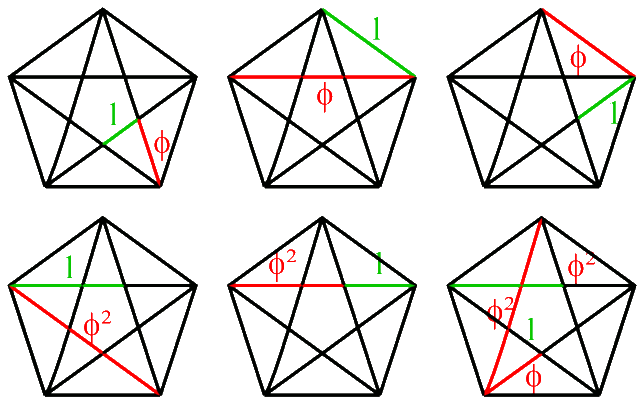
Golden Ratio and the pentagon
The golden ratio appears as the diagonal of a regular pentagon. The ratio between the diagonal of a regular pentagon to its side is golden ratio.
Construction of the Golden Mean
PROBLEM
To divide a given line in extreme and mean ratio. Given the line AB. Required to divide AB in extreme and mean ratio.
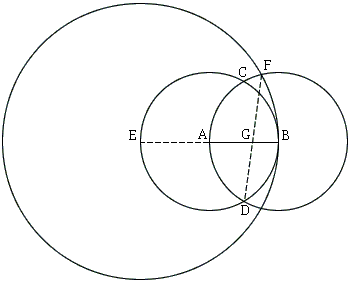
Construction Steps:
- For a given segment AB of length 1, form circles A(B) and B(A).
- Let C and D be the intersections of A(B) and B(A).
- Extend AB beyond A to the intersection E with A(B).
- Draw E(B) and let F be the intersection of E(B) and B(A) farther from D.
- DF intersects AB in G. AG:BG=φ.
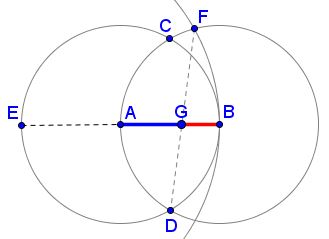
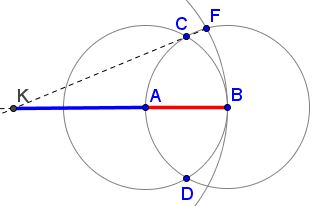
In this example, phi is determined through internal division of the initial line AB. It can also be found externally, by extending the line EAB and CF to form a new point K. Now AB = 1 and KA=1.618, phi. Added together the result is 2,618… or Φ².
The Silver Ratio
There are other similarly constructed irrational numbers that are a little less well-known than the celebrated golden cousin. A lesser known such ratio is the silver ratio or silver mean. In mathematics, two quantities are in the silver ratio (or silver mean) if the ratio of the smaller of those two quantities to the larger quantity is the same as the ratio of the larger quantity to the sum of the smaller quantity and twice the larger quantity
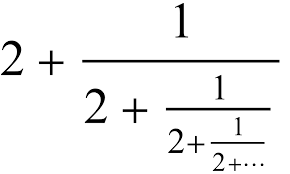
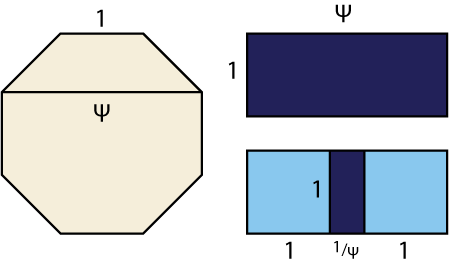
Silver Rectangle
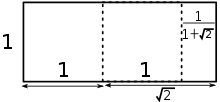
For a rectangle with the silver ratio, we have to cut off two squares and be left with one rectangle that has the same aspect ratio as the first one.
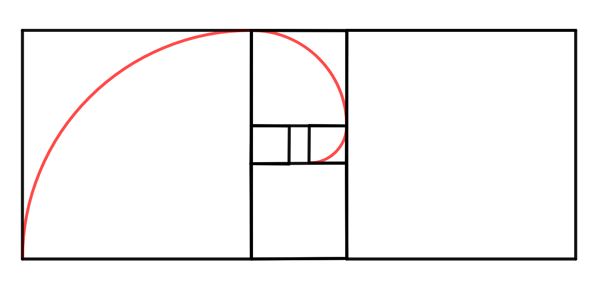
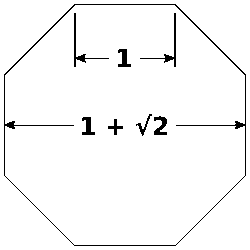
Silver Ratio and the octagon
As the golden ratio is connected to the regular pentagon (first diagonal/side), the silver ratio exists as connected to the regular octagon (second diagonal/side).
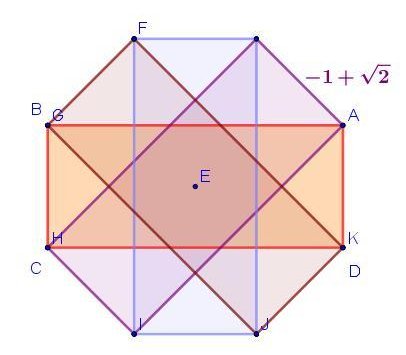
Construction of the Sliver Mean
PROBLEM 1
To find a third proportional to two given straight lines.
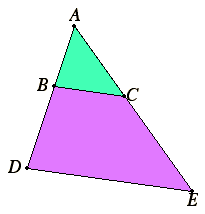
Let AB and AC be the two given straight lines, and let them be placed so as to contain any angle. It is required to find a third proportional to AB and AC. Produce them to the points D and E, and make BD equal to AC. Join BC, and draw DE through D parallel to it. Then since BC is parallel to a side DE of the triangle ADE, therefore, proportionally, AB is to BD as AC is to CE. But BD equals AC, therefore AB is to AC as AC is to CE. Therefore, a third proportional CE has been found to two given straight lines AB and AC.
Problem 2
To find a fourth proportional to three given straight lines.
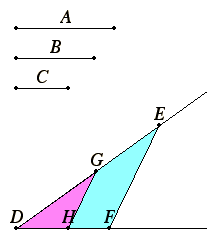
Let A and B and C be the three given straight lines. It is required to find a fourth proportional to A, B, and C. Set out two straight lines DE and DF containing any angle EDF. Make DG equal to A, GE equal to B, and DH equal to C. Join GH, and draw EF through E parallel to it. Then since GH is parallel to a side EF of the triangle DEF, therefore DG is to GE as DH is to HF. But DG equals A and GE to B, and DH to C, therefore A is to B as C is to HF. Therefore, a fourth proportional HF has been found to the three given straight lines A, B, and C.
Problem 3
To find a mean proportional to two given straight lines. Let AB and BC be the two given straight lines.
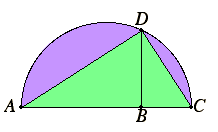
It is required to find a mean proportional to AB and BC. Place them in a straight line, and describe the semicircle ADC on AC. Draw BD from the point B at right angles to the straight line AC, and join AD and DC. Since the angle ADC is an angle in a semicircle, it is right. And, since, in the right-angled triangle ADC, BD has been drawn from the right angle perpendicular to the base, therefore BD is a mean proportional between the segments of the base, AB and BC. Therefore, a mean proportional BD has been found to the two given straight lines AB and BC.
Explore more
geometric principles
This post is part of our Guide to Euclidean Geometry. You can explore more or return to the index page to follow the series in sequential order.
Up Next
The Cuboctahedron
Sacred Geometry is defined as drawing without measurement. It involves the tools of drawing compass…