Welcome, to this online guide to Euclidean Geometry, produced by In2infinity, and written by Sunil Jenkar. In this post, we will be exploring the simple circle, and the various terminologies used in the filed of geometry.
What is a Circle?
The Circle is a fundamental geometric shape and the most aesthetic of all curves as well as the most symmetric. The construction of a circle using a compass is a granted one from the third postulate of Euclid. Circle exhibits wonderful geometric properties that are far from being trivial and have been a source of curiosity and pleasure for mathematicians for ages. For eg, of all plane shapes with a fixed perimeter (boundary) circle bounds the greatest amount of area (surface). We will explore some of these properties in this article.
Definitions
Circle: A closed curve lying in a plane, and such that all of its points are equally distant from a fixed point in the plane, is called a circle. That fixed point is called the centre.
Circle as a Locus: It follows that the locus of a point in a plane at a given distance from a fixed point is a circle.
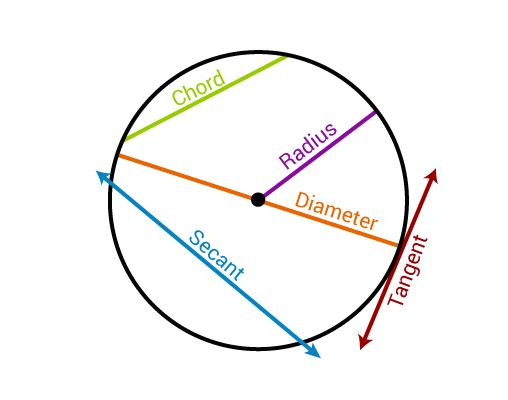
Diameter: A straight line through the centre, terminated at each end by the circle, is called a diameter. Since a diameter equals two radii, it follows that all diameters of the same circle or of equal circles are equal.
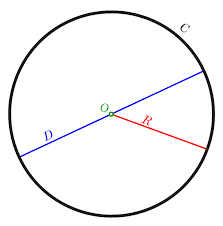
Radius: A straight line from the centre to the circle’s circumference is called a radius.
Equal Radii: It follows that all radii of the same circle or of equal circles are equal, and that all circles of equal radii are equal.
Circumference: The distance around the parameter of the circle. If the Diameter is 1 the circumference is π (pi).
Arc: Any portion of a circle is called an arc. An arc that is half of a circle is called a semicircle. An arc less than a semicircle is called a minor arc, and an arc greater than a semicircle is called a major arc. The word arc taken alone is generally understood to mean a minor arc.
Central Angle: If the vertex of an angle is at the centre of a circle and the sides are radii of the circle, the angle is called a central angle. An angle is said to intercept any arc cut off by its sides, and the arc is said to subtend the angle.
Circular Arc Theorems
- In the same circle or in equal circles equal central angles intercept equal arcs; and of two unequal central angles the greater intercepts the greater arc.
- In the same circle or in equal circles equal arcs subtend equal central angles; and of two unequal arcs the greater subtends the greater central angle.
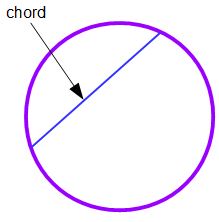
Chord
A straight line that has its extremities on a circle is called a chord. A chord is said to subtend the arcs that it cuts from a circle. Unless the contrary is stated, the chord is taken as subtending the minor arc.
In the same circle or in equal circles equal arcs subtend equal central angles; and of two unequal arcs the greater subtends the greater central angle.
Chord Theorems
In the same circle or in equal circles, if two arcs are equal, they are subtended by equal chords; and if two arcs are unequal, the greater is subtended by the greater chord.
Corollary: In the same circle or in equal circles, the greater of two unequal major arcs is subtended by the lesser chord.
In the same circle or in equal circles, if two chords are equal, they subtend equal arcs; and if two chords are unequal, the greater subtends the greater arc.
Corollary: In the same circle or in equal circles, the greater of two unequal chords subtends the less major arc.
A line through the center of a circle perpendicular to a chord bisects the chord and the arcs subtended by it.
Corollary
- A diameter bisects the circle.
- A line through the center that bisects a chord, not a diameter, is perpendicular to the chord.
- The perpendicular bisector of a chord passes through the center of the circle and bisects the arcs subtended by the chord.
- In the same circle or in equal circles equal chords are equidistant from the center, and chords equidistant from the center are equal.
- In the same circle or in equal circles, if two chords are unequal, they are unequally distant from the center, and the greater chord is at the less distance.
- In the same circle or in equal circles, if two chords are unequally distant from the center, they are unequal, and the chord at the less distance is the greater.
SECANT AND TANGENT
A straight line that intersects a circle is called a secant. A straight line of unlimited length that has one point, and only one, in common with a circle is called a tangent to the circle.
SECANT AND TANGENT THEOREMS
A line perpendicular to a radius at its extremity on the circle is tangent to the circle.
Corollary:
- A tangent to a circle is perpendicular to the radius drawn to the point of contact.
- A perpendicular to a tangent at the point of contact passes through the center of the circle.
- A perpendicular from the center of a circle to a tangent passes through the point of contact.
Concentric Circles
Two circles that have the same centre are said to be concentric.

THEOREMS
- Two parallel lines intercept equal arcs on a circle.
- Through three points not in a straight line one circle, and only one, can be drawn.
- The tangents to a circle drawn from an external point are equal, and make equal angles with the line joining the point to the centre.
Corollary:
Two circles can intersect in only two points.
If two circles have three points in common, can it be shown that they coincide and form one circle?
Tangent Circles
Line of Centres
The line determined by the centres of two circles is called the line of centres.
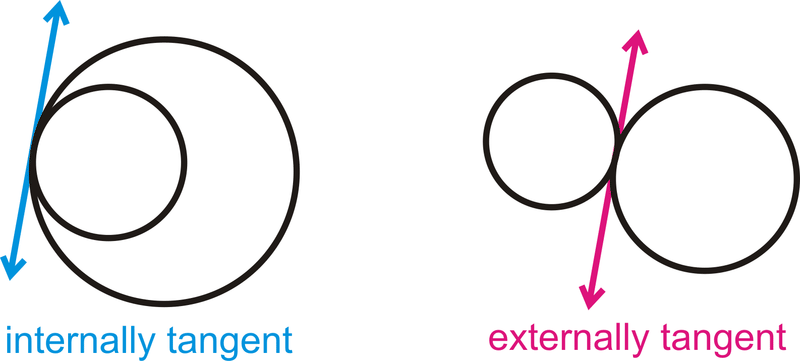
Tangent Circles
Two circles that are both tangent to the same line at the same point are called tangent circles. Circles are said to be tangent internally or externally, according as they lie on the same side of the tangent line or on opposite sides. If two circles intersect, the line of centres is the perpendicular bisector of their common chord. If two circles are tangent to each other, the line of centres passes through the point of contact.
THEOREMS
- In the same circle or in equal circles, two central angles have the same ratio as their intercepted arcs.
- An inscribed angle is measured by half the intercepted arc.
- An angle formed by two chords intersecting within the circle.is measured by half the sum of the intercepted arcs.
- An angle formed by a tangent and a chord drawn from the point of contact is measured by half the intercepted arc.
- An angle formed by two secants, a secant and a tangent, or two tangents, drawn to a circle from an external point, is measured by half the difference of the intercepted arcs.
Corollary:
- An angle inscribed in a semicircle is a right angle. For it is half of a central straight angle.
- An angle inscribed in a segment greater than a semicircle is an acute angle, and an angle inscribed in a segment less than a semicircle is an obtuse angle.
- Angles inscribed in the same segment or in equal segments are equal.
- If a quadrilateral is inscribed in a circle, the opposite angles are supplementary; and, conversely, if two opposite angles of a quadrilateral are supplementary, the quadrilateral can be inscribed in a circle.
Euclidean Construction
There are some mathematical proofs which arise out of compass construction based on the principles of Eucldean Geometry.
To find the centre of a given circle.
Let ABC be the given circle. It is required to find the centre of the circle ABC.
Draw a straight line AB through it at random, and bisect it at the point D. Draw DC from D at right angles to AB, and draw it through to E. Bisect CE at F. I say that F is the centre of the circle ABC.
For suppose it is not, but, if possible, let G be the centre. Join GA, GD, and GB. Then, since AD equals DB, and DG is common, the two sides AD and DG equal the two sides BD and DG respectively. And the base GA equals the base GB, for they are radii, therefore the angle ADG equals the angle GDB.
But, when a straight line standing on a straight line makes the adjacent angles equal to one another, each of the equal angles is right, therefore the angle GDB is right. But the angle FDB is also right, therefore the angle FDB equals the angle GDB, the greater equals the less, which is impossible. Therefore, G is not the centre of the circle ABC. Similarly, we can prove that neither is any other point except F. Therefore, the point F is the centre of the circle ABC.
From a given point to draw a straight line touching a given circle.
Let A be the given point, and BCD the given circle. It is required to draw from the point A, a straight line touching the circle BCD. Take the centre E of the circle, and join AE. Describe the circle AFG with centre E and radius EA. Draw DF from D at right angles to EA. Join EF and AB. I say that AB has been drawn from the point A touching the circle BCD.
For, since E is the centre of the circles BCD and AFG, EA equals EF, and ED equals EB. Therefore, the two sides AE and EB equal the two sides FE and ED, and they contain a common angle, the angle at E, therefore the base DF equals the base AB, and the triangle DEF equals the triangle BEA, and the remaining angles to the remaining angles, therefore the angle EDF equals the angle EBA.
But the angle EDF is right, therefore the angle EBA is also right. Now EB is a radius, and the straight line drawn at right angles to the diameter of a circle, from its end, touches the circle, therefore AB touches the circle BCD. Therefore, from the given point A the straight line AB has been drawn touching the circle BCD.
Given a segment of a circle, to describe the complete circle of which it is a segment.
Let ABC be the given segment of a circle. It is required to describe the complete circle belonging to the segment ABC, that is, of which it is a segment. Bisect AC at D, draw DB from the point D at right angles to AC, and join AB. The angle ABD is then greater than, equal to, or less than the angle BAD.
First, let it be greater. Construct the angle BAE on the straight line BA, and at the point A on it, equal to the angle ABD. Draw DB through to E, and join EC. Then, since the angle ABE equals the angle BAE, the straight line EB also equals EA.
And, since AD equals DC, and DE is common, the two sides AD and DE equal the two sides CD and DE respectively, and the angle ADE equals the angle CDE, for each is right, therefore the base AE equals the base CE.
But AE was proved equal to BE, therefore BE also equals CE. Therefore, the three straight lines AE, EB, and EC equal one another. Therefore, the circle drawn with centre E and radius one of the straight lines AE, EB, or EC also passes through the remaining points and has been completed. Therefore, given a segment of a circle, the complete circle has been described.
Advanced Geometry
There are some mathematical proofs which arise out of compass construction based on the principles of Eucldean Geometry.
INVERSE POINTS
Two points collinear with the centre of a given circle and the product of whose distances from the centre is equal to the square of the radius are said to be inverse points with respect to, or for, the circle.
Two inverse points lie on the same side of the centre of the circle. Of two inverse points, one lies inside and the other outside the circle. If a point is taken on the circle, its inverse coincides with the point considered.
Properties of Inverse Points
- Two inverse points divide the corresponding diameter harmonically.
- The ratio of the distances of a variable point of a circle from two given inverse points is constant.
ORTHOGONAL CIRCLES
Two circles are said to be orthogonal if the square of their line of centres is equal to the sum of the squares of their radii.
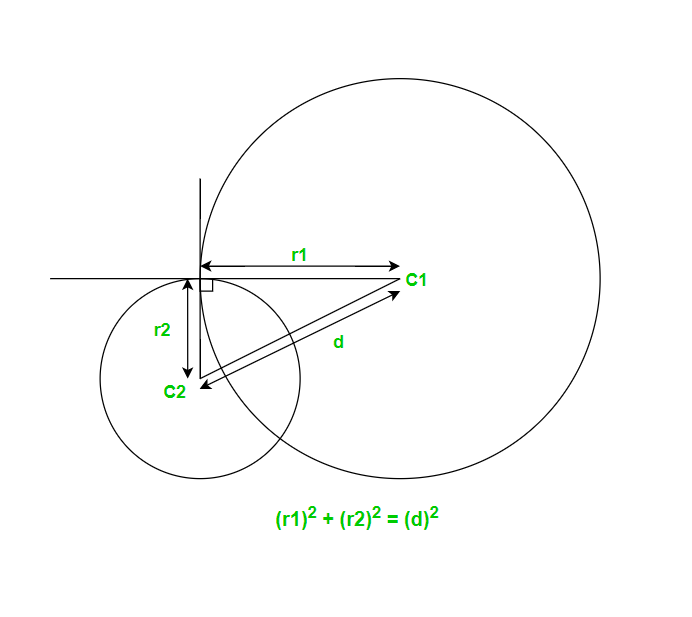
Properties of Orthogonal Circles
- In two orthogonal circles, the two radii passing through a common point of the two circles are rectangular. Conversely, If the two radii passing through a point common to two circles are rectangular, the two circles are orthogonal.
- If two circles are orthogonal, the radius of one circle passing through a point common to the two circles is tangent to the second circle. Conversely, given two intersecting circles, if the radius of one circle passing through a point common to the two circles is tangent to the second circle, the two circles are orthogonal.
- If two circles are orthogonal, any two points of one of them collinear with the centre of the second circle are inverse for that second circle. Conversely, If two points of one circle are inverse for a second circle, the two circles are orthogonal.
- The two lines joining the points of intersection of two orthogonal circles to a point on one of the circles meet the other circle in two diametrically opposite points.
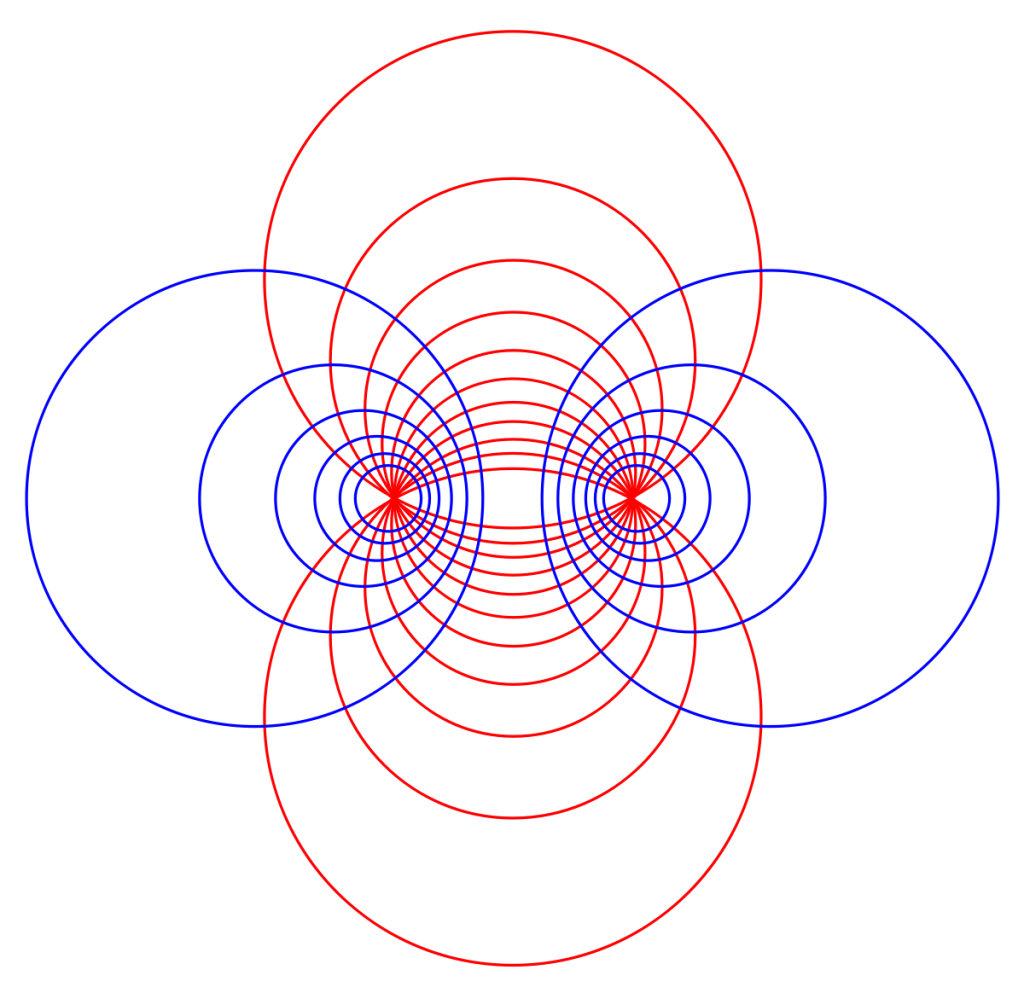
Circle of Apollonius
The great Greek geometer, Apollonius of Perga, showed that a circle may also be defined as the set of points in a plane having a constant ratio (other than 1) of distances to two fixed foci, A and B. Given two points A and B and a number r. What is the locus of points P such that AP/BP=r? Surprisingly, the answer is a circle. The circle, which is known as the Apollonian Circle. For every positive r there is a different one.
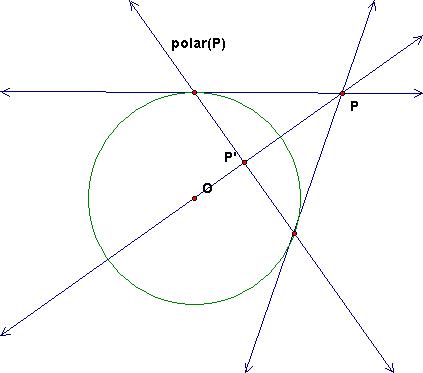
POLES AND POLARS
The harmonic conjugate of a fixed point with respect to a variable pair of points which lie on a given circle and are collinear with the fixed point, describes a straight line. The line is said to be the polar line of the point with respect to, or for, the circle, and the point is said to be the pole of the line.
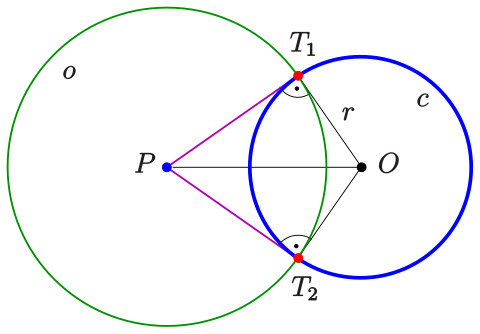
THE POWER OF A POINT WITH RESPECT TO A CIRCLE
The product of the distances of a given point, taken either inside or outside a given circle, from any two points which are collinear with the given point and lie on the circle, is a constant. The constant is called the power of the point with respect to the circle, or, more briefly, for the circle.
THE RADICAL AXIS OF TWO CIRCLES
The locus of a point which moves so that its powers with respect to two given circles are equal is a straight line perpendicular to the line of centres of the given circles. The line is called the radical axis or, briefly, the axis of the two circles.
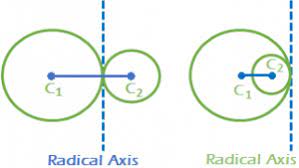
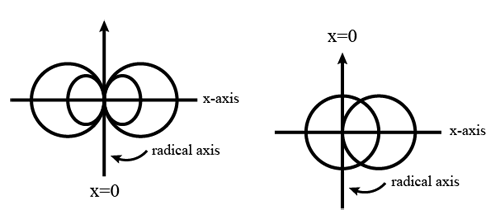
COAXIAL CIRCLES
A group of circles are said to form a coaxial pencil, if the same fixed line is the radical axis of any two of the circles of the group. The fixed line is called the radical axis, or, more briefly, the axis of the coaxial pencil.
Explore more
geometric principles
This post is part of our Guide to Euclidean Geometry. You can explore more or return to the index page to follow the series in sequential order.
Up Next

Similarity
Welcome, to this online guide to Euclidean Geometry, produced by In2infinity, and written by Sunil…






