What is a Polygon?
The figure formed by a non-self-intersecting closed broken line together with the part of the plane bounded by this line is called a polygon. The sides and vertices of this broken line are called respectively sides and vertices of the polygon, and the angles formed by each two adjacent sides (interior) angles of the polygon. The smallest number of sides in a polygon is three. Polygons are named according to the number of their sides: triangles, quadrilaterals, pentagons, hexagons, and so on.
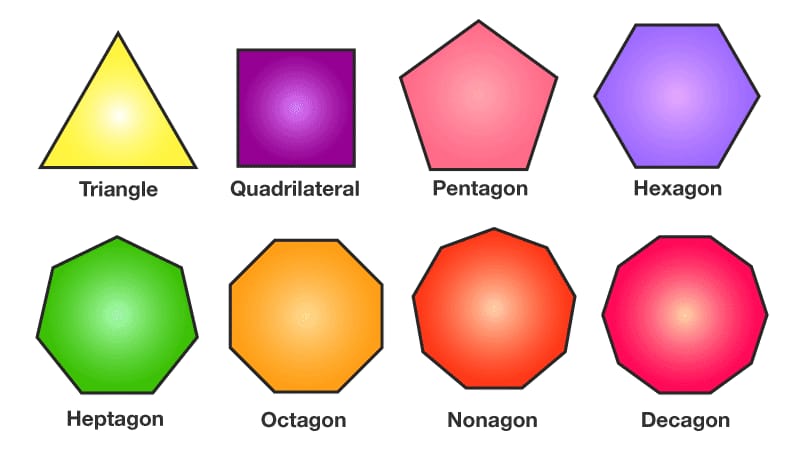
The Triangle
The Triangle is a geometrical figure that is contained by three straight lines. Every triangle has three sides and three angles. It is the most basic as well as the most important shape. Triangle is a prime figure, prime figure is one which cannot be divided into any other figures more simple then itself. Triangle serves as a basis to understand all other geometrical figures and their properties. The reason being that the triangle is the only rigid figure among all polygons as there is no scope for “wiggling” unlike all other higher polygons, a triangle can be completely defined using the least number of parameters.
Classification of Triangles
Triangles are generally classified according to type of sides and/or angles. All triangles fall into
Triangle classification according to type of sides:
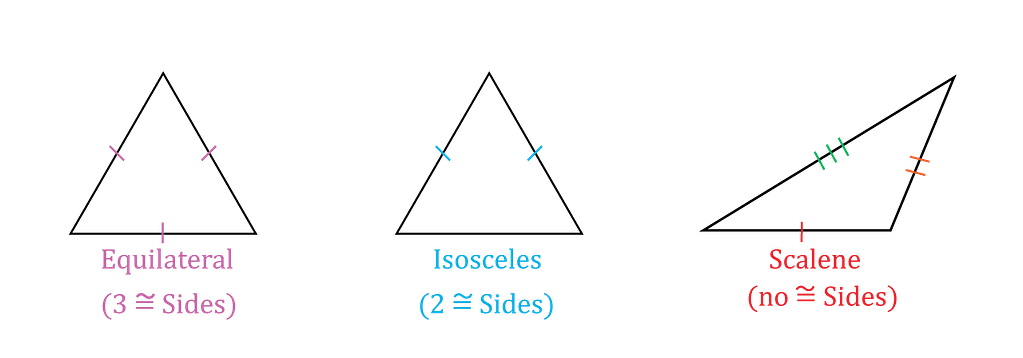
- Equilateral: The triangles which have all sides of equal in length.
- Isosceles: The triangles which have two of the sides of equal in length.
- Scalene: The triangles which have all sides of different lengths.
Triangle classification according to type of angles:
- Acute: A triangle is said to be acute when all of its angles are acute angles.
- Obtuse: A triangle is said to be obtuse when one of its angles is an obtuse angle.
- Right: A triangle is said to be right when one of its angles is a right angle.
Congruence
Geometrical objects are said to be congruent when they have the same shape and size. ‘Congruent’ can be understood as the geometrical equivalent of the common term ‘equal’. two geometric figures are called congruent if they can be identified with each other by superimposing.
Congruent and non-congruent segments
Two segments are congruent if they can be laid one onto the other so that their endpoints coincide.
Congruent and non-congruent angles
In accordance with the general definition of congruent figures two angles are considered congruent if by moving one of them it is possible to identify it with the other.
Congruence of Triangles
The necessary and sufficient conditions to decide congruence in case of triangles are as follows:
- SAS (Side-Angle-Side): Two triangles are congruent if two sides and the included angle of the one are equal respectively to two sides and the included angle of the other.
- SSS (Side-Side-Side): Two triangles are congruent if the three sides of the one are equal respectively to the three sides of the other.
- ASA (Angle-Side-Angle): Two triangles are congruent if two angles and the included side of the one are equal respectively to two angles and the included side of the other. ASA automatically implies AAS or SAA congruence. Hence the theorem can be rephrased as, If two triangles have two angles equal to two angles respectively, and one side equal to one side, namely, either the side adjoining the equal angles, or that opposite one of the equal angles, then the remaining sides equal the remaining sides and the remaining angle equals the remaining angle.
- RHS (Right-angle-Hypotenuse-Side): Two right triangles are congruent if the hypotenuse and a side of the one are equal respectively to the hypotenuse and a side of the other.
Important lines in a triangle
One of a triangle’s sides is often referred to as the base, in which case the opposite vertex is called the vertex of the triangle, and the other two sides are called lateral. Any triangle has three altitudes, three medians, and three bisectors, since each side of the triangle can take on the role of the base.
Locus
The path of a point that moves in accordance with certain given geometric conditions is called the locus of the point.
Altitude
The perpendicular dropped from the vertex to the base or to its continuation is called an altitude.
Perpendicular Bisector
A line that bisects a given line and is perpendicular to it is called the perpendicular bisector of the line. In other words, the locus of a point equidistant from the extremities of a given line is the perpendicular bisector of that line.
Corollary
- Two points each equidistant from the extremities of a line determine the perpendicular bisector of the line.
- The locus of a point equidistant from two given intersecting lines is a pair of lines bisecting the angles formed by those lines.
Median
A line from any vertex of a triangle to the midpoint of the opposite side is called a median of the triangle.
Concurrent Lines
If two or more lines pass through the same point, they are called concurrent lines.
- The bisectors of the angles of a triangle are concurrent in a point equidistant from the sides of the triangle.
- The perpendiculars from the vertices of a triangle to the opposite sides are concurrent.
- The medians of a triangle are concurrent in a point two thirds of the distance from each vertex to the middle of the opposite side.
Angle Sum Property
The sum of the three angles of a triangle is equal to two right angles.
Corollary
- If two triangles have two angles of the one equal to two angles of the other, the third angles are equal.
- In a triangle there can be but one right angle or one obtuse angle.
Triangle Theorems
Triangle Inequality Theorems
- The sum of any two sides of a triangle is greater than the third side, and the difference between any two sides is less than the third side.
- If two sides of a triangle are unequal, the angles opposite these sides are unequal, and the angle opposite the greater side is the greater.
- If two angles of a triangle are unequal, the sides opposite these angles are unequal, and the side opposite the greater angle is the greater.
- If two triangles have two sides of the one equal respectively to two sides of the other, but the included angle of the first triangle greater than the included angle of the second, then the third side of the first is greater than the third side of the second.
- If two triangles have two sides of the one equal respectively to two sides of the other, but the third side of the first triangle greater than the third side of the second, then the angle opposite the third side of the first is greater than the angle opposite the third side of the second.
Exterior Angle Theorems
- In any triangle, if one of the sides is produced, then the exterior angle is greater than either of the interior and opposite angles.
- In any triangle, if one of the sides is produced, then the exterior angle equals the sum of the two interior and opposite angles, and the sum of the three interior angles of the triangle equals two right angles.
Triangle and Parallel lines Theorems
- Triangles which are on the same base and in the same parallels equal one another.
- Triangles which are on equal bases and in the same parallels equal one another.
- Equal triangles which are on the same base and on the same side are also in the same parallels.
- Equal triangles which are on equal bases and on the same side are also in the same parallels.
Pythagoras Theorem
In right-angled triangles the square on the side opposite the right angle equals the sum of the squares on the sides containing the right angle. Conversely, If in a triangle the square on one of the sides equals the sum of the squares on the remaining two sides of the triangle, then the angle contained by the remaining two sides of the triangle is right.
Explore more
geometric principles
This post is part of our Guide to Euclidean Geometry. You can explore more or return to the index page to follow the series in sequential order.
Up Next
Polygon
Welcome, to this online guide to Euclidean Geometry, produced by In2infinity, and written by Sunil…
