Welcome, to this online guide to Euclidean Geometry, produced by In2infinity, and written by Sunil Jankar. In this final section we examine the nature of cylinders and cones.
Surfaces of Revolution
A surface of revolution is the surface obtained by rotating any curve, called a generatrix (or generator) about a fixed line, called the axis of revolution. On the generatrix, take any point and drop from it the perpendicular to the axis.
Obviously, in the process of rotation of the generatrix about the axis, the angle (of the genetrix curve with respect to the axis of revolution), the length of the perpendicular, and the position of its foot remain unchanged.
Therefore, each point of the generatrix describes a circle, the plane of which is perpendicular to the axis of revolution, and the center of which is the intersection of this plane with the axis.
Thus, the cross section of a surface of revolution by a plane perpendicular to the axis consists of one or several circles. Any plane containing the axis of revolution is called meridional, and the cross section of the surface by this plane a meridian. All meridians of a given surface of revolution are congruent to each other, because in the process of revolution each of them assumes the positions of every other meridian.

Cylinders
Cylindrical Surface
A surface generated by a straight line which is constantly parallel to a fixed straight line, and touches a fixed curve not in the plane of the straight line, is called a cylindrical surface.
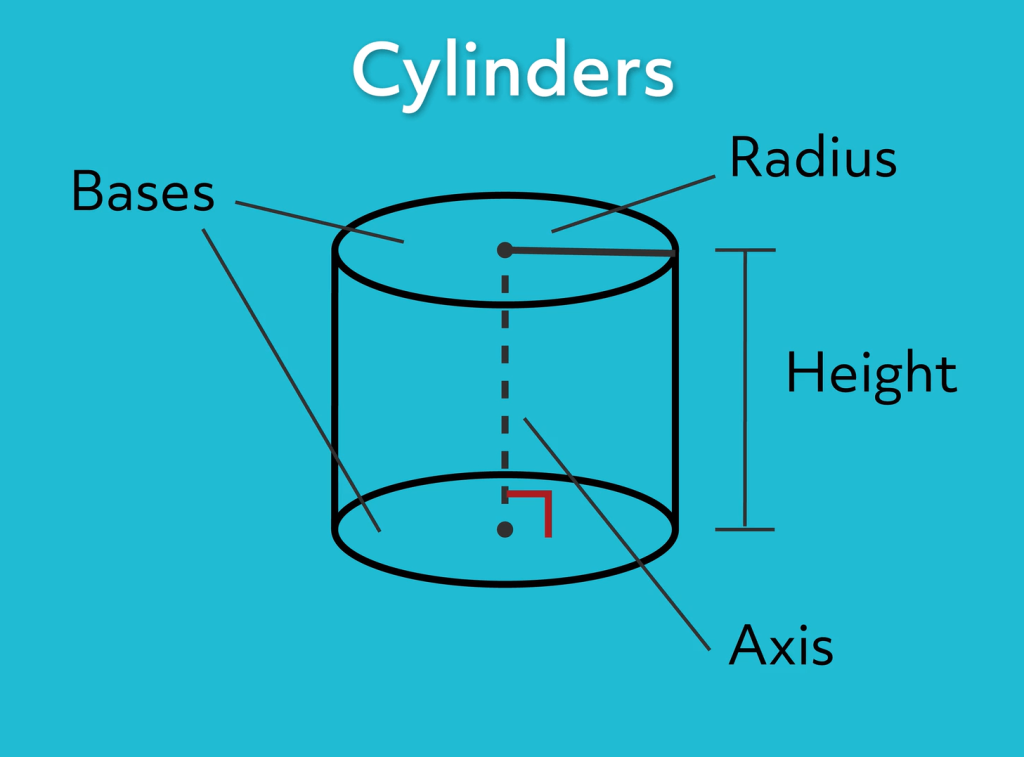
Cylinder
A solid bounded by a cylindrical surface and two parallel plane surfaces is called a cylinder.
The part of the cylindrical surface contained between the planes is called the lateral surface, and the parts of the planes cut out by this surface bases of the cylinder. A perpendicular dropped from any point of one base to the plane of the other is called an altitude of the cylinder.
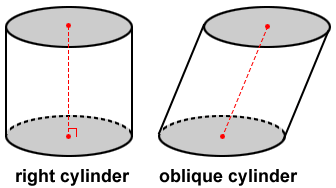
Right and Oblique Cylinders
A cylinder whose elements are perpendicular to its bases is called a right cylinder; otherwise a cylinder is called an oblique cylinder.
Section of a Cylinder
A figure formed by the intersection of a plane and a cylinder is called a section of the cylinder.
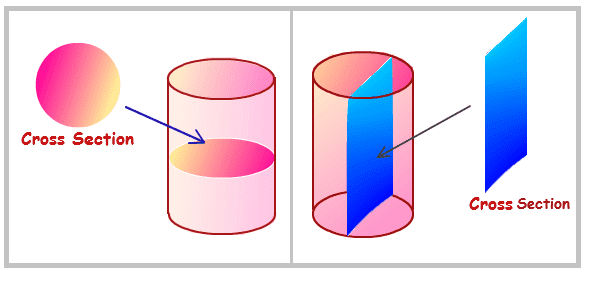
PROPOSITION XX
Every section of a cylinder made by a plane passing through an element is a parallelogram
Corollary
Every section of a right cylinder made by a plane passing through an element is a rectangle.
Circular Cylinder
A cylinder whose bases are circles is called a circular cylinder. A right circular cylinder, being generated by the revolution of a rectangle about one side as an axis, is also called a cylinder of revolution.
In our elementary exposition, we will consider only right circular cylinders, and for the sake of brevity refer to them simply as cylinders. Sometimes we will deal with prisms whose bases are polygons inscribed into the bases of a cylinder, or circumscribed about them, and the altitudes are congruent to the altitude of the cylinder. We will call such prisms inscribed into (respectively circumscribed about) the cylinder.
PROPOSITION II
The bases of a cylinder are congruent.
Corollary
- Any two parallel sections of a cylinder, cutting all the elements, are congruent.
- Any section of a cylinder parallel to the base is congruent to the base.
- The straight line joining the centers of the bases of a circular cylinder passes through the centers of all sections of the cylinder parallel to the bases.
Tangent Plane
A plane which contains an element of a cylinder, but does not cut the surface, is called a tangent plane to the cylinder.
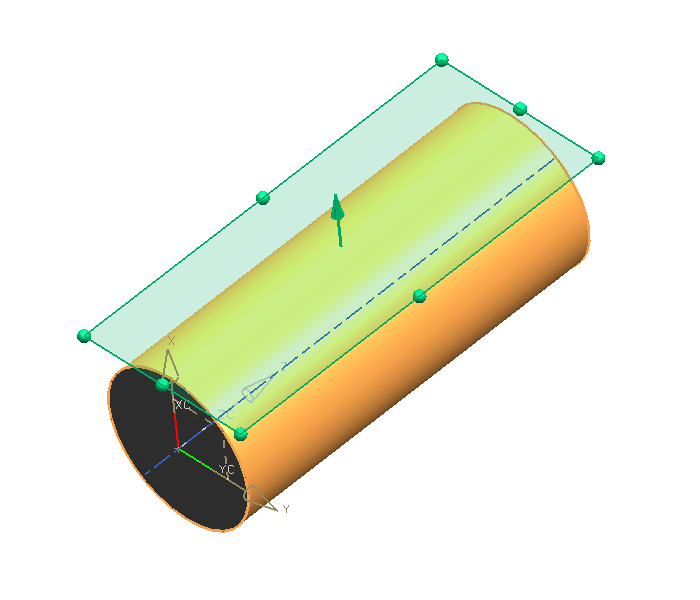
Construction of Tangent Planes
From a consideration of the nature of a tangent plane and of the construction of a cylindrical surface it is evident that:
- A plane passing through a tangent to the base of a circular cylinder and the element drawn through the point of contact is tangent to the cylinder.
- If a plane is tangent to a circular cylinder, its intersection wIth the plane of the base is tangent to the base.
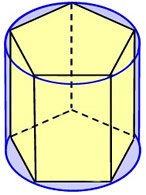
Inscribed Prism
A prism whose lateral edges are elements of a cylinder and whose bases are inscribed in the bases of the cylinder is called an inscribed prism. In this case the cylinder is said to be circumscribed about the prism.
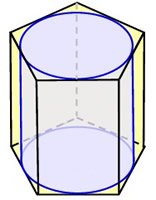
Circumscribed Prism
A prism whose lateral faces are tangent to the lateral surface of a cylinder and whose bases are circumscribed about the bases of the cylinder is called a circumscribed prism. In this case the cylinder is said to be inscribed in the prism.
Right Section
A section of a cylinder made by a plane that cuts all the elements and is perpendicular to them is called a right section of the cylinder.

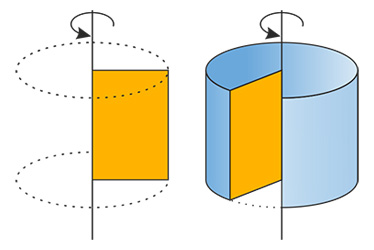
Cylinder as a Limit
If a prism whose base is a regular polygon is inscribed in or circumscribed about a circular cylinder, and if the number of sides of the prism is indefinitely increased,
- The volume of the cylinder is the limit of the volume of the prism.
- The lateral area of the cylinder is the limit of the lateral area of the prism.
- The perimeter of a right section of the cylinder is the limit of the perimeter of a right section of the prism.
For as we increase the number of sides of the base of the inscribed or circumscribed prism whose base is a regular polygon, the perimeter of the base approaches the circle as its limit.
This brings the lateral surface of each prism nearer and nearer the lateral surface of the cylinder. It also brings the volume of each prism nearer and nearer the volume of the cylinder. In the same way it brings the right section of each prism nearer and nearer the right section of the cylinder.

PROPOSITION III
The lateral area of a circular cylinder is equal to the product of an element by the perimeter of a right section of the cylinder.
Corollary
The lateral area of a cylinder of revolution is equal to the product of the altitude by the circumference of the base. In the case of a right circular cylinder of altitude a, lateral area l, total area t, and radius of base r, we have I = 2πra, and t = πra + 2πr² = 2πr (a + r).
PROPOSITION IV
The volume of a circular cylinder is equal to the product of its base by its altitude.
Corollary
The volume of a cylinder of revolution with radius r and altitude a is ????r²a.
Similar Cylinders
Cylinders generated by the revolution of similar rectangles about corresponding sides are called similar cylinders of revolution.
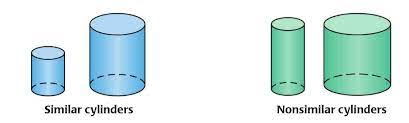
PROPOSITION V
The lateral areas, or the total areas, of similar cylinders of revolution are to each other as the squares of their altitudes or as the squares of their radii; and their volumes are to each other as the cubes of their altitudes or as the cubes of their radii.
Conic Surface
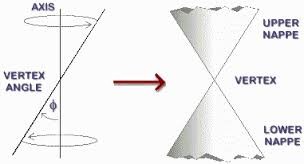
A surface generated which constantly touches a fixed plane through a fixed point not in the plane of the curve is called a conic surface or a conical surface. The moving line is called the generatrix, the fixed curve the directrix, and the fixed point the Vertex.

Element
The generatrix in any position is called an element of the conic surface. If the generatrix is of indefinite length, the surface consists of two portions, one above and the other below the vertex, which are called the upper nappe and lower nappe respectively.
Cone
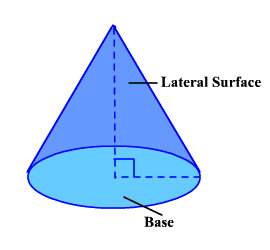
A solid bounded by a conic surface and a plane cutting all the elements is called a cone.
The conic surface is called the lateral surface of the cone, and the plane surface is called the base of the cone. The vertex of the conic surface is called the vertex of the cone, and the elements of the conic surface are called the elements of the cone. The perpendicular distance from the vertex to the plane of the base is called the altitude of the cone.
Circular Cone
A cone whose base is a circle is called a circular cone. The straight line joining the vertex of a circular cone and the center of the base is called the axis of the cone.
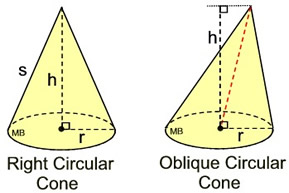
Right and Oblique Cones
A circular cone whose axis is perpendicular to the base is called a right cone; otherwise a circular cone is called an oblique cone.
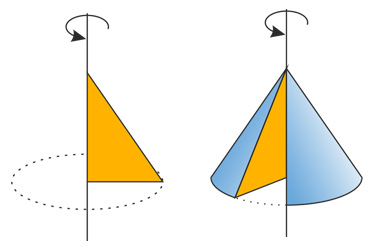
Cone of Revolution
Since a right circular cone may be generated by the revolution of a right triangle about one of the sides of the right angle, it is called a cone of revolution. In this case the hypotenuse corresponds to an element of the surface and is called the slant height. We will consider only right circular cones and refer to them simply as cones for the sake of brevity. Sometimes we will consider pyramids whose vertices coincide with the vertex of a given cone, and bases are inscribed into, or circumscribed about its base. We will call such pyramids inscribed into the cone, and respectively circumscribed about it.
Conic Section
A section formed by the intersection of a plane and the conic surface of a cone of revolution is called a conic section.
PROPOSITION VI
Every section of a cone made by a plane passing through its vertex is a triangle.
PROPOSITION VII
In a circular cone a section made by a plane parallel to the base is a circle.
Corollary
The axis of a circular cone passes through the center of every section which is parallel to the base.
Tangent Plane
A plane which contains an element of a cone, but does not cut the surface, is called a tangent plane to the cone.
Construction of Tangent Planes
It is evident that:
- A plane passing through a tangent to the base of a circular cone and the element drawn through the point of contact is tangent to the cone.
- If a plane is tangent to a circular cone its intersection with the plane of the base is tangent to the base.
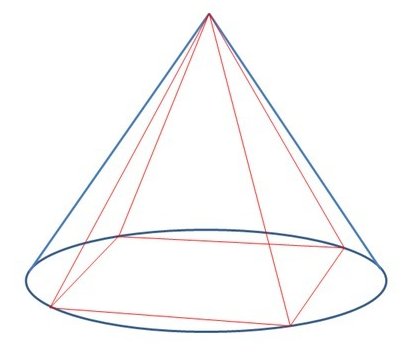
Inscribed Pyramid
A pyramid whose lateral edges are elements of a cone and whose base is inscribed in the base of the cone is called an inscribed pyramid. In this case the cone is said to be circumscribed about the pyramid.
Circumscribed Pyramid
A pyramid whose lateral faces are tangent to the lateral surface of a cone and whose base is circumscribed about the base of the cone is called a circumscribed pyramid. In this case the cone is said to be inscribed in the pyramid.
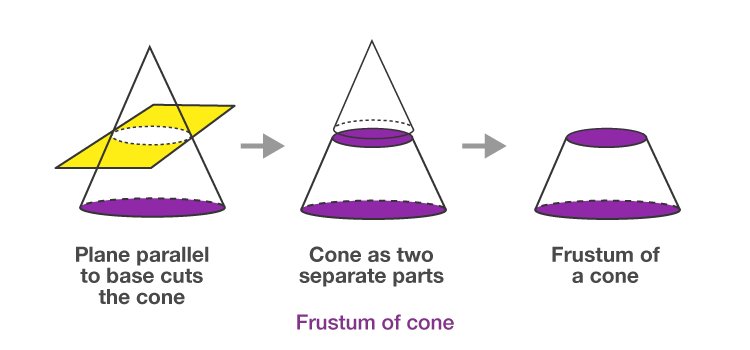
Frustum of a Cone
The portion of a cone included between the base and a section parallel to the base is called a frustum of a cone. The base of the cone and the parallel section are together called the bases of the frustum. The terms altitude and lateral area of a frustum of a cone, and slant height of a frustum of a right circular cone, are used in substantially the same manner as with the frustum of a pyramid.
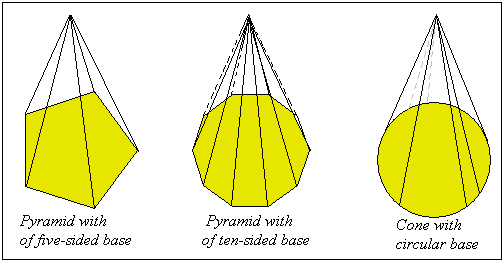
Cones and Frustums as Limits
If a pyramid whose base is a regular polygon is inscribed in or circumscribed about a circular cone, and if the number of sides of the base of the pyramid is indefinitely increased, the volume of the cone is the limit of the volume of the pyramid, and the lateral area of the cone is the limit of the lateral area of the pyramid. The volume of a frustum of a cone is the limit of the volumes of the frustums of the inscribed and circumscribed pyramids, if the number of lateral faces is indefinitely increased, and the lateral area of the frustum of a cone is the limit of the lateral areas of the frustums of the inscribed and circumscribed pyramids, the bases being regular polygons.
PROPOSITION VIII
The lateral area of a cone of revolution is equal to half the product of the slant height by the circumference of the base.
Corollary
If I denotes the lateral area, t the total (area, s the slant height, and r the radius of the base of a cone of revolution, then:
l = ½ (2πr x s) = πrs
t = πrs + πr² = πr (s + r)
PROPOSITION IX
The volume of a circular cone is equal to one third the product of its base by its altitude.
Corollary
In a circular cone of radius r and altitude a, v = ⅓ πr²a. For the area of the base is πr².
Similar Cones
Cones generated by the revolution of similar right triangles about corresponding sides are called similar cones of revolution.
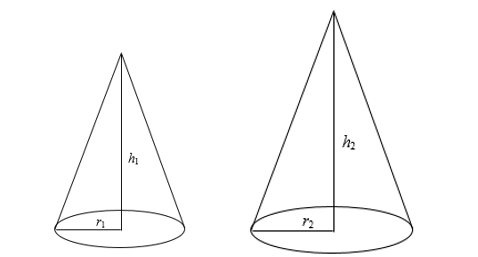
PROPOSITION X
The lateral areas, or the total areas, of two similar cones of revolution are to each other as the squares of their altitudes, as the squares of their radii, or as the squares of their slant heights; and their volumes are to each other as the cubes of their altitudes, as the cubes of their radii, or as the cubes of their slant heights.
PROPOSITION XI
The lateral area of a frustum of a cone of revolution is equal to half the sum of the circumferences of its bases multiplied by the slant height.
Corollary
The lateral area of a frustum of a cone of revolution is equal to the circumference of a section equidistant from its bases multiplied by its slant height.
PROPOSITION XII
A frustum of a circular cone is equivalent to the sum of three cones whose common altitude is the altitude of the frustum and whose bases are the lower base, the upper base, and the mean proportional between the bases of the frustum. Given frustum of a circular cone, with volume v, bases b and b’ and altitude a,
v = ⅓ a (b + b’ + √bb’)
Corollary
In a frustum of a cone of revolution, r and r’ being the radii of the bases,
v = ⅓ πa (r² + r’² + rr’)
MORE ON SECTIONS OF CONE
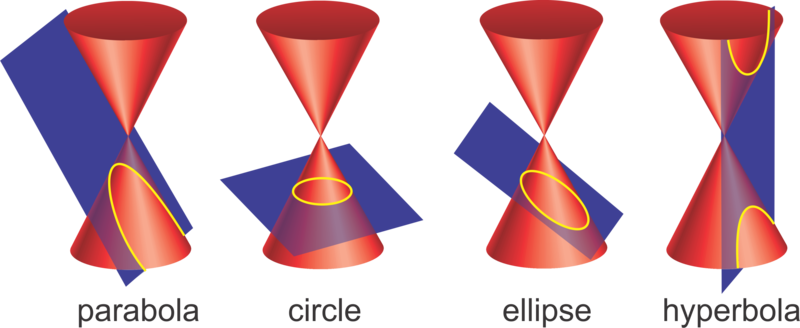
In geometry, conic section, also called conics, is any curve produced by the intersection of a plane and a right circular cone. Depending on the angle of the plane relative to the cone, the intersection is a circle, an ellipse, a hyperbola, or a parabola.
- Circle : If the cone is sliced parallel to the base, the resulting curve is a circle.
- Ellipse: If the cone is sliced on a slight angle, the curve is called an ellipse.
- Parabola : If the slice is made parallel to the edge of the cone, the curve formed is called a parabola.
- Hyperbola: If the slice is perpendicular to the base of the cone, the curve is one of two branches of a hyperbola.

The various curves derived from sections of cones hold a very special place in the study of mathematics. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga’s systematic work on their properties.
Explore more
geometric principles
This post is part of our Guide to Euclidean Geometry. You can explore more or return to the index page to follow the series in sequential order.
Up Next
Polygons II
Welcome, to this online guide to Euclidean Geometry, produced by In2infinity, and written by Sunil…







