Welcome, to this online guide to Euclidean Geometry, produced by In2infinity, and written by Sunil Jankar. In this section, we examine the geometric principles of Prisms and Pyramids.
What is a Polyhedron?
A polyhedron is a geometric solid bounded by polygons. The plural of polyhedron is polyhedra. The boundary polygons of a polyhedron are called its faces. A common side of two adjacent faces is called an edge of the polyhedron. When several faces meet at their common vertex, they form a polyhedral angle, and the vertex of the angle is called a vertex of the polyhedron. A straight segment connecting any two vertices, which do not lie in the same face, is called a diagonal of the polyhedron. The smallest number of faces a polyhedron can have is four. Such a polyhedron can be cut out of a trihedral angle by a plane. If a plane passes through a polyhedron, the intersection of the plane with such faces as it cuts is called a section of the polyhedron. If every section of a polyhedron is a convex polygon, the polyhedron is said to be convex. We will consider only those polyhedra which are convex, i.e. lie on one side of the plane of each of its faces.
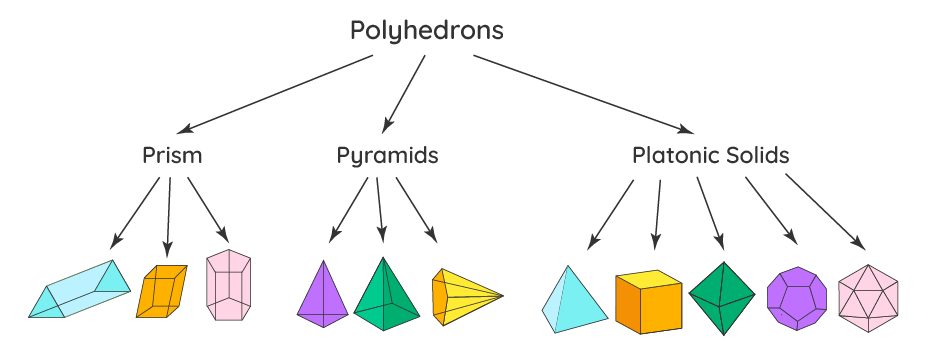
Prisms
A polyhedron of which two faces are congruent polygons in parallel planes, the other faces being parallelograms, is called a prism. The parallel polygons are called the bases of the prism, the parallelograms are called the lateral faces, and the intersections of the lateral faces are called the lateral edges.
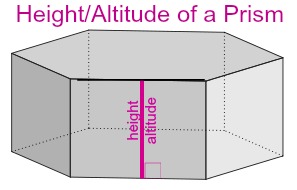
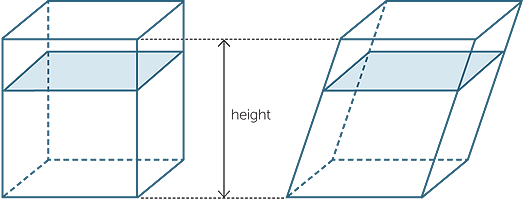
Altitude of a Prism
The perpendicular distance between the planes of the bases of a prism is called its altitude.
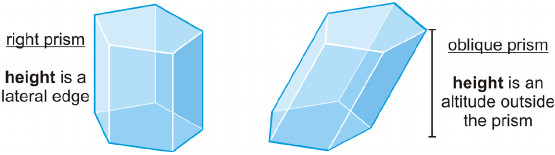
Right Prism
A prism whose lateral edges are perpendicular to its bases is called a right Prism. The lateral edges of a right prism are equal to the altitude.
Oblique Prism
A prism whose lateral edges are oblique to its bases is called an oblique prism.
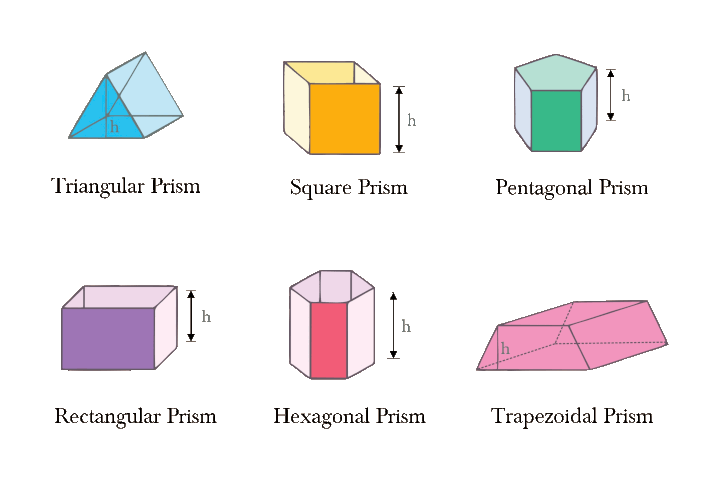
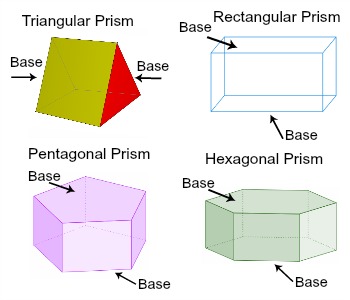
Prisms classified as to Bases
Prisms are said to be triangular, quadrangular, and so on, according as their bases are triangles, quadrilaterals, and so on.
Right Section
A section of a prism made by a plane cutting all the lateral edges. and perpendicular to them is called a right Section.

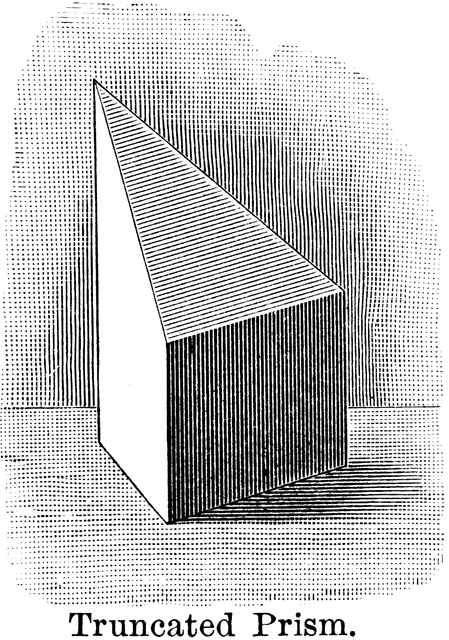
Truncated Prism
The part of a prism included between the base and a section made by a plane oblique to the base is called a truncated prism.
PROPOSITION I
The sections of a prism made by parallel planes cutting all the lateral edges are congruent polygons.
Corollary
Every section of a prism made by a plane parallel to the base is congruent to the base; and all right sections of a prism are congruent.
PROPOSITION II
The lateral area of a prism is equal to the product of a lateral edge by the perimeter of a right section.
Corollary
The lateral area of a right prism is equal to the product of the altitude by the perimeter of the base.
PARALLELEPIPED
A prism whose bases are parallelograms is called a parallelepiped.
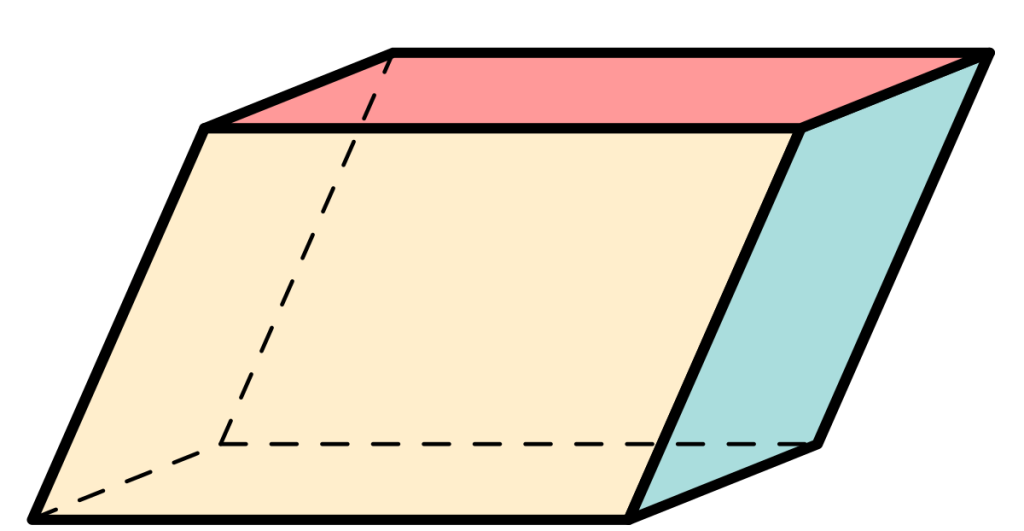
Right Parallelepiped
A parallelepiped whose edges are perpendicular to the bases is called a right parallelepiped.
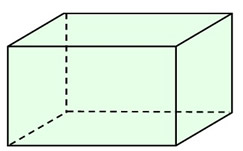
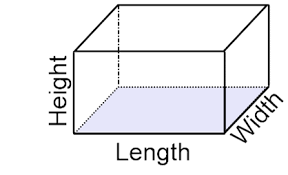
Rectangular Parallelepiped
A right parallelepiped whose bases are rectangles is called a rectangular parallelepiped.
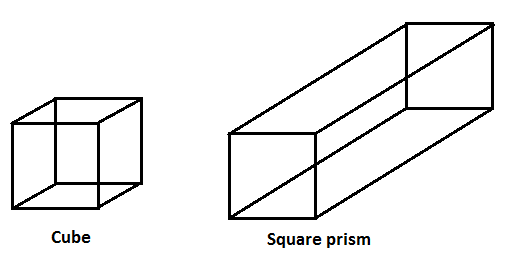
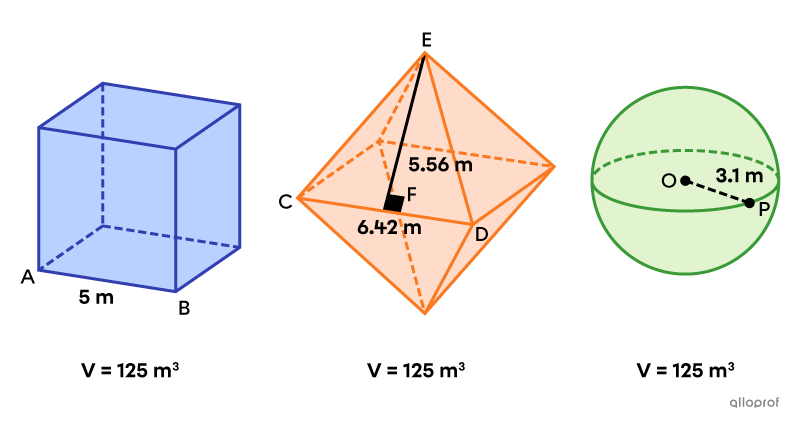
Cube
A parallelepiped whose six faces are all squares is called a cube. We might also say that a hexahedron whose six faces are all squares is a cube, because such a figure would necessarily be a parallelepiped.
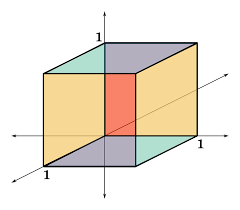
Unit of Volume
In measuring volumes, a cube whose edges are all equal to the unit of length is taken as the unit of volume.
Volume
The number of units of volume contained by a solid is called its volume.
Equivalent Solids
If two solids have equal volumes, they are said to be equivalent.
Congruent Solids
If two geometric solids are equal in all their parts, and their parts are similarly arranged, the solids are said to be congruent.
PROPOSITION III
Two prisms are congruent if the three faces which include a trihedral angle of the one are respectively congruent to three faces which include a trihedral angle of the other, and are similarly placed.
Corollary
- Two truncated prisms are congruent under the conditions given in Proposition III
- Two right prisms having congruent bases and equal altitudes are congruent.
PROPOSITION IV
An oblique prism is equivalent to a right prism whose base is equal to a right section of the oblique prism and whose altitude is equal to a lateral edge of the oblique prism.
PROPOSITION V
The opposite faces of a parallelepiped are congruent and parallel.
PROPOSITION VI
The plane passed through two diagonally opposite edges of a parallelepiped divides the parallelepiped into two equivalent triangular prisms.
PROPOSITION VII
Two rectangular parallelepipeds having congruent bases are to each other as their altitudes.
Dimensions
The lengths of the three edges of a rectangular parallelepiped which meet at a common vertex are called its dimensions.
Corollary
Two rectangular parallelepipeds which have two dimensions in common are to each other as their third dimensions.
PROPOSITION VIII
Two rectangular parallelepipeds having equal altitudes are to each other as their bases.
Corollary
Two rectangular parallelepipeds which have one dimension in common are to each other as the products of their other two dimensions.
PROPOSITION IX
Two rectangular parallelepipeds are to each other as the products of their three dimensions.
Corollary
- The volume of a rectangular parallelepiped is equal to the product of its three dimensions.
- The volume of a rectangular parallelepiped is equal to the product of its base and altitude.
PROPOSITION X
The volume of any parallelepiped is equal to the product of its base by its altitude.
Corollary
The volume of any parallelepiped is equal to that of a rectangular parallelepiped of equivalent base and equal altitude.
PROPOSITION XI
The volume of a triangular prism is equal to the product of its base by its altitude.
PROPOSITION XII
The volume of any prism is equal to the product of its base by its altitude.
Corollary
- Prisms having equivalent bases are to each other as their altitudes; prisms having equal altitudes are to each other as their bases.
- Prisms having equivalent bases and equal altitudes are equivalent.
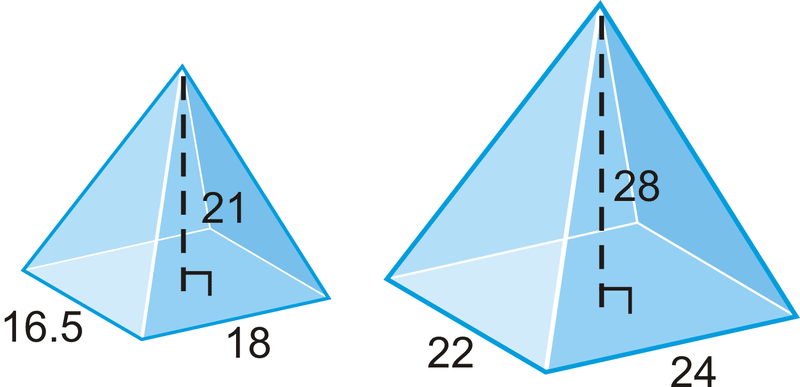
Pyramids
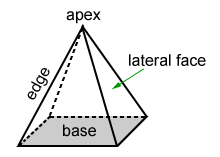
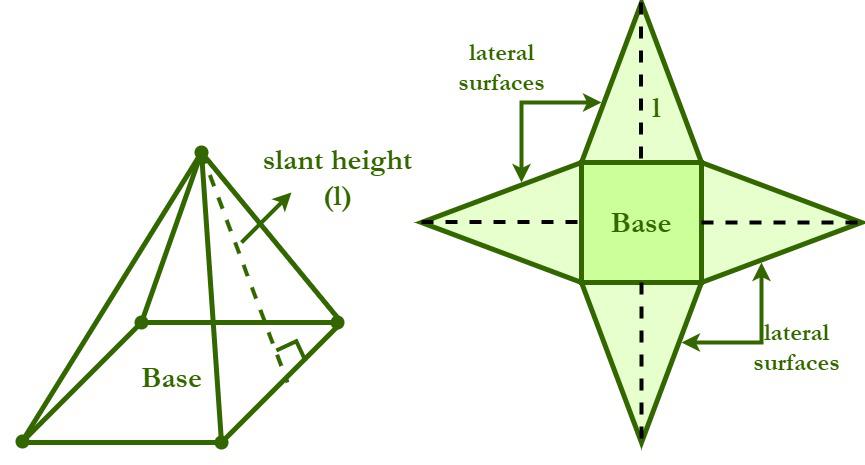
A polyhedron of which one face, called the base, is a polygon of any number of sides and the other faces are triangles having a common vertex is called a pyramid.
The triangular faces having a common vertex are called the lateral faces, their intersections are called the lateral edges, and their common vertex is called the vertex of the pyramid. The base of a pyramid may be any kind of polygon, however, usually a convex polygon is taken.
Lateral Area
The sum of the areas of the lateral faces of a pyramid is called the lateral area of the pyramid.
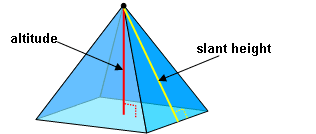
Altitude
The perpendicular distance from the vertex to the plane of the base is called the altitude of the pyramid.
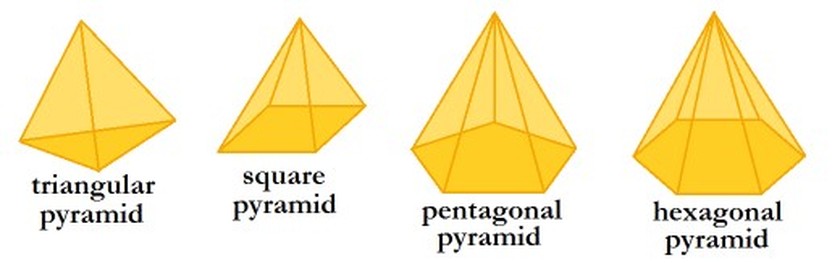
Pyramids classified as to Bases
Pyramids are said to be triangular, quadrangular, and so on, according as their bases are triangles, quadrilaterals, and so on. A triangular pyramid has four triangular faces and is called a tetrahedron. Any one of its faces may be taken as the base.
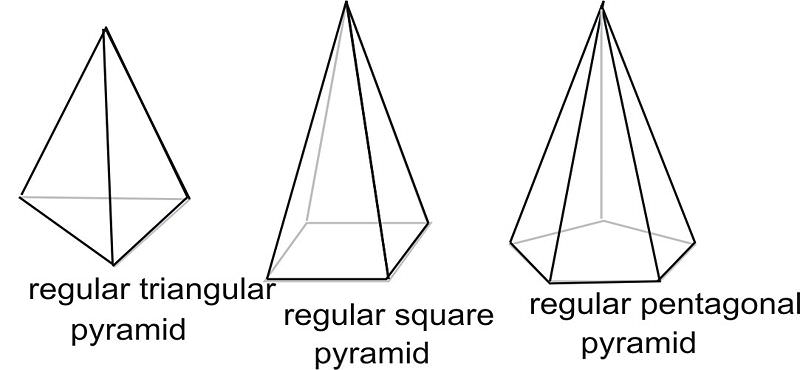
Regular Pyramid
If the base of a pyramid is a regular polygon whose center coincides with the foot of the perpendicular let fall from the vertex to the base, the pyramid is called a regular pyramid. A regular pyramid is also called a right pyramid.
Slant Height of a Regular Pyramid
The altitude of any one of the lateral faces of a regular pyramid, drawn from the vertex of the pyramid, is called the slant height. The slant height is the same whatever face is taken. Only a regular pyramid can have a slant height.
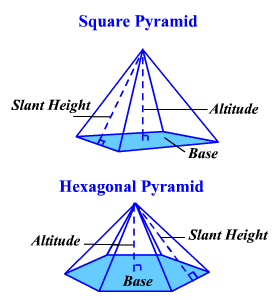
Properties of Regular Pyramids
Among the properties of regular pyramids, the following are too evident to require further proof than that referred to below:
(1) The lateral edges of a regular pyramid are equal.
(2) The lateral faces of a regular pyramid are congruent isosceles triangles.
(3) The slant height of a regular pyramid is the same for all the lateral faces.
Frustum of a Pyramid
The portion of a pyramid included between the base and a section parallel to the base is called a frustum of a pyramid. The base of the pyramid and the parallel section are called the bases of the frustum. A more general term, including frustum as a special case, is truncated pyramid, the portion of a pyramid included between the base and any section made by a plane that cuts all the lateral edges.
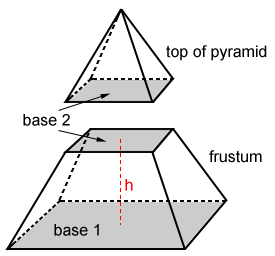
Altitude of a Frustum
The perpendicular distance between the bases is called the altitude of the frustum.
Lateral Faces of a Frustum
The portions of the lateral faces of a pyramid that lie between the bases of a frustum are called the lateral faces of the frustum. In the case of a frustum of a regular pyramid the lateral faces are congruent isosceles trapezoids. The sum of the areas of the lateral faces is called the lateral area of the frustum.
Slant Height of a Frustum
The altitude of one of the trapezoid faces of a frustum of a regular pyramid is called the slant height of the frustum.
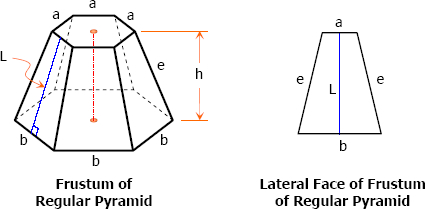
PROPOSITION XIII
The lateral area of a regular pyramid is equal to half the product of its slant height by the perimeter of its base.
Corollary
The lateral area of the frustum of a regular pyramid is equal to half the sum of the perimeters of the bases multiplied by the slant height of the frustum.
PROPOSITION XIV
If a pyramid is cut by a plane parallel to the base:
- The edges and altitude are divided proportionally.
- The section is a polygon similar to the base.
Corollary
- Any section of a pyramid parallel to the base is to the base as the square of the distance from the vertex is to the square of the altitude of the pyramid.
- If two pyramids have equal altitudes and equivalent bases, sections made by planes parallel to the bases, and at equal distances from the vertices, are equivalent.
PROPOSITION XV
Two triangular pyramids having equivalent bases and equal altitudes are equivalent.
PROPOSITION XVI
The volume of a triangular pyramid is equal to one third the product of its base by its altitude.
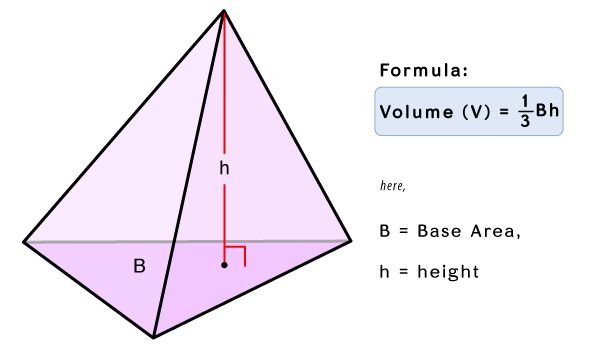
Corollary
The volume of a triangular pyramid is equal to one third the volume of a triangular prism of the same base and altitude.
PROPOSITION XVII
The volume of any pyramid is equal to one third the product of its base by its altitude.
Corollary
The volumes of two pyramids are to each other as the products of their bases and altitudes; pyramids having equivalent bases are to each other as their altitudes; pyramids having equal altitudes are to each other as their bases; pyramids having equivalent bases and equal altitudes are equivalent.
PROPOSITION XVIII
The frustum of a triangular pyramid is equivalent to the sum of three pyramids whose common altitude is the altitude of the frustum and whose bases are the lower base, the upper base, and the mean proportional between the two bases of the frustum.
Corollary
- The volume of a frustum of a triangular pyramid may be expressed as ⅓ a (b + b’ + √bb’). For we may factor by 1/3 a.
- The volume of a frustum of any pyramid is equal to the sum of the volumes of three pyramids whose common altitude is the altitude of the frustum, and whose bases are the lower base, the upper base, and the mean proportional between the bases of the frustum.
Cavalieri's Principle
An Italian mathematician of the 17th century, Bonaventura Cavalieri, formulated the following proposition.
If two solids (bounded by - no matter - plane or curved surfaces) can be positioned in such a way that, for each plane parallel to a given plane, the cross-sections of these solids by this plane are equivalent plane figures, then the volumes of these solids are equal.
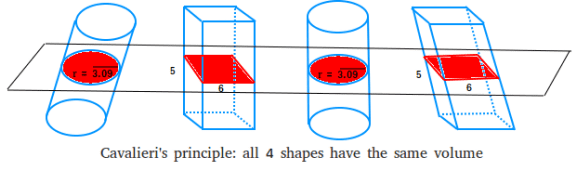
To justify Cavalieri’s principle, one needs methods that would go beyond elementary mathematics. We will merely verify the principle in several special cases. For instance, the hypotheses of Cavalieri’s principle are satisfied when two prisms (no matter – triangular or polygonal) have congruent altitudes and equivalent bases. As we already know, such prisms are equivalent. On the other hand, if such prisms are placed standing with their bases on the same plane, then every plane parallel to the bases and intersecting one of the prisms will intersect the other as well, and the cross-sections will be equivalent (since they are congruent to the respective bases which are equivalent). Therefore, Cavalieri’s principle holds true in this special case.
Cavalieri’s principle also applies to areas in plane geometry. Namely, if two figures can be positioned such that for every line parallel to a given line, its intersections with the figures have equal lengths, then the figures are equivalent. Two parallelograms or two triangles with congruent bases and congruent altitudes are good illustrations of this principle.
The following lemma establishes Cavalieri’s principle in the case of triangular pyramids.
Lemma
Triangular pyramids with congruent altitudes and equivalent bases are equivalent.
Similarity of polyhedra
Two polyhedra are called similar if they have respectively congruent polyhedral angles and respectively similar and similarly positioned faces. For example, any two cubes are similar.
Corresponding elements of similar polyhedra are called homologous. It follows from the definition, that in similar polyhedra:
- Homologous dihedral angles are congruent and similarly positioned, because the polyhedral angles are congruent;
- Homologous edges are proportional, because in each of the two similar faces the ratios between homologous edges are the same, and in each polyhedron adjacent faces have an edge in common.
PROPOSITION XIX
In a pyramid, if a cross-section parallel to the base is drawn, then it cuts off another pyramid similar to the given one.
PROPOSITION XX
Surface areas of similar polyhedra have the same ratio as the squares of homologous edges.
PROPOSITION XXI
Volumes of similar polyhedra have the same ratio as the cubes of homologous edges.
Symmetries of space figures
Central symmetry
Two geometric figures are called symmetric about a point 0 if to every point A of one of the figures there corresponds a point A’ of the other figure such that the midpoint of the segment AA’ is the point 0. The point 0 is called the center of symmetry of the figures.
Bilateral symmetry
Two geometric figures are called symmetric about a given plane P, if to every point A of one of the figures there corresponds a point A’ of the other, such that the segment AA’ is perpendicular to the plane P and is bisected by the intersection point with it. The plane P is called the plane of symmetry of the figures.

Axial Symmetry (Symmetry about a line)
Two figures are called symmetric about a line l if to every point A of one of the figures there corresponds a point A’ of the other such that the segment AA’ is perpendicular to the line l, intersects it, and is bisected by the point of intersection. The line l is called the axis of symmetry of the 2nd order.

PROPOSITION XXII
If two figures are symmetric to a given figure, one about a point, the other about a plane passing through it, then they are symmetric about the line perpendicular to the plane at this point.
Explore more
geometric principles
This post is part of our Guide to Euclidean Geometry. You can explore more or return to the index page to follow the series in sequential order.
Up Next

Solid Geometry
Welcome, to this online guide to Euclidean Geometry, produced by In2infinity, and written by Sunil…





