Welcome, to this online guide to Euclidean Geometry, produced by In2infinity, and written by Sunil Jankar. This section explores the geometric nature of the sphere.
Definition of a sphere
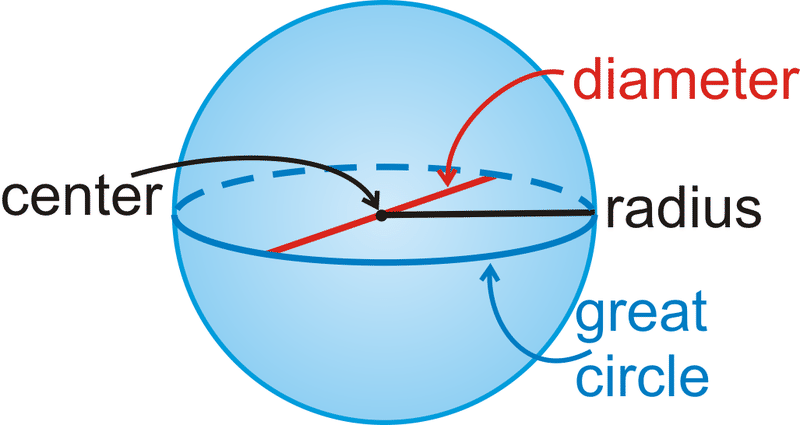
A solid bounded by a surface, all points of which are equidistant from a point within, is called a sphere. The point within, from which all points on the surface are equally distant, is called the centre. The surface is called the spherical surface, and sometimes the sphere. Half of a sphere is called a hemisphere. The terms radius and diameter are used, as in the case of a circle.
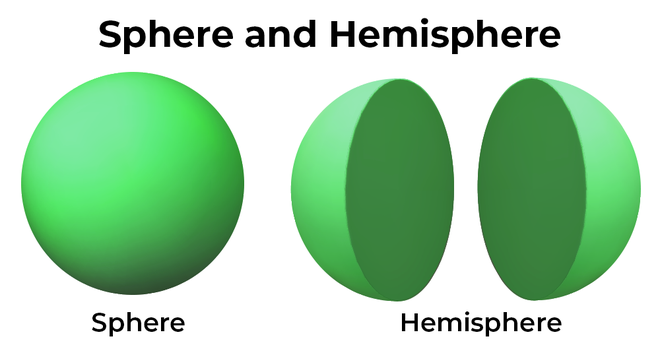
Generation of a Spherical Surface
By the definition of sphere, it appears that a spherical surface may be generated by the revolution of a semicircle about its diameter as an axis. Thus, if the semicircle A CB revolves about AB, a spherical surface is generated. It is therefore assumed that a sphere may be described with any given point as a centre and any given line as a radius.
Equality of Radii and Diameters
All radii of the same sphere are equal, and all diameters of the same sphere are equal. Equal spheres have equal radii, and spheres having equal radii are equal.
Propositions (Theorems)
PROPOSITION I
Every intersection of a spherical surface by a plane is a circle.
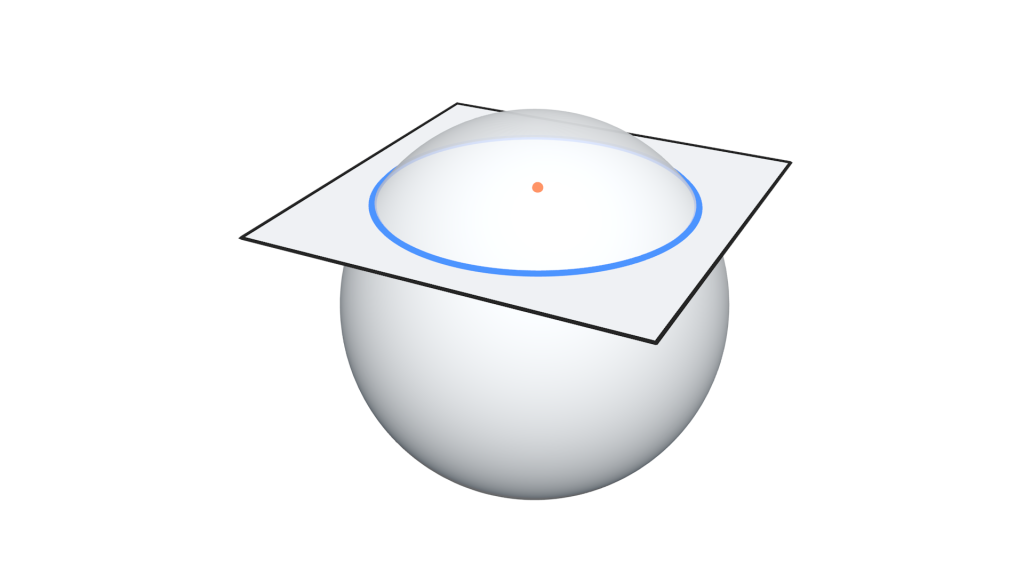
Corollary:
- The line joining the centre of a sphere surface and the centre of a circle is perpendicular to the plane of the circle.
- Circles of a sphere made by planes equidistant from the centre are equal; and of the two circles made by planes not equidistant from the centre, the one made by the plane nearer the centre is greater.
Definitions
Great Circle
The intersection of a spherical surface by a plane passing through the center is called a great circle of the sphere.
Small Circle
The intersection of a spherical surface by a plane which does not pass through the center is called a small circle of the sphere.
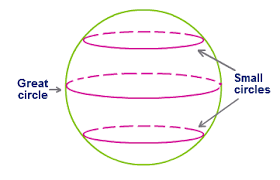
Poles of a Circle
If a diameter of a sphere is perpendicular to the plane of a circle of the sphere, the extremities are called the poles of the circle.
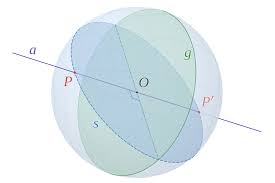
Corollary:
- Parallel circles have the same poles.
- All great circles of a sphere are equal.
- Every great circle bisects the spherical surface.
- Two great circles bisect each other.
- If the planes of two great circles are perpendicular, each circle passes through the poles of the other.
- Through two given points on the surface of a sphere, an arc of a great circle may always be drawn.
- Through three given points on the surface of a sphere, one circle and only one can be drawn.
Spherical Distance
The length of the smaller arc of the great circle joining two points on the surface of a sphere is called the spherical distance between the points, or, where no confusion is likely to arise, simply the distance.
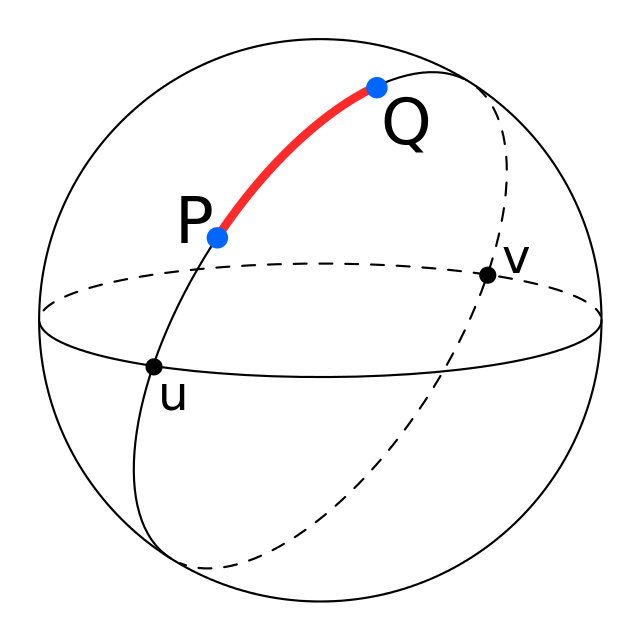
PROPOSITION II
The spherical distances of all points on a circle of a sphere from either pole of the circle are equal.
Polar Distance
The spherical distance from the nearer pole of a circle to any point on the circle is called the polar distance of the circle. The spherical distance of a great circle from either of its poles may be taken as the polar distance of the circle.
Quadrant
One fourth of a great circle is called a quadrant.
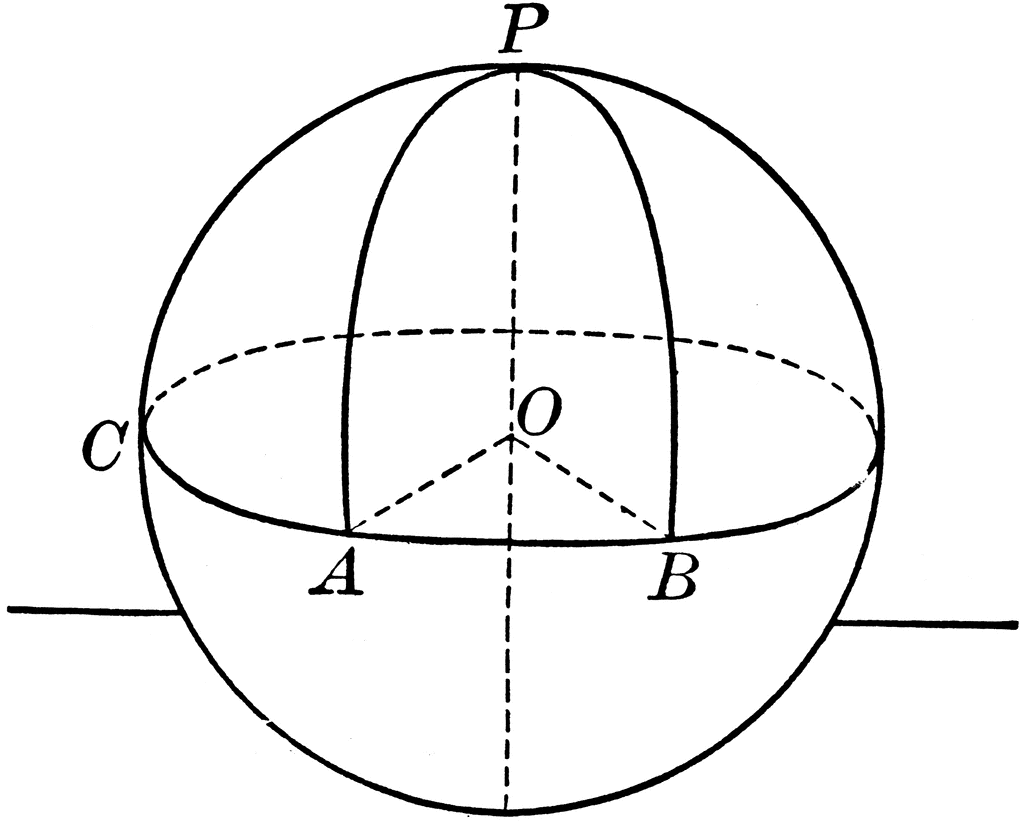
Corollary:
1.The polar distance of a great circle is a quadrant.
2. The straight lines joining points on a circle to either pole of the circle are equal.
PROPOSITION III
A point on a sphere, which is at the distance of a quadrant from each of two other points, not the extremities of a diameter, is a pole of the great circle passing through these points.
Describing Circles on a Sphere
This proposition proves that we may describe a great circle on a sphere of a given radius so that it shall pass through two given points.
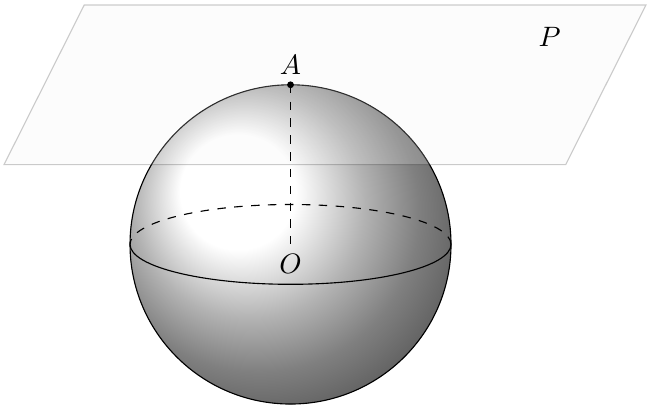
Tangent Lines and Planes
A line or plane that has one point and only one point in common with a sphere, however far produced, is said to be tangent to the sphere, and the sphere to be tangent to the line or plane.
Tangent Spheres
Two spheres whose surfaces have one point and only one point in common are said to be tangent.

PROPOSITION IV
A plane perpendicular to a radius at its extremity is tangent to the sphere.
Corollary:
A plane tangent to a sphere is perpendicular to the radius drawn to the point of contact.
Inscribed Sphere
If a sphere is tangent to all the faces of a polyhedron, it is said to be inscribed in the polyhedron, and the polyhedron to be circumscribed about the sphere.
Circumscribed Sphere
If all the vertices of a polyhedron lie on a spherical surface, the sphere is said to be circumscribed about the polyhedron, and the polyhedron to be inscribed in the sphere.
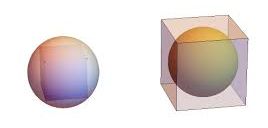
PROPOSITION V
A sphere may be inscribed in any given tetrahedron.
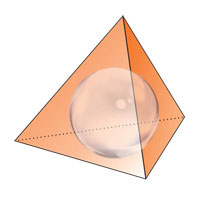
PROPOSITION VI
A sphere may be circumscribed about any given Tetrahedron.

Corollary:
Through four points not in the same plane, one spherical surface and only one can be passed. The centre of any sphere whose surface passes through the four points must be in the planes mentioned in the proof, and since there is only one point of intersection, there can be only one sphere.
PROPOSITION VII
The intersection of two spherical surfaces is a circle whose plane is perpendicular to the line which joins the centers of the spheres and whose center is in that line.
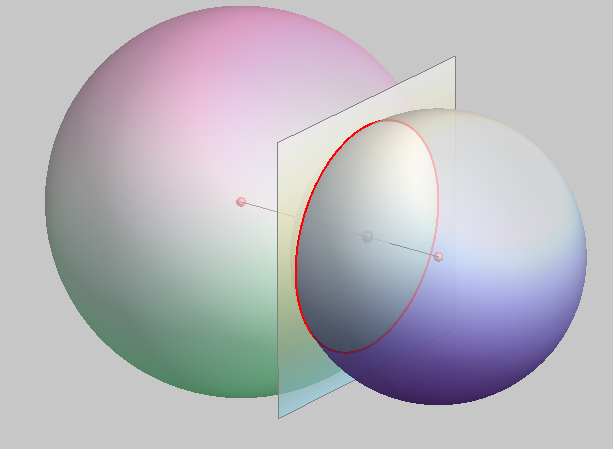
PROPOSITION VIII
A spherical angle is measured by the arc of the great circle described from its vertex as a pole and included between its sides, produced if necessary.

Corollary:
- A spherical angle has the same measure as the dihedral angle formed by the planes of the two circles.
- All arcs of great circles drawn through the pole of a given great circle are perpendicular to the given Circle.
Spherical Polygons
A portion of a spherical surface bounded by three or more arcs of great circles is called a spherical polygon. The bounding arcs are called the sides of the polygon, the angles between the sides are called the angles of the polygon, and the points of intersection of the sides are called the vertices of the polygon.
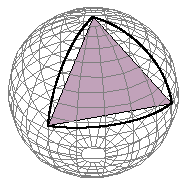
Relation of Polygons to Polyhedral Angles
The planes of the sides of a spherical polygon form a polyhedral angle whose vertex is the centre of the sphere, whose face angles are measured by the sides of the polygon, and whose dihedral angles have the same numerical measure as the angles of the polygon.
Convex Spherical Polygon
If a polyhedral angle at the centre of a sphere is convex, the corresponding spherical polygon is said to be convex.
Diagonal
An arc of a great circle joining two nonconsecutive vertices of a spherical polygon is called a diagonal.

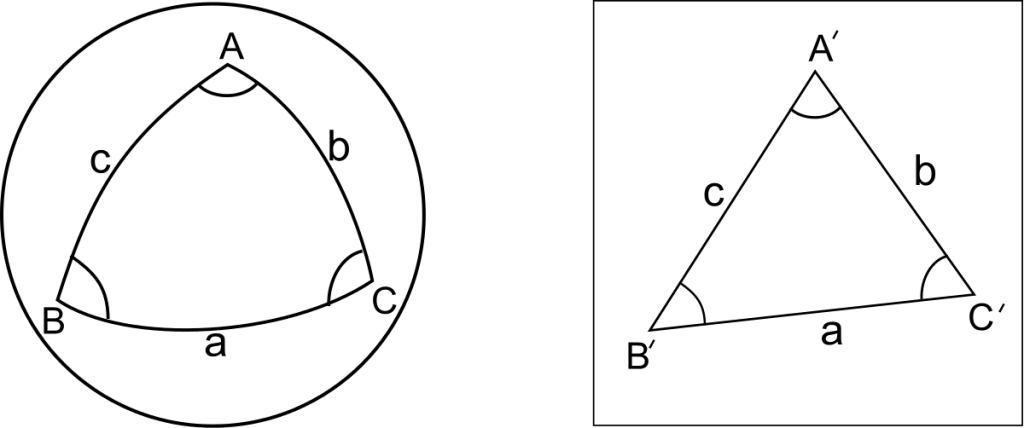
Spherical Triangle
A spherical polygon of three sides is called a spherical triangle. A spherical triangle may be right, obtuse, or acute. It may also be equilateral, isosceles, or scalene.
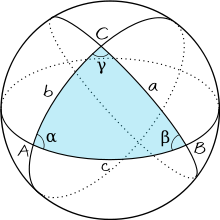
Congruent Spherical Polygons
If two spherical polygons can be applied, one to the other, so as to coincide, they are said to be congruent.

PROPOSITION IX
Each side of a spherical triangle is less than the sun of the other two sides.
PROPOSITION X
The sum of the angles of a spherical triangle is less than 360°.
Polar Triangle
If from the vertices of a spherical triangle as poles arcs of great circles are described, another spherical triangle is formed which is called the polar triangle of the first.
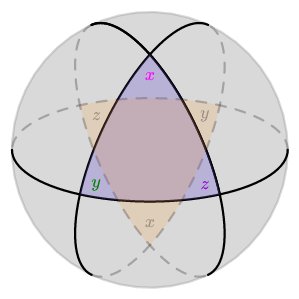
PROPOSITION XI
If one spherical triangle is the polar triangle of another, then reciprocally the second is the polar triangle of the first.
PROPOSITION XII
In two polar triangles, each angle of the one is the supplement of the opposite side in the other.
PROPOSITION XIII
The sum of the angles of a spherical triangle is greater than 180° and less than 540°
Corollary:
A spherical triangle may have two, or even three, right angles; and a spherical triangle may have two, or even three, obtuse angles.
Triangles classified as to Right Angles
A spherical triangle having two right angles is said to be bi-rectangular; one having three right angles is said to be tri-rectangular.

Symmetric Spherical Triangles
If through the centre of a sphere three diameters AA’, BB’, CC’ are drawn, and the points A, B, C are joined by arcs of great circles, and also the points A’, B’, C’, the two spherical triangles ABC and A’B’C’ are called symmetric spherical triangles. In the same way, we may form two symmetric polygons of any number of sides. Having thus formed the symmetric polygons, we may place them in any position we choose upon the surface of the sphere.
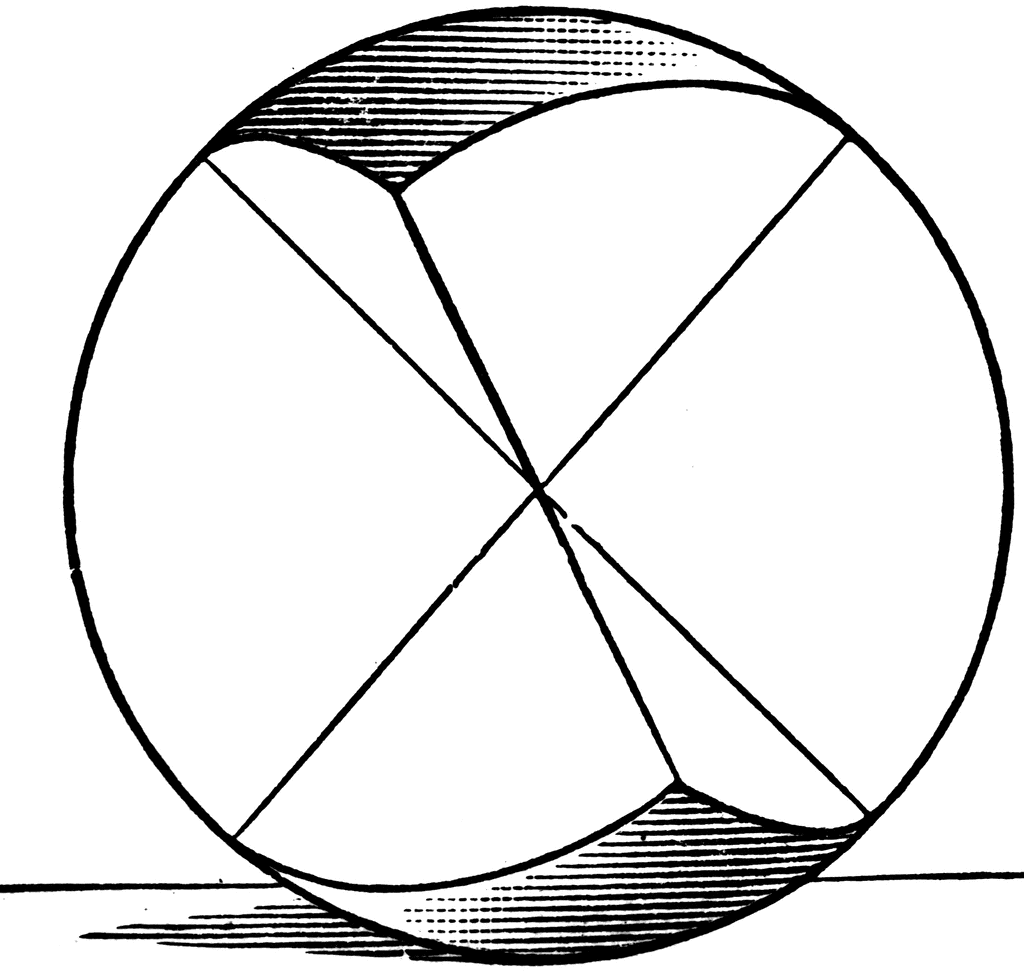
Relation of Symmetric Triangles
Two symmetric triangles are mutually equilateral and mutually equiangular; yet in general they are not congruent, for they cannot be made to coincide by superposition.
Symmetric Isosceles Triangles
If, however, we have two symmetric triangles ABC and A’B’C’ such that AB=AC, and A’B’ =A’C’, that is, if the two symmetric triangles are isosceles, then because AB, AC, A’B’, A’C’ are all equal and the angles A and A’ are equal, being originally formed by vertical dihedral angles, the B B’ two triangles can be made to coincide. Therefore, If two symmetric spherical triangles are isosceles, they are superimposable and therefore are congruent.
PROPOSITION XIV
Two symmetric spherical triangles are equivalent.
PROPOSITION XV
Two triangles on the same sphere or on equal spheres are either congruent or symmetric if two sides and the included angle of the one are respectively equal to the corresponding parts of the other.
PROPOSITION XVI
Two triangles on the same sphere or on equal spheres are either congruent or symmetric if two angles and the included side of the one are respectively equal to the corresponding parts of the other.
PROPOSITION XVII
Two mutually equilateral triangles on the same sphere or on equal spheres are mutually equiangular, and are either congruent or symmetric.
PROPOSITION XVIII
Two mutually equiangular triangles on the same sphere or on equal spheres are mutually equilateral, and are either congruent or symmetric
PROPOSITION XIX
In an isosceles spherical triangle, the angles opposite the equal sides are equal
PROPOSITION XX
If two angles of a spherical triangle are equal, the sides opposite these angles are equal and the triangle is isosceles.
PROPOSITION XXI
If two angles of a spherical triangle are unequal, the sides opposite these angles are unequal, and the side opposite the greater angle is the greater; and if two sides are unequal, the angles opposite these sides are unequal, and the angle opposite the greater side is the greater.
PROPOSITION XXII
The shortest line that can be drawn on the surface of a sphere between two points is the arc of a great circle joining the two points, not greater than a semicircle.
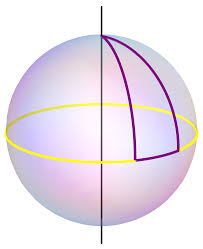
Zone and Lume
Zone
A portion of a spherical surface included between two parallel planes is called a zone. The circles made by the planes are called the bases of the zone, and the distance between the planes is called the altitude of the zone. If one of the planes is tangent to the sphere and the other plane cuts the sphere, the zone is called a zone of one base. If both planes are tangent to the sphere, the zone is a complete spherical surface.
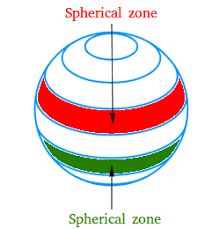
Generation of a Zone
If a great circle revolves about its diameter as an axis, any arc of the circle generates a zone.
Lune
A portion of a spherical surface bounded by the halves of two great circles is called a lune. A lune is evidently generated by the partial or complete revolution of half of a great circle about its diameter as an axis.

Angle of a Lune
The angle between the semicircles bounding a lune is called the angle of the Lune. A lune is usually taken as having an angle less than a straight angle. This is not necessary, for we may consider a hemispherical surface as a lune with an angle of 180°. We may also conceive of lunes with angles greater than a straight angle, and we may even think of an entire spherical surface as a lune whose angle is 360°.
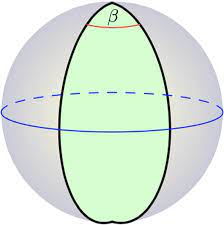
PROPOSITION XXIII
The area of the surface generated by a straight line revolving about an axis in its plane is equal to the product of the projection of the line on the axis by the circle whose radius is a perpendicular erected at the mid-point of the line and terminated by the axis.
PROPOSITION XXIV
The area of the surface of a sphere is equal to the product of the diameter by the circumference of a great circle.
Corollary
- The area of the surface of a sphere is equivalent to the area of four great circles, or to 4π × r².
- The areas of the surfaces of two spheres are to each other as the squares on their radii, or as the squares on their diameters.
- The area of a zone is equal to the product of the altitude by the circumference of a great circle.
- The area of a zone of one base is equivalent to the area of a circle whose radius is the chord of the generating arc.
Spherical Excess of a Triangle
The excess of the sum of the angles of a spherical triangle over 1800 is called the spherical excess of the triangle.
PROPOSITION XXV
The area of a lune is to the area of the surface of the sphere as the angle of the lune is to four right angles
PROPOSITION XXVI
A spherical triangle is equivalent to a lune whose angle is half the spherical excess of the triangle.
Corollary:
If two great-circle arcs intersect within a great circle, the sum of the two opposite spherical triangles which they form with the great circle is equivalent to a lune whose angle is the angle between the arcs.
PROPOSITION XXVII
A spherical polygon is equivalent to a lune whose angle is half the spherical excess of the polygon.
Segments of a Sphere
Spherical Pyramid
A portion of a sphere bounded by a spherical polygon and the planes of its sides is called a spherical pyramid. The center of the sphere is called the vertex of the spherical pyramid, and the spherical polygon is called the base.
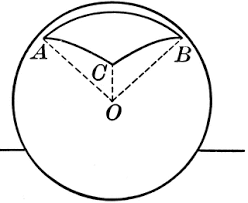
Spherical Sector
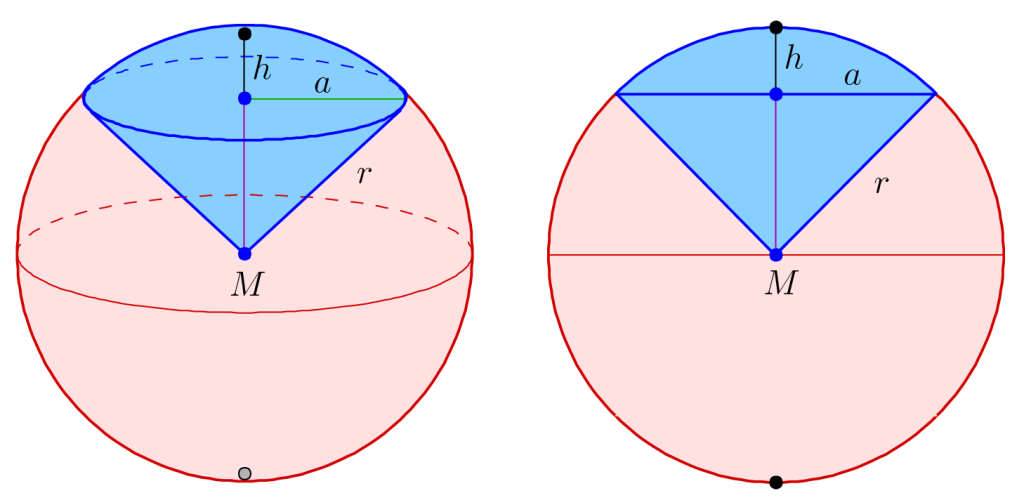
A portion of a sphere generated by the revolution of a circular sector about any diameter of the circle of which the sector is a part is called a spherical sector.
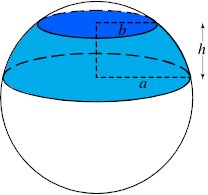
Spherical Segment
A portion of a sphere contained between two parallel planes is called a spherical segment. The sections of the sphere made by the parallel planes are called the bases of the spherical segment, and the distance between these bases is called the altitude of the spherical segment. If one of the parallel planes is tangent to the sphere, the segment is called a spherical segment of one base. A spherical segment of one base may be generated by the revolution of a circular segment about the diameter perpendicular to its base.
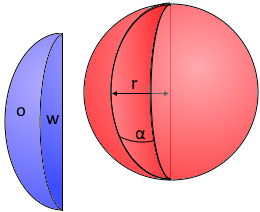
Spherical Wedge
A portion of a sphere bounded by a lune and the planes of two great circles is called a spherical wedge.
PROPOSITION XXVIII
The volume of a sphere is equal to the product of the area of its surface by one third of its radius.
Corollary:
- The volume of a sphere of radius r and diameter d is equal to 4/3 (π×r³) or ⅙ (π×d³).
- The volumes of two spheres are to each other as the cubes of their radii.
- The volume of a spherical sector is equal to one third the product of the area of the zone which forms its base multiplied by the radius of the sphere.
Explore more
geometric principles
This post is part of our Guide to Euclidean Geometry. You can explore more or return to the index page to follow the series in sequential order.
Up Next
Polyhedra - II (Cylinders and Cones)
Welcome, to this online guide to Euclidean Geometry, produced by In2infinity, and written by Sunil…







