What is a Solid?
Solid geometry deals with objects which require an additional dimension called height (or depth) in order to describe them, in addition to length and breadth used to define objects in the previous sections on plane geometry. Common examples of such objects would include ball shape (sphere) and boxes (rectangular or cubical) among various others. These objects are discussed in great length in other sections.
The most basic elements in the discussion of plane geometry were lines and angles, in the same manner the most basic elements we need to understand before we start our exposition of solid geometry would be planes and solid angles. The following article would deal with these basic elements of solid geometry. We start with defining what exactly these elements are, and then later deal with how they behave in a three-dimensional space and what properties they exhibit.
Classical Euclidean Definitions
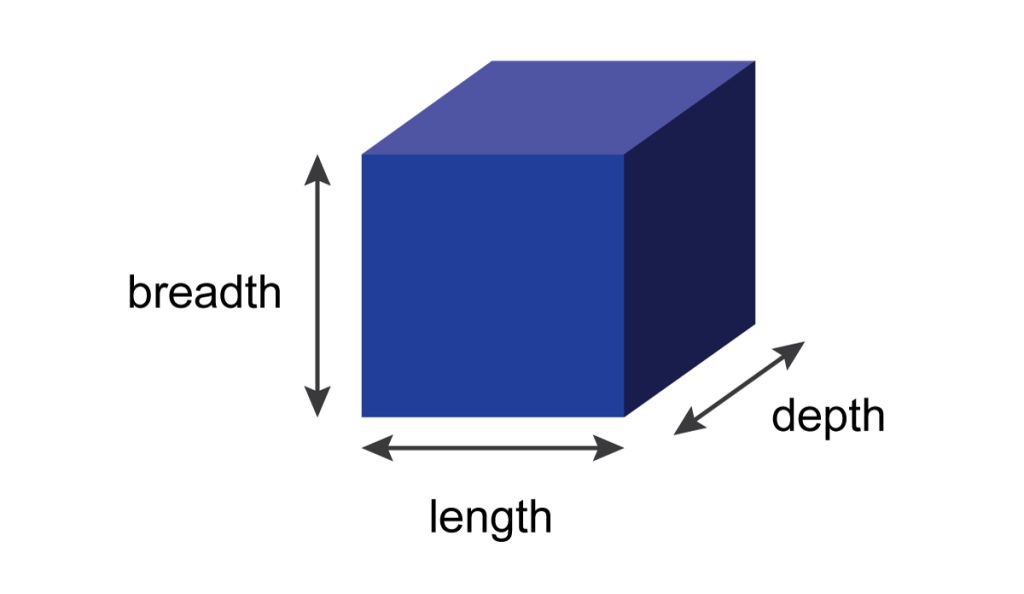
- A solid is that which has length, breadth, and depth.
- A face of a solid is a surface.
- A surface such that a straight line joining any two of its points lies wholly on the surface is called a plane.
- A straight line is at right angles to a plane when it makes right angles with all the straight lines which meet it and are in the plane.
- A plane is at right angles to a plane when the straight lines drawn in one of the planes at right angles to the intersection of the planes are at right angles to the remaining plane.
- The inclination of a straight line to a plane is, assuming a perpendicular drawn from the end of the straight line which is elevated above the plane to the plane, and a straight line joined from the point thus arising to the end of the straight line which is in the plane, the angle contained by the straight line so drawn and the straight line standing up.
- The inclination of a plane to a plane is the acute angle contained by the straight lines drawn at right angles to the intersection at the same point, one in each of the planes.
- A plane is said to be similarly inclined to a plane as another is to another when the said angles of the inclinations equal one another.
- Parallel planes are those which do not meet.
- A solid angle is the inclination constituted by more than two lines which meet one another and are not in the same surface, towards all the lines, that is, a solid angle is that which is contained by more than two plane angles which are not in the same plane and are constructed to one point.
More terms and definitions will be discussed in the following sections as and when and in the context they arise.
LINES AND PLANES
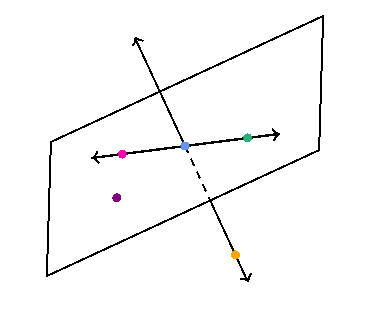
Determining a Plane
A plane is said to be determined by certain lines or points if it contains the given lines or points, and no other plane can contain them. When we suppose a plane to be drawn to include given points or lines, we are said to pass the plane through these points or lines. When a straight line is drawn from an external point to a plane, its point of contact with the plane is called its foot.
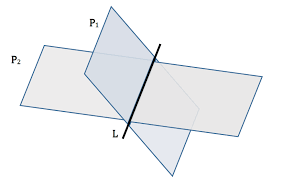
Intersection of Planes
The line that contains all the points common to two planes is called their intersection.
Postulate of Planes
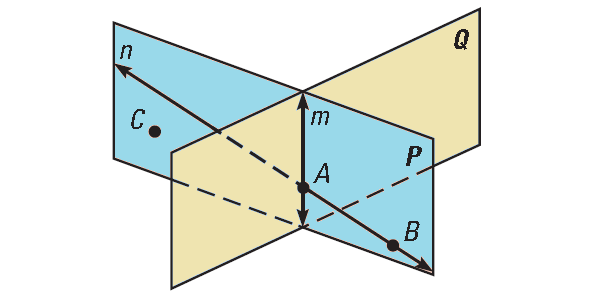
Corresponding to the postulate that one straight line, and only one, can be drawn through two given points, the following postulate is assumed for planes:
One plane, and only one, can be passed through two given intersecting straight lines.
Corollary:
- A straight line and a point not in the line determine a plane.
- Three points not in a straight line determine a plane. For by joining any one of them with the other two we have two intersecting lines
- Two parallel lines determine a plane.
PREPOSITIONS (THEOREMS)
PROPOSITION I
If two planes cut each other, their intersection is a straight line.
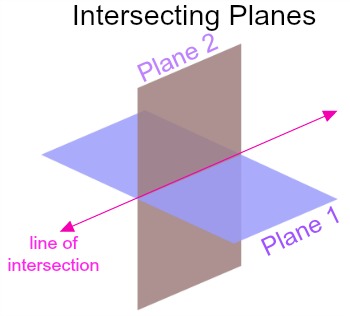
Intersection of Planes
The line that contains all the points common to two planes is called their intersection.
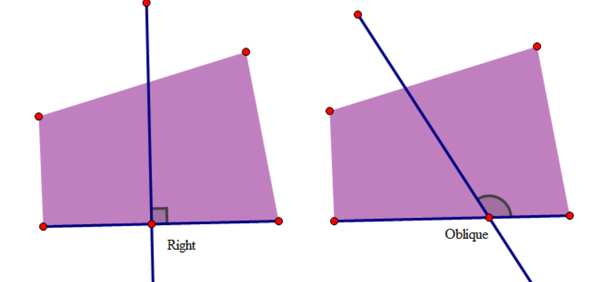
Perpendicular to a Plane
If a straight line drawn to a plane is perpendicular to every straight line that passes through its foot and lies in the plane, it is said to be perpendicular to the plane. When a line is perpendicular to a plane, the plane is also said to be perpendicular to the line.
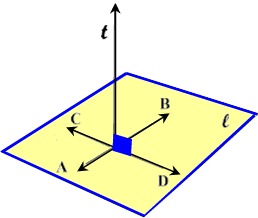
PROPOSITION II
If a line is perpendicular to each of two other lines at their point of intersection, it is perpendicular to the plane of the two lines.
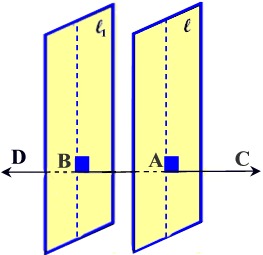
PROPOSITION III
All the perpendiculars that can be drawn to a given line at a given point lie in a plane which is perpendicular to the given line at the given point.
Corollary:
- Through a given point in a given line one plane, and only one, can be passed perpendicular to the line.
- Through a given external point one plane, and only one, can be passed perpendicular to a given line.
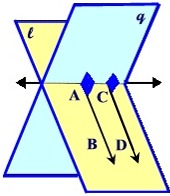
Oblique Line
A line that meets a plane but is not perpendicular to it is said to be oblique to the plane.
PROPOSITION IV
Through a given point in a plane, there can be drawn one line perpendicular to the plane, and only one.
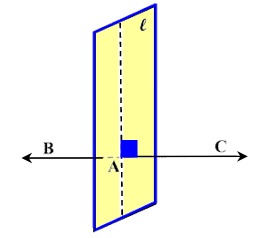
PROPOSITION V
Through a given external point there can be drawn one line perpendicular to a given plane, and only one.
Corollary:
The perpendicular is the shortest line from a point to a plane.
PROPOSITION VI
Oblique lines drawn from a point to a plane, meeting the plane at equal distances from the foot of the perpendicular, are equal; and of two oblique lines, meeting the plane at unequal distances from the foot of the perpendicular, the more remote is the greater.
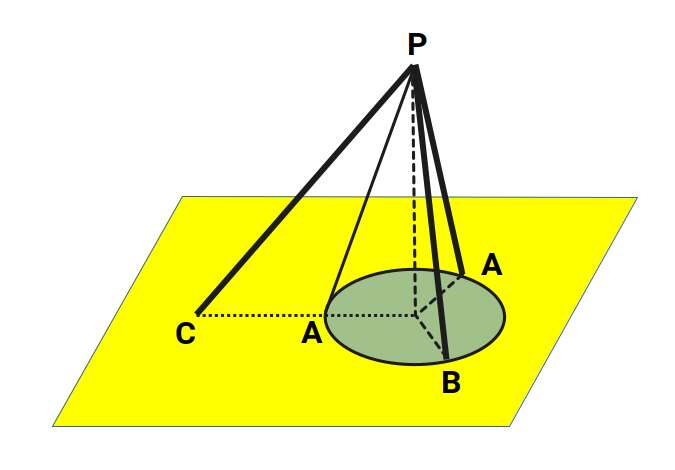
Corollary:
- Equal oblique lines drawn from a point to a plane meet the plane at equal distances from the foot of the perpendicular; and of two unequal oblique lines, the greater meets the plane at the greater distance from the foot of the Perpendicular.
- The locus of a point equidistant from all points on a circle is a line through the centre, perpendicular to the plane of the circle.
- The locus of a point equidistant from the vertices of a triangle is a line through the centre of the circumscribed circle, perpendicular to the plane of the triangle.
- The locus of a point equidistant from two given points is the plane perpendicular to the line joining them, at its mid-point.
PROPOSITION VII
Two lines perpendicular to the same plane are Parallel.
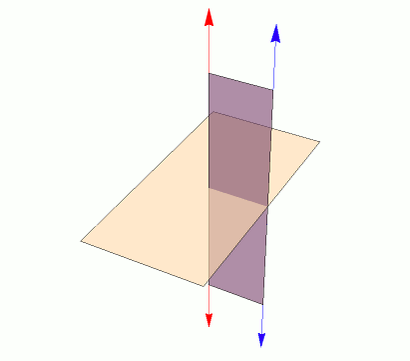
Corollary:
- If one of two parallel lines is perpendicular to a plane, the other is also perpendicular to the plane.
- If two lines are parallel to a third line, they are parallel to each other.
Line and Plane Parallel
If a line and plane cannot meet, however far produced, they are said to be parallel.
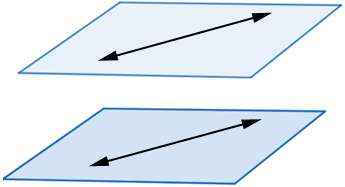
PROPOSITION VIII
If two lines are parallel, every plane containing one of the lines, and only one, is parallel to the other line.
Corollary:
- Through either of two lines not in the same plane one plane, and only one, can be passed parallel to the other.
- Through a given point one plane, and only one, can be passed parallel to any two given lines in space.
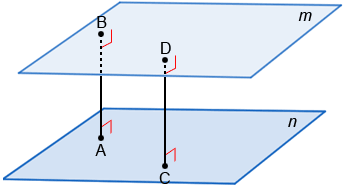
Parallel Planes
Two planes which cannot meet, however far produced, are said to be parallel.
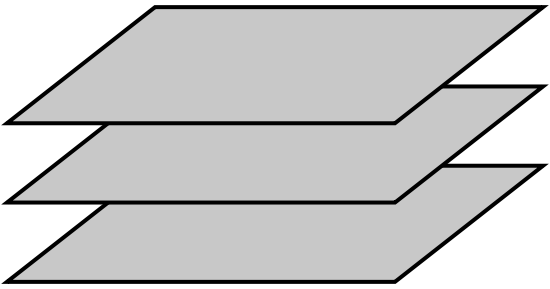
PROPOSITION IX
Two planes perpendicular to the same line are parallel.
PROPOSITION X
The intersections of two parallel planes by a third plane are parallel lines.
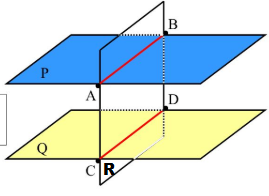
Corollary:
- Parallel lines included between parallel planes are equal.
- Two parallel planes are everywhere equidistant from each other.
PROPOSITION XI
A line perpendicular to one of two parallel planes is also perpendicular to the other.
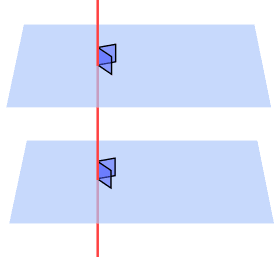
Corollary:
- Through a given point one plane, and only one, can be passed parallel to a given plane.
- The locus of a point equidistant from two parallel planes is a plane perpendicular to a line which is perpendicular to the planes and which bisects the segment cut off by them.
- The locus of a point equidistant from two parallel lines is a plane perpendicular to a line which is perpendicular to the given lines and which bisects the segment cut off by them.
PROPOSITION XII
If two intersecting lines are each parallel to a plane, the plane of these lines is parallel to that plane.
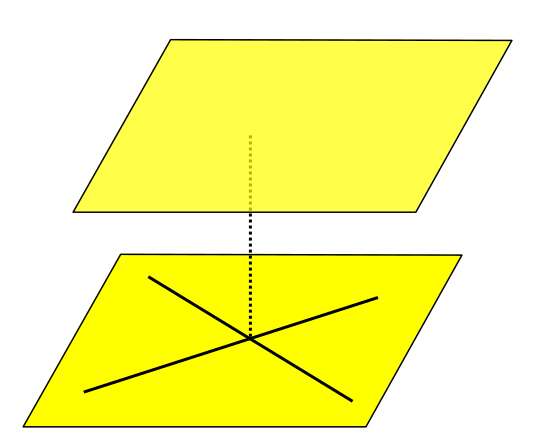
PROPOSITION XIII
If two angles not in the same plane have their sides respectively parallel and lying on the same side of the straight line joining their vertices, the angles are equal, and their planes are parallel.
PROPOSITION XIV
If two lines are cut by three parallel planes, their corresponding segments are proportional.
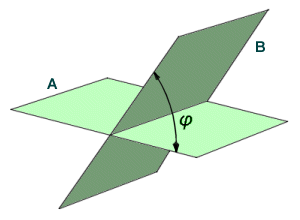
DIHEDRAL ANGLES
The opening between two intersecting planes is called a dihedral angle.
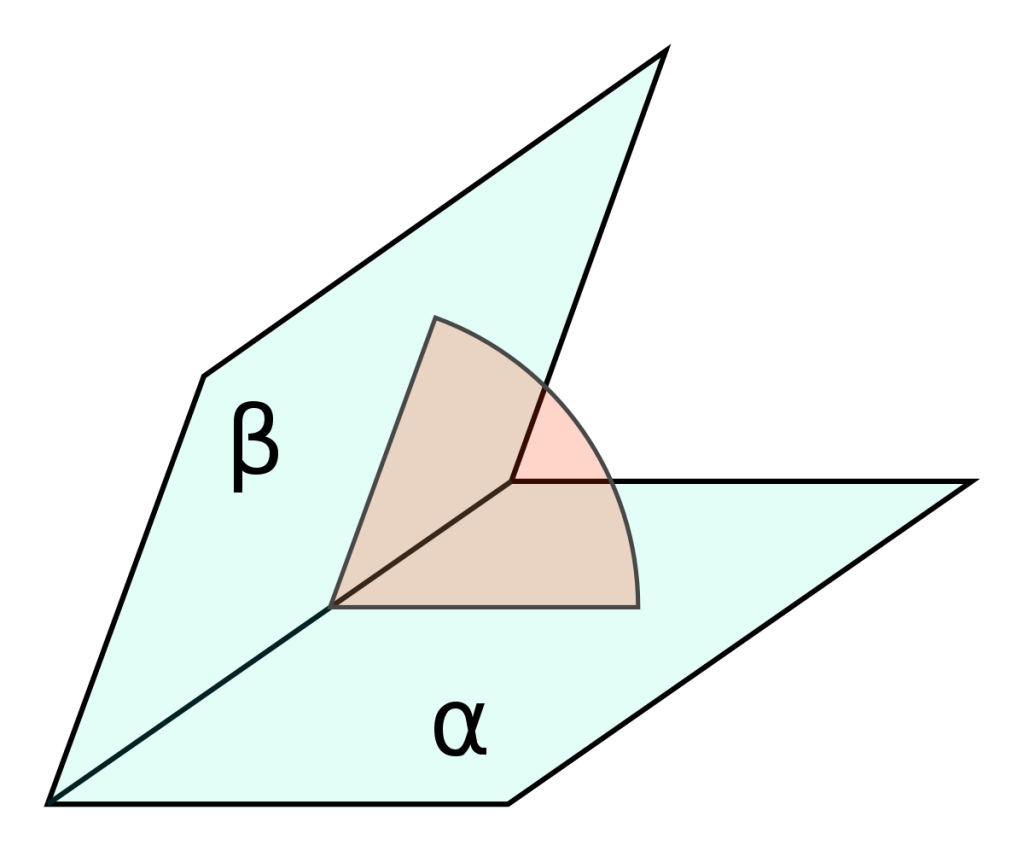
Size of a Dihedral Angle
The size of a dihedral angle depends upon the amount of turning necessary to bring one face into the position of the other.
Adjacent Dihedral Angles
If two dihedral angles have a common edge, and a common face between them, they are said to be adjacent dihedral angles.
Right Dihedral Angle
If one plane meets another plane and makes the adjacent dihedral angles equal, each of these angles is called a right dihedral angle. Dihedral angles are said to be straight, acute, obtuse, reflex, complementary, supplementary, conjugate, and vertical, under conditions similar to those obtained with plane angles. There is little occasion, however, to use any of these terms in connection with dihedral angles.
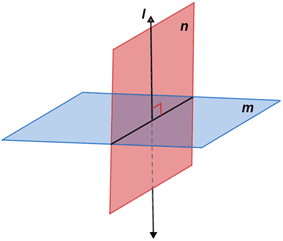
Perpendicular Planes
If two planes intersect and form a right dihedral angle, each of the planes is said to be perpendicular to the other plane.
Plane Angle of a Dihedral Angle
The plane angle formed by two straight lines, one in each plane, perpendicular to the edge at the same point, is called the plane angle of the dihedral angle.
Corollary:
The plane angle of a dihedral angle has the same magnitude from whatever point in the edge the perpendiculars are drawn.
Relation of Dihedral Angles to Plane Angles
It is apparent that the demonstrations of many properties of dihedral angles are identically the same as the demonstrations of analogous properties of plane angles. A few of the more important propositions will be proved, but the following may be assumed or may be taken as exercises:
- If a plane meets another plane, it forms with it two adjacent dihedral angles whose sum is equal to two right dihedral angles.
- If the sum of two adjacent dihedral angles is equal to two right dihedral angles, their exterior faces are in the same plane.
- If two planes intersect each other, their vertical dihedral angles are equal.
- If a plane intersects two parallel planes, the alternate-interior dihedral angles are equal; the exterior-interior dihedral angles are equal; and the two interior dihedral angles on the same side of the transverse plane are supplementary.
- When two planes are cut by a third plane, if the alternate-interior dihedral angles are equal, or the exterior-interior dihedral angles are equal, and the edges of the dihedral angles thus formed are parallel, the two planes are parallel.
- Two dihedral angles whose faces are parallel each to each are either equal or supplementary.
- Two dihedral angles whose faces are perpendicular each to each, and whose edges are parallel, are either equal or supplementary.
PROPOSITION XV
Two dihedral angles are equal if their plane angles are equal.
PROPOSITION XVI
Two dihedral angles have the same ratio as their plane angles.
Corollary:
The plane angle of a dihedral angle may be taken as the measure of the dihedral angle.
PROPOSITION XVII
If two planes are perpendicular to each other, a line drawn in one of them perpendicular to their intersection is perpendicular to the other.
Corollary:
- If two planes are perpendicular to each other, a perpendicular to one of them at any point of their intersection will lie in the other.
- If two planes are perpendicular to each other, a perpendicular to the first from any point in the second will lie in the second.
PROPOSITION XVIII
If a line is perpendicular to a plane, every plane passed through this line is perpendicular to the plane.
PROPOSITION XIX
If two intersecting planes are each perpendicular to a third plane, their intersection is also perpendicular to that plane.
PROPOSITION XX
The locus of a point equidistant from the faces of a dihedral angle is the plane bisecting the angle.
PROPOSITION XXI
Through a given line not perpendicular to a given plane, one plane and only one can be passed perpendicular to the plane.
PROPOSITION XXII
The projection of a straight line not perpendicular to a plane, upon that plane, is a straight line.
Corollary:
The projection of a straight line perpendicular to a plane, upon that plane, is a point.
Inclination of a Line
The angle which a line makes with its projection on a plane is considered as the angle which it makes with the plane, and is called the inclination of the line to the plane.
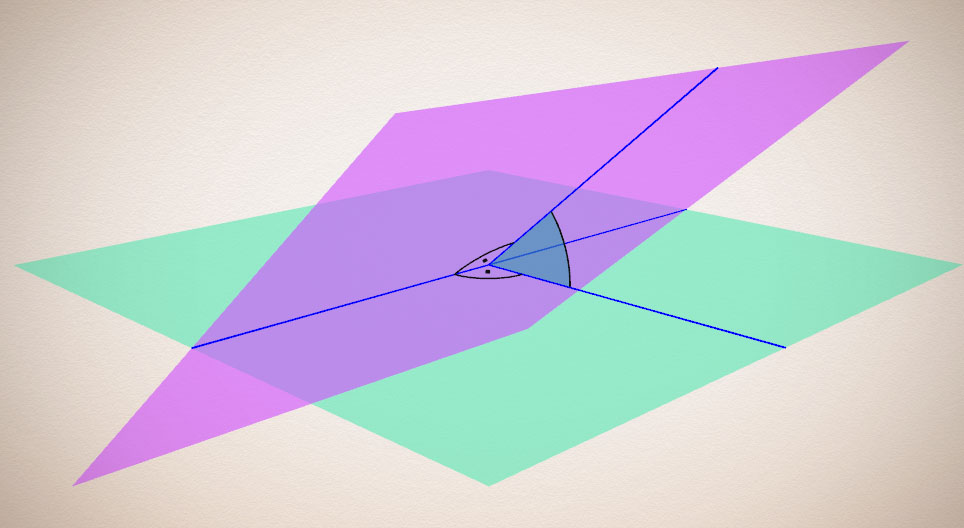
PROPOSITION XXIII
The acute angle which a line makes with its projection upon a plane is the least angle which it makes with any line of the plane.
PROPOSITION XXIV
Between two lines not in the same plane there can be one common perpendicular, and only one.
Corollary:
The common perpendicular between two lines not in the same plane is the shortest line joining them.
Polyhedral Angle
The opening of three or more planes which meet at a common point is called a polyhedral angle.
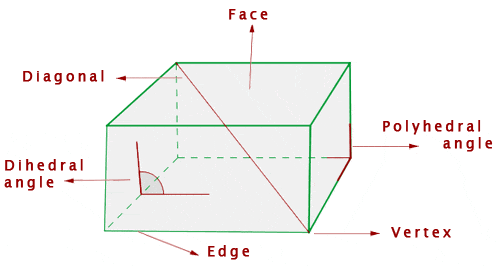
Size of a Polyhedral Angle
The size of a polyhedral angle depends upon the relative position of its faces, and not upon their extension.
Convex and Concave Polyhedral Angles
A polyhedral angle is said to be convex or concave according as a section made by a plane that cuts all its edges at other points than the vertex is a convex or concave polygon. Only convex polyhedral angles are considered in this work.
Classes of Polyhedral Angles
A polyhedral angle is called a trihedral angle if it has three faces, a tetrahedral angle if it has four faces, and so on.
Equal Polyhedral Angles
If the corresponding parts of two polyhedral angles are equal and are arranged in the same order, the polyhedral angles are said to be equal.
PROPOSITION XXV
The sum of any two face angles of a trihedral angle is greater than the third face angle.
PROPOSITION XXVI
The sum of the face angles of any convex polyhedral angle is less than four right angles.
Symmetric Polyhedral Angles
If the faces of a polyhedral angle V-ABCD are produced through the vertex V, another polyhedral angle S-A’B’C’D’ is formed, symmetric with respect to S-ABCD.
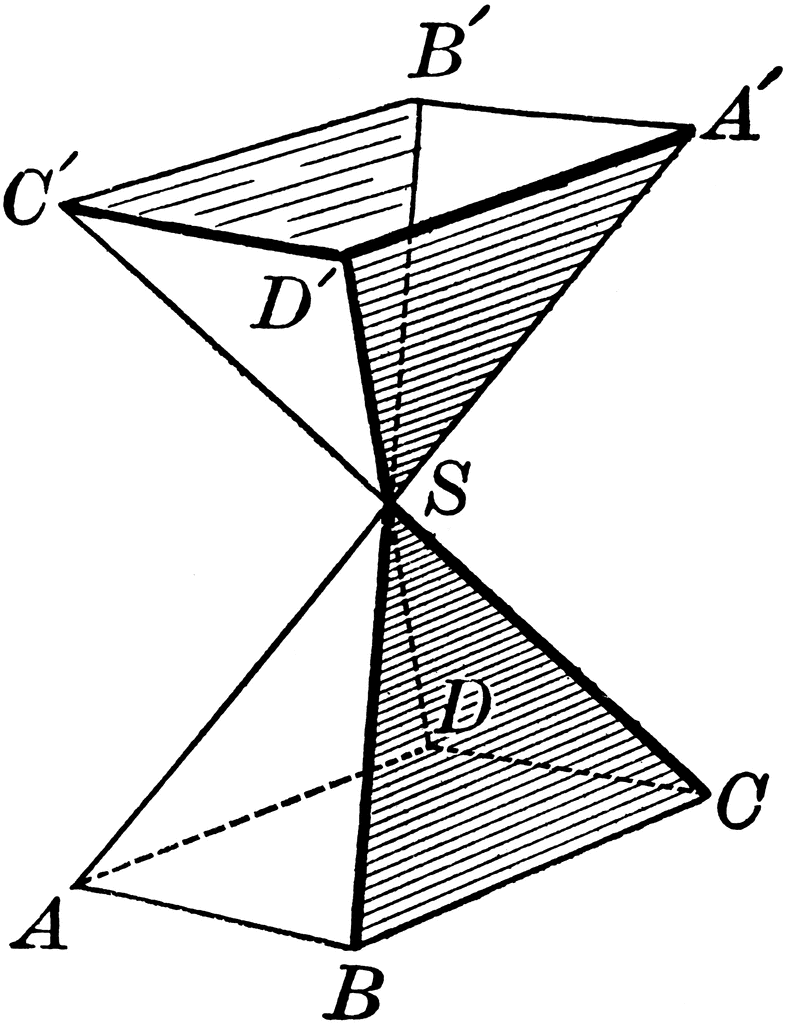
Symmetric Polyhedral Angles not Superimposable
In general, two symmetric polyhedral angles are not superimposable.
PROPOSITION XXVII
Two trihedral angles are equal or symmetric when the three face angles of the one are equal respectively to the three face angles of the other.
Corollary:
If two trihedral angles have the three face angles of the one equal respectively to the three face angles of the other, then the dihedral angles of the one are equal respectively to the dihedral angles of the other.
Explore more
geometric principles
This post is part of our Guide to Euclidean Geometry. You can explore more or return to the index page to follow the series in sequential order.
Up Next
Lines & Planes
Welcome, to this online guide to Euclidean Geometry, produced by In2infinity, and written by Sunil…
