Create the 5 Platonic Solids
What are Polyhedra?
Polyhedra are three-dimensional shapes made up of flat surfaces called faces, edges, and vertices. There are many types of polyhedra that exist, but they can be broadly classified into three main categories: regular polyhedra, semi-regular polyhedra, and irregular polyhedra. In this post, we will give an overview of the regular and semi-regular Polyhedra.
Regular Polyhedra
Regular polyhedra are polyhedra in which all the faces are congruent (identical in form) regular polygons, and the same number of faces meet at each vertex.
The 5 Platonic Solids
The regular polyhedrons are the tetrahedron, the hexahedron, or cube, the octahedron, the dodecahedron, and the icosahedron. Since these solids were extensively studied by the pupils of Plato, the great Greek philosopher, they are often called the Platonic Bodies or Platonic Solids.
Determining the number of regular Polyhedra
Greek Philosopher Euclid first observed that in a regular convex polyhedron, the angles that come together at a given vertex must add up to less than 360 degrees. This means that, at least three faces must meet at each vertex.
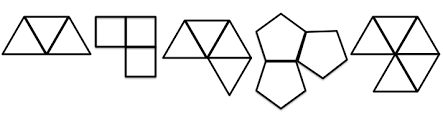
Triangular-faced Polyhedra
For a regular polyhedron with triangular faces, there are only three possibilities as it is based on a 60° angle: three (180°), four (240°), or five triangles (300°) at each vertex. Six triangles (360°) will create a hexagon on a flat plane, which would prevent to fold the object into 3D space. This defines the only possible triangular-faced regular polyhedra to be the tetrahedron, octahedron and icosahedron.
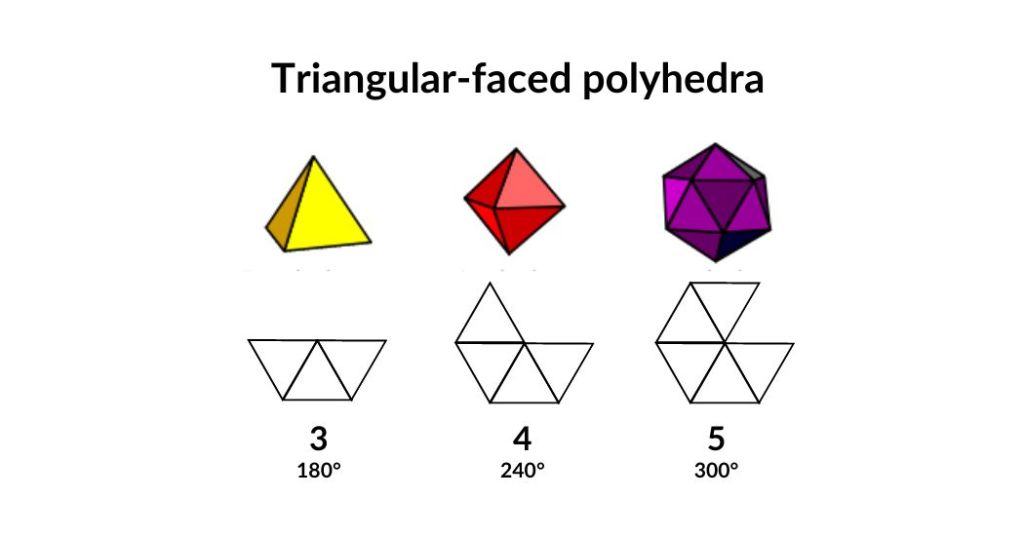
square-faced Polyhedron
Since each angle of a square is 90°, a convex polyhedral angle may be formed by combining three squares (270°). The sum of four such angles is 360°, and therefore is greater than the sum of the face angles of a convex polyhedral angle. Hence, only one regular convex polyhedron is possible with squares. This is the hexahedron, or more commonly referred to as cube.
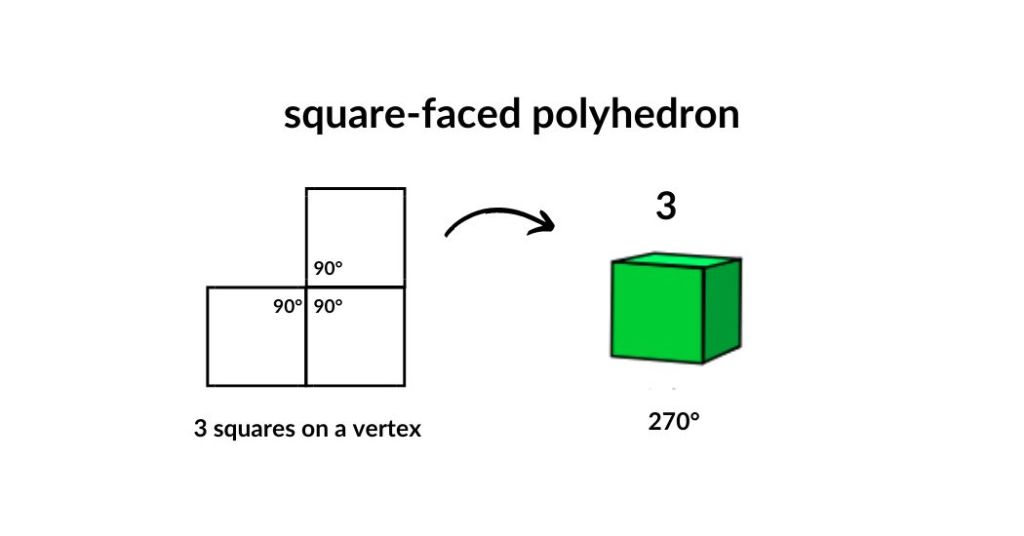
Pentagonal-faced Polyhedron
Since each angle of a regular pentagon is 108°, a convex polyhedral angle may be formed by combining three regular pentagons. The sum of four such angles is 432°, and therefore is greater than the sum of the face angles of a convex polyhedral angle. Hence, only one regular convex polyhedron is possible with regular pentagons. This is the dodecahedron.
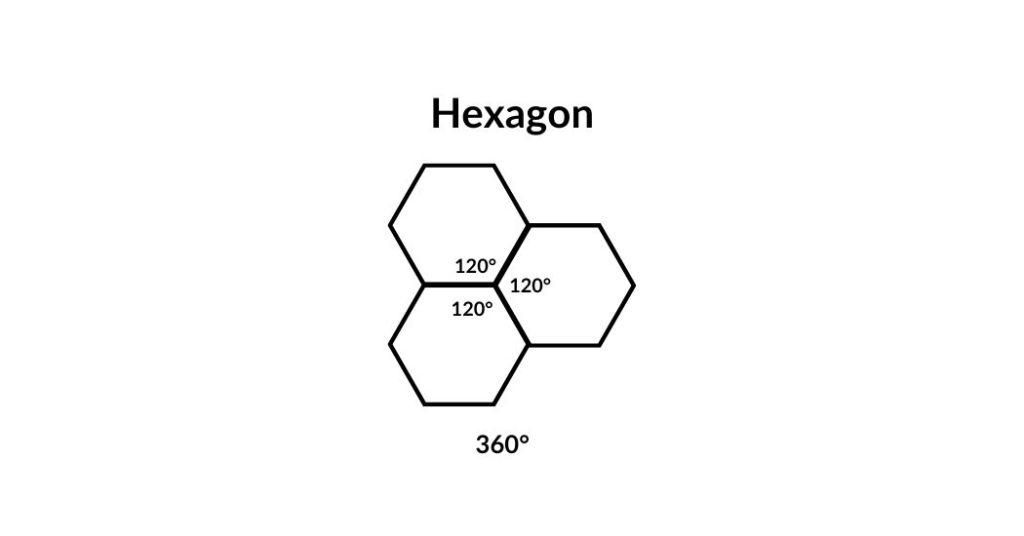
Only 5 possible Regular Polyhedra
The sum of three angles of a regular hexagon is 360°, of a regular heptagon is greater than 360°, and so on. Hence only five regular convex polyhedrons are possible.
Semi-Regular Polyhedra
In the 4th century, Greek mathematician, Pappus, first described a set of semi-regular polyhedra known as the Archimedean solids as he attributed them to Archimedes. These are ‘facially’ regular, i.e. every face is a regular polygon, though the faces are not all the same kind. Every vertex, however, is to be congruent to every other vertex, i.e. the faces must be arranged in the same order around each vertex. These are created from the regular polygons, the triangle, square, pentagon, and hexagon.
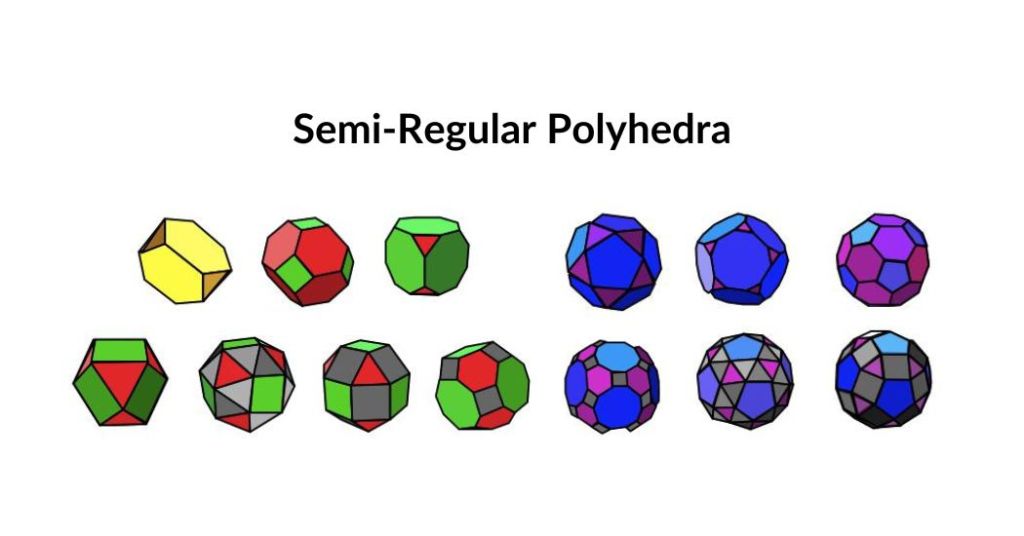
13 Archimedean Solids
There are a total of 13 Archimedean solids, including the truncated tetrahedron, truncated cube, truncated octahedron, truncated dodecahedron, truncated icosahedron, cuboctahedron, rhombicuboctahedron, rhombicosidodecahedron, snub cube, snub dodecahedron, icosidodecahedron, truncated cuboctahedron, and truncated icosidodecahedron.
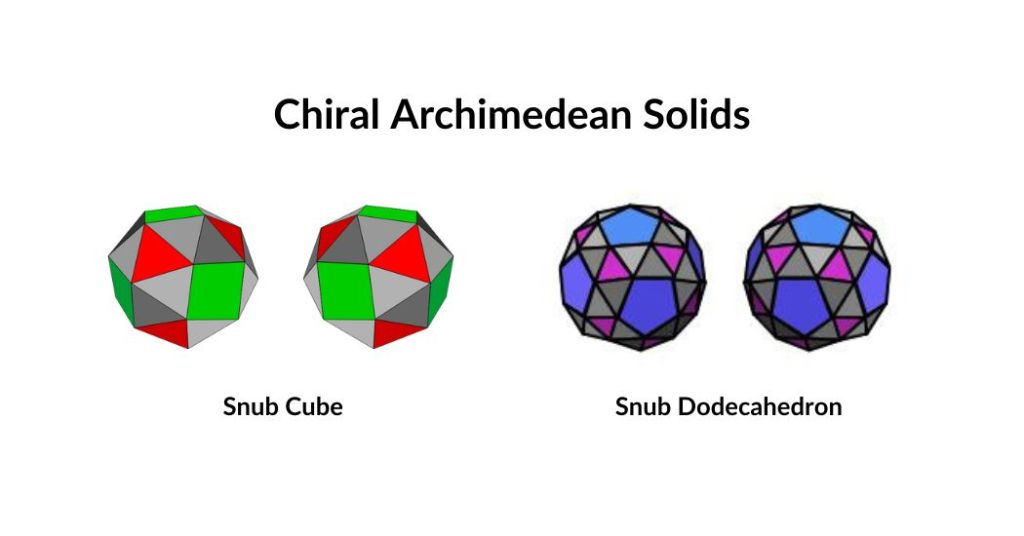
These are two forms, called ‘snubs’, the Snub Cube and Snub Dodecahedron, which are related to one another like a left-hand and a right-hand glove: they are enantiomorphic or call them chiral as in chemistry.
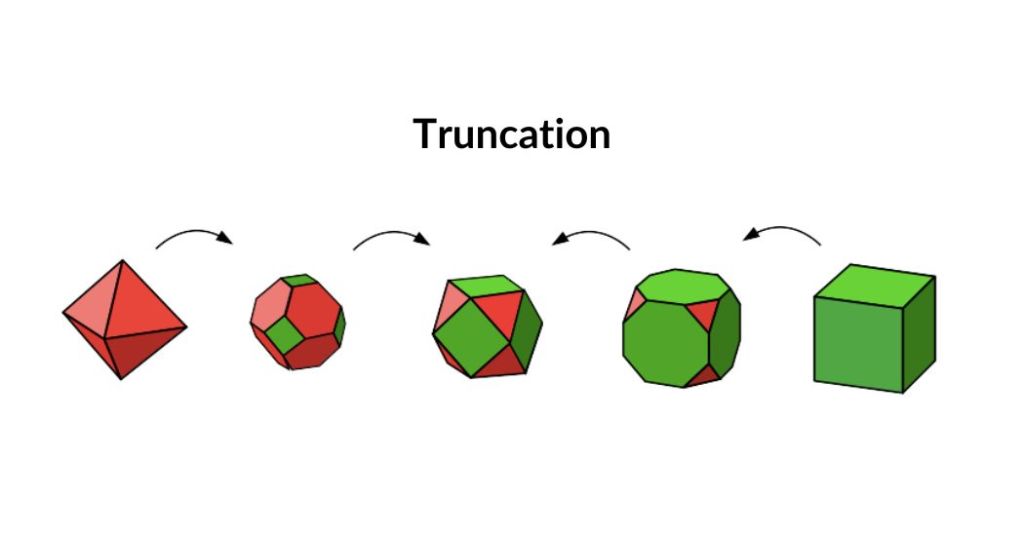
Relationship of Platonic and Archimedean Solids
The Archimedean solids can be derived from the Platonic solids by three geometric process of truncation, explosion, and twisting. Thereby, new faces are created, which modifies the symmetry of the original solid.
The 5 Elements Course
A Journey into 3D
Construct the 5 Platonic Solids in 2D and 3D and discover their novel relationship to the 5 Elements
Carry On Learning
Explore more
geometric principles
This post is part of our Guide to Euclidean Geometry. You can explore more or return to the index page to follow the series in sequential order.
Up Next
The Cuboctahedron
Sacred Geometry is defined as drawing without measurement. It involves the tools of drawing compass…
