Welcome, to this online guide to Euclidean Geometry, produced by In2infinity, and written by Sunil Jenkar. IN the Last Section, we explored the Triangle. In this section, we will explore the nature terminologies associated with squares and rectangles, also known as QUADRILATERALS.
What is a QUADRILATERAL?
A quadrilateral (or quadrangle or quadragon) is a rectilinear figure bound by four straight lines called edges or sides. The word ‘quad’ means four and the word lateral means sides. Quadrilateral also has four angles defined by the points where the edges meet (called vertex).
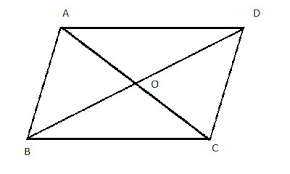
Various Parts of Quadrilateral
Diagonals : It is formed by the segment joined by the opposite vertices.
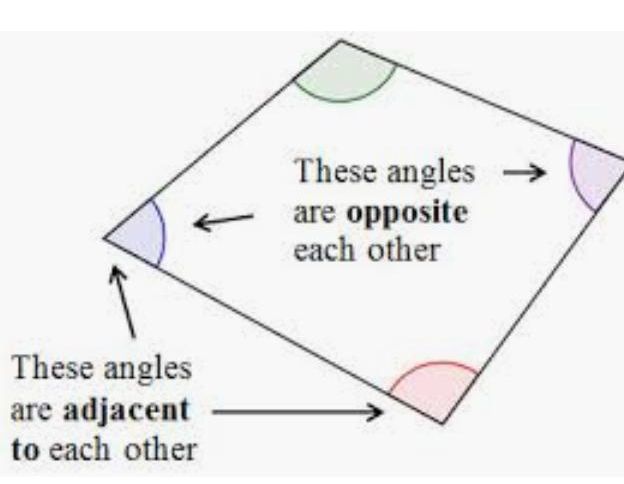
Adjacent angles : Two angles of a quadrilateral are called adjacent angles, if they have a common side as an arm.
Opposite angles : Two angles of a quadrilateral are called opposite angles, which are not adjacent angles.
On the basis of diagonals, there are two types of quadrilaterals.
- Convex quadrilateral: The diagonals intersect in the interior region.
- Concave quadrilateral: One of the diagonal is in the exterior region.
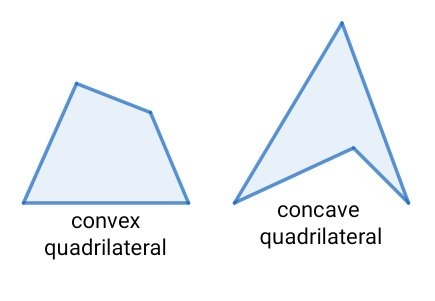
Convex quadrilaterals
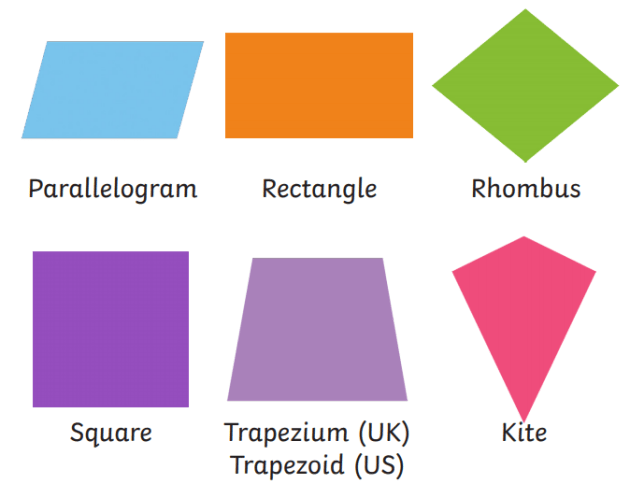
We will only be studying the various types of convex quadrilaterals in the following sections. There are many types of quadrilaterals. They are organized in different classes according to certain characteristics. The most common classes of quadrilaterals are: Parallelogram, Trapezium and Kite (or deltoid).

Parallelogram
A quadrilateral whose opposite sides are pairwise parallel is called a parallelogram. Such a quadrilateral is obtained by intersecting any two parallel lines with two other parallel lines.
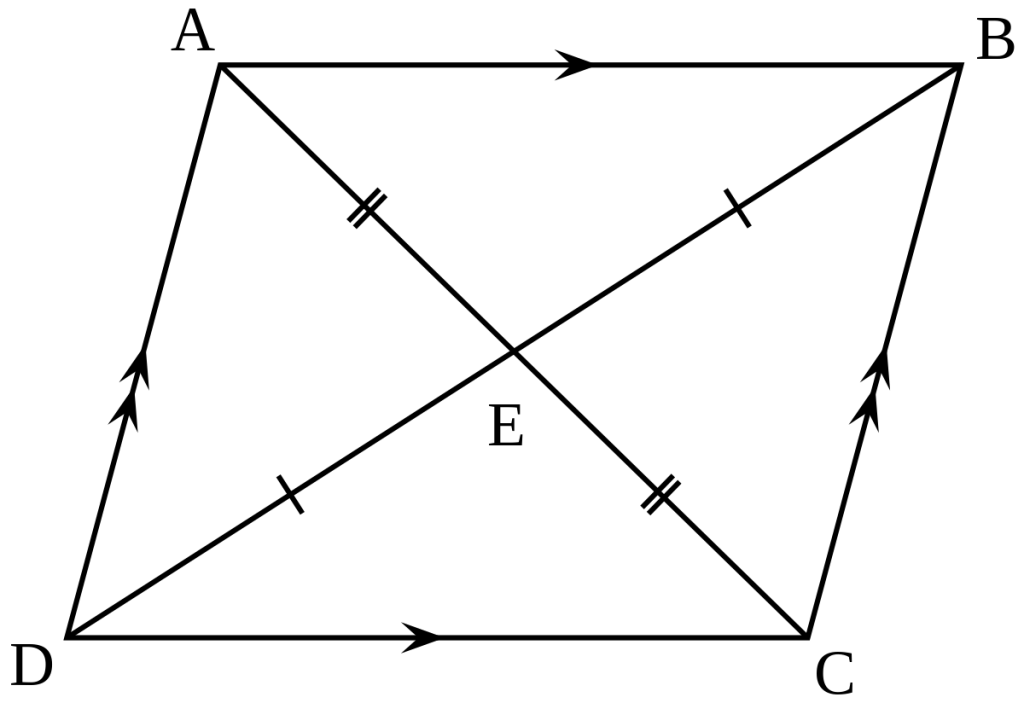
Parallelogram Theorems
1: In any parallelogram, opposite sides are congruent, opposite angles are congruent, and the sum of angles adjacent to one side is two right angles.
Corollary: If one of the angles of a parallelogram is right, then the other three are also right.
2: Conversely, If in a convex quadrilateral, opposite sides are congruent to each other, or two opposite sides are congruent and parallel, then this quadrilateral is a parallelogram.
3: If a quadrilateral is a parallelogram, then its diagonals bisect each other. Vice versa, in a quadrilateral, if the diagonals bisect each other, then this quadrilateral is a parallelogram.
4: Two angles whose sides are parallel each to each are either equal or supplementary.
Corollary: The opposite angles of a parallelogram are equal, and any two consecutive angles are supplementary.
5: The opposite sides of a parallelogram are equal.
6: The diagonals of a parallelogram bisect each other.
7: Two parallelograms are congruent if two sides and the included angle of the one are equal respectively to two sides and the included angle of the other.
Corollary: Two rectangles having equal bases and equal altitudes are congruent.
9: Parallelograms which are on the same base and in the same parallels equal one another.
10: Parallelograms which are on equal bases and in the same parallels equal one another.
11: If a parallelogram has the same base with a triangle and is in the same parallels, then the parallelogram is double the triangle.
Special Parallelogram
Rectangle
When all the angles contained in the parallelogram are right angles it is called a rectangle.
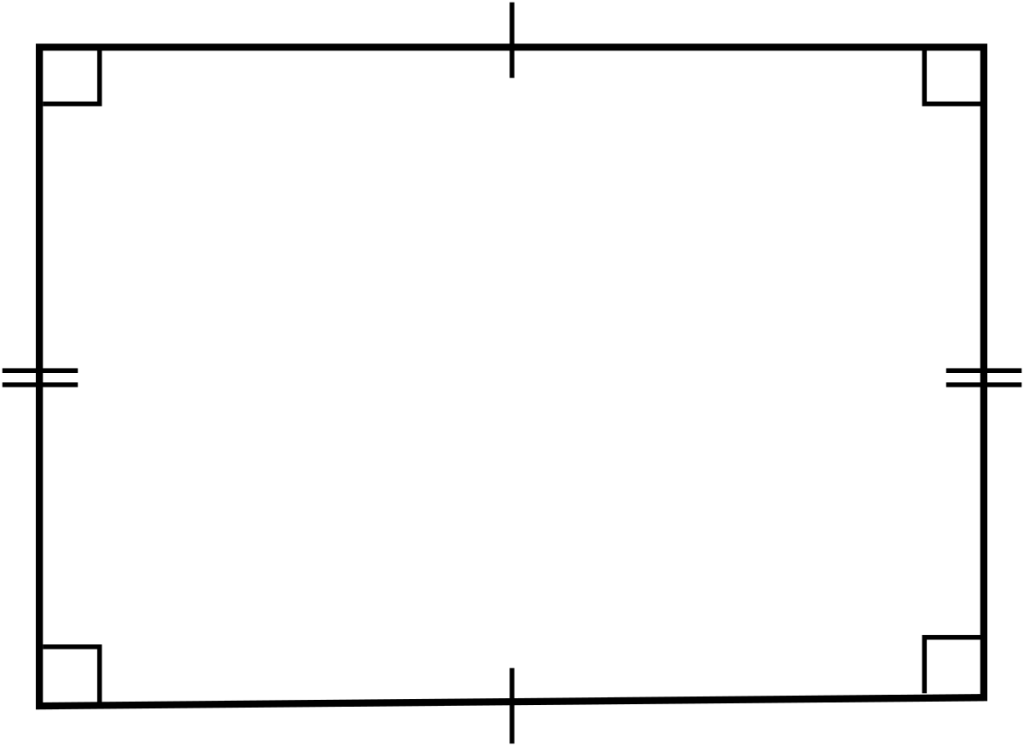
Rectangle Theorems
- Each of the four angles of a rectangle is a right angle.
- The diagonals of a rectangle are of equal length
Rhombus
If all the sides containing the parallelogram are equal to each other, it is called a rhombus.
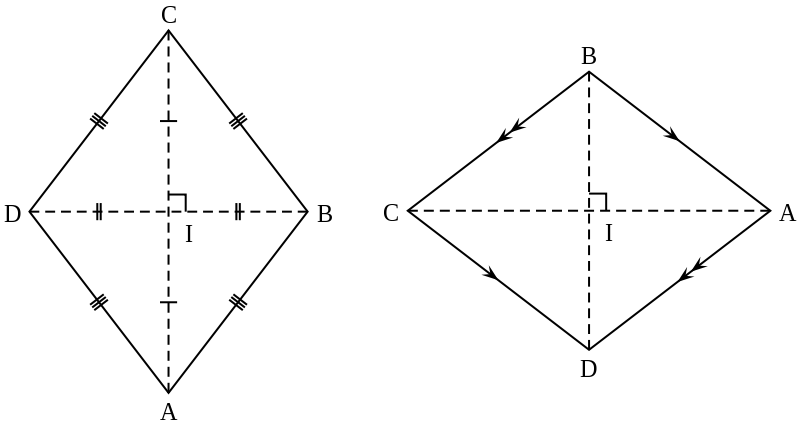
Rhombus Theorem
- The diagonals of a rhombus are perpendicular to each other.
- Conversely, If the diagonals of a parallelogram are perpendicular, then it is a rhombus.
Square
A square is a unique parallelogram which has all sides equal, as well as all angles as right angles. It can be considered a special case of rectangle as well as rhombus.
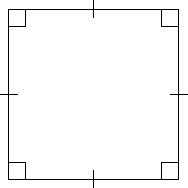
Square Theorems
- The diagonals of a square are equal and perpendicular to each other.
- If the diagonals of a parallelogram are equal and intersect at right angles, then the parallelogram is a square.
Trapezium
When none of the sides containing the quadrilateral are parallel, it is called a trapezium. When two sides of the quadrilateral are mutually parallel, it is called a trapezoid. If the non-parallel sides are equal, in that case the trapezoid is called isosceles. If it is composed of two right angles, then it is referred to as right-angled trapezoid. In modern usage, the term trapezium is often used to imply trapezoid.
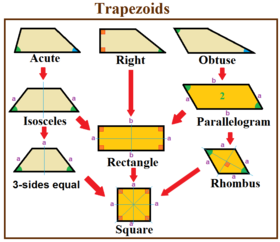
Trapezoid Theorems
- A trapezoid is isosceles if and only if the base angles are congruent.
- A trapezoid is isosceles if and only if the diagonals are congruent.
- If a trapezoid is isosceles, the opposite angles are supplementary.
- The median (or midsegment) of a trapezoid is parallel to each base, and its length is one half the sum of the lengths of the bases.
Kite (Deltoid)
A quadrilateral is a kite,if it has two pairs of equal adjacent sides and unequal opposite sides.
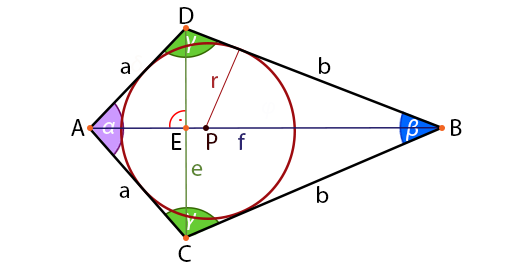
Kite Theorems
- A trapezoid is isosceles if and only if the base angles are congruent.
- A trapezoid is isosceles if and only if the diagonals are congruent.
- If a trapezoid is isosceles, the opposite angles are supplementary.
- The median (or midsegment) of a trapezoid is parallel to each base, and its length is one half the sum of the lengths of the bases.
Polygons in General
A portion of a plane bounded by a broken line is called a polygon. The terms sides, perimeter, angles, vertices, and diagonals are employed in the usual sense in connection with polygons in general.
Polygons classified as to Sides
A polygon is a triangle, if it has three sides; a quadrilateral, if it has four sides; a pentagon, if it has five sides; a hexagon, if it has six sides. These names are sufficient for most cases. The next few names in order are heptagon, octagon, nonagon, decagon, undecagon, dodecagon. A polygon is equilateral, if all of its sides are equal.
Polygons classified as to Angles
A polygon is equiangular, if all of its angles are equal; convex, if each of its angles is less than a straight angle; concave, if it has an angle greater than a straight angle.
Regular Polygon
A polygon that is both equiangular and equilateral is called a regular polygon.
Relation of Two Polygons
Two polygons are mutually equiangular, if the angles of the one are equal to the angles of the other respectively, taken in the same order; mutually equilateral, if the sides of the one are equal to the sides of the other respectively, taken in the same order; congruent, if mutually equiangular and mutually equilateral, since they then can be made to coincide.
Polygon Theorems
- The sum of the interior angles of a polygon is equal to two right angles, taken as many times less two as the figure has sides.
Corollary :
a. The sum of the angles of a quadrilateral equals four right angles; and if the angles are all equal, each is a right angle.
b. Each angle of a regular polygon of n sides is equal to (n – 2)/n right angles.
2 The sum of the exterior angles of a polygon, made by producing each of its sides in succession, is equal to four right angles.
Generalized Mid-Point/Intercept Theorem
If three or more parallels intercept equal segments on one transversal, they intercept equal segments on every transversal.
Corollary
- If a line is parallel to one side of a triangle and bisects another side, it bisects the third side also.
- The line which joins the mid-points of two sides of a triangle is parallel to the third side, and is equal to half the third side.
- The line joining the mid-points of the non-parallel sides of a trapezoid is parallel to the bases and is equal to half the sum of the bases.
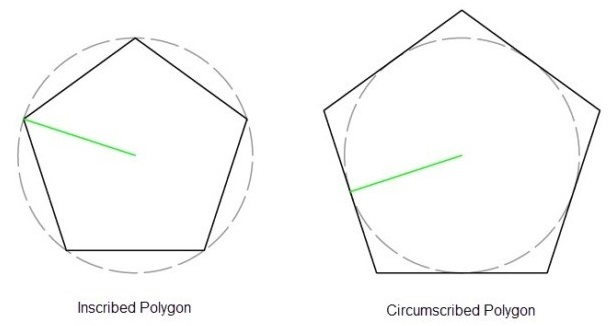
Inscribed Polygons
An inscribed polygon is a polygon in which all vertices lie on a circle. The polygon is inscribed in the circle, and the circle is circumscribed about the polygon. It is a polygon in a circle.
A circumscribed polygon is a polygon in which each side is a tangent to a circle. The circle is inscribed in the polygon, and the polygon is circumscribed about the circle. It is a polygon outside the circle, or in other words, the circle is inside a polygon.
Mensuration is the part of geometry that is concerned with ascertaining lengths, areas, and volumes. Mensuration concerns with the measurement of the geometric figures and their parameters like length, volume, shape, surface area, lateral surface area, etc.
Perimeter of polygons
Perimeter can be defined as the total length of the boundary of a geometrical figure. Area is the measure of the surface contained inside a geometrical figure. It is generally measured against the unit square, or say, how much surface in comparison with a square of unit side length.
Glossary of Definitions
Quadrilaterals
A quadrilateral is a rectilinear figure bound by four straight lines called edges or sides. Quadrilateral also has four angles defined by the points where the edges meet (called vertex).
Kinds of quadrilaterals:
Trapezium: When none of the sides containing the quadrilateral are parallel.
Trapezoid: When two sides of the quadrilateral are mutually parallel, it is called a trapezoid. If the non parallel sides are equal in that case the trapezoid is called isosceles.
Parallelogram: If the pair of opposite sides are parallel, such quadrilateral is called a parallelogram. Kinds of parallelogram:
Rectangle: When all the angles contained in the parallelogram are right angles it is called a rectangle.
Rhombus: If all the sides containing the parallelogram are equal to each other, it is called a rhombus.
Square: A square is a unique parallelogram which has all sides equal, as well as all angles as right angles. It can be considered a special case of rectangle as well as rhombus.
Higher-Polygons
A circle is a closed curve lying in a plane such that all of its points are at equal distance from a fixed point in the plane (called the centre of the circle).
Radius: A straight line from the centre of the circle.
Diameter: A straight line through the centre, terminating at each end of the circle.
Arc: A portion of the circle is called an arc. An arc equal to half of the circle is called a semicircle. An arc less than the semicircle is called a minor arc, while an arc greater than the semicircle is called a major arc.
Chords, Secants and Tangents
Secant: A line intersecting a circle in two places is referred to as a secant.
Chord: The portion of secant that is contained within the circle is called a chord.
Tangent: If a line intersects (touches) a circle at only one single point, it is called a tangent.
Explore more
geometric principles
This post is part of our Guide to Euclidean Geometry. You can explore more or return to the index page to follow the series in sequential order.
Up Next

Fundamentals
PrevPreviousThe Ultimate Guide to Geometry NextRudimentsNext Introduction Geometry can be defined as a quantitative and…





