Welcome, to this online guide to Euclidean Geometry, produced by In2infinity, and written by Sunil Jankar. This topic is covered in three different sections. First section covers general properties of regular polygons, the second section covers some classic Euclidean constructions of inscribed regular polygons and finally we will cover the areas of polygons.
General Properties of Regular Polygons
Definitions
Regular Polygon
A polygon that is both equiangular and equilateral is called a regular polygon. Familiar examples of regular polygons are the equilateral triangle and the square.

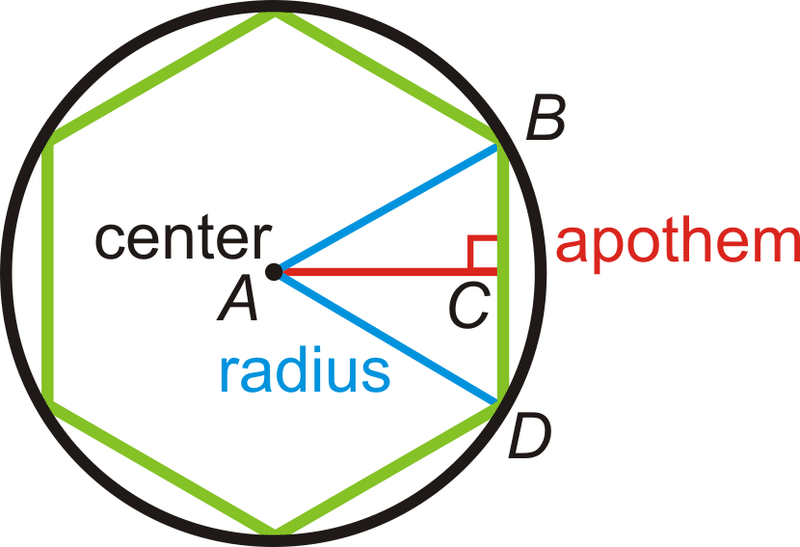
Inscribed Polygon
A rectilinear figure is said to be inscribed in a circle when each angle of the inscribed figure lies on the circumference of the circle.

Circumscribed Polygon
A rectilinear figure is said to be circumscribed about a circle when each side of the circumscribed figure touches the circumference of the circle.
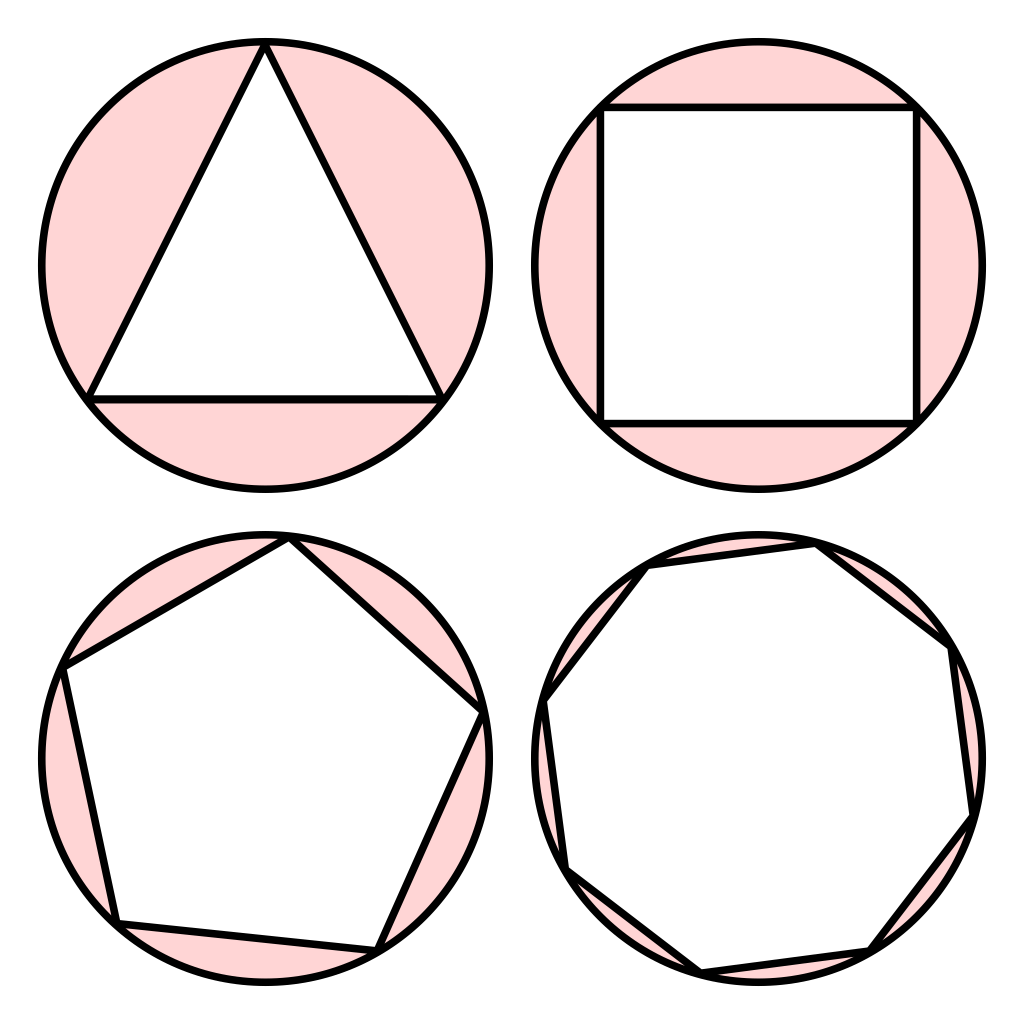
Radius
The radius of the circle circumscribed about a regular polygon is called the radius of the polygon.
Apothem
The radius of the circle inscribed in a regular polygon is called the apothem of the polygon. The apothem is evidently perpendicular to the side of the regular polygon.
Center
The common centre of the circles circumscribed about and inscribed in a regular polygon is called the centre of the polygon.
Angle at the Center
The angle between the radii drawn to the extremities of any side of a regular polygon is called the angle at the centre of the polygon.
Polygon Theorems
Theorem 1
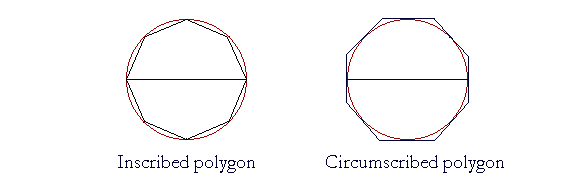
A circle may be circumscribed about, and a circle may be inscribed in any regular polygon.
Corollary
- The radius drawn to any vertex of a regular polygon bisects the angle at the vertex.
- The angles at the center of any regular polygon are equal, and each is supplementary to an interior angle of the polygon.
- An equilateral polygon inscribed in a circle is a regular polygon.
- An equiangular polygon circumscribed about a circle is a regular polygon.
Theorem 2
If a circle is divided into any number of equal arcs, the chords joining the successive points of division form a regular inscribed polygon; and the tangents drawn at the points of division form a regular circumscribed polygon.

Corollary
- Tangents to a circle at the vertices of a regular inscribed polygon, form a regular circumscribed polygon of the same number of sides.
- Tangents to a circle at the mid-points of the arcs subtended by the sides of a regular inscribed polygon form a regular circumscribed polygon, whose sides are parallel to the sides of the inscribed polygon and whose vertices lie on the radii (produced) of the inscribed polygon.
- Lines drawn from each vertex of a regular polygon to the mid-points of the adjacent arcs subtended by the sides of the polygon, form a regular inscribed polygon of double the number of sides.
- Tangents at the mid-points of the arcs between adjacent points of contact of the sides of a regular circumscribed polygon, form a regular circumscribed polygon of double the number of sides.
- The perimeter of a regular inscribed polygon is less than that of a regular inscribed polygon of double the number of sides; and the perimeter of a regular circumscribed polygon is greater than that of a regular circumscribed polygon of double the number of sides.
Theorem 3
Two regular polygons of the same number of sides are similar.
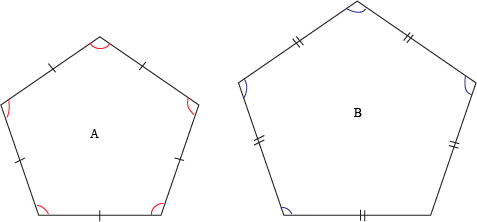
Corollary
The areas of two regular polygons of the same number of sides are to each other as the squares on any two corresponding sides.
Theorem 4
The perimeters of two regular polygons of the same number of sides are to each other as their radii, and also as their apothems.
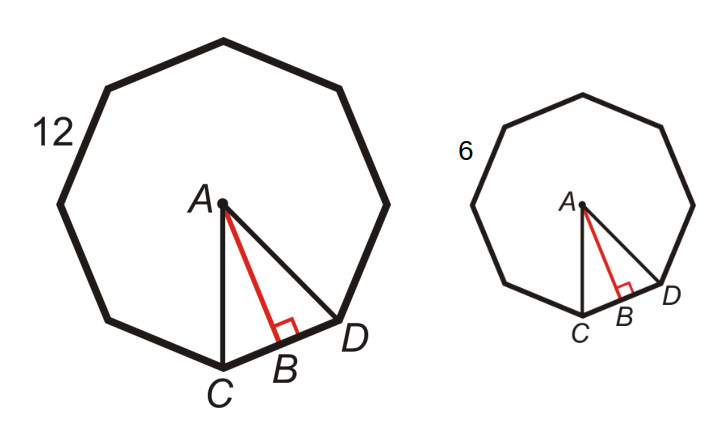
Corollary
The areas of two regular polygons of the same number of sides are to each other as the squares on the radii of the circumscribed circles, and also as the squares on the radii of the inscribed circles.
Theorem 5
If the number of sides of a regular inscribed polygon is indefinitely increased, the apothem of the polygon approaches the radius of the circle as its limit.
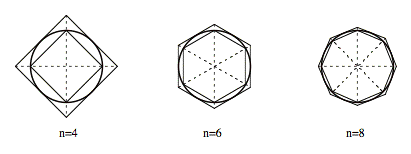
Corollary
If the number of sides of a regular inscribed polygon is indefinitely increased, the square on the apothem approaches the square on the radius of the circle as its limit.
Theorem 6
An arc of a circle is less than a line of any kind that envelops it on the convex side and has the same extremities.
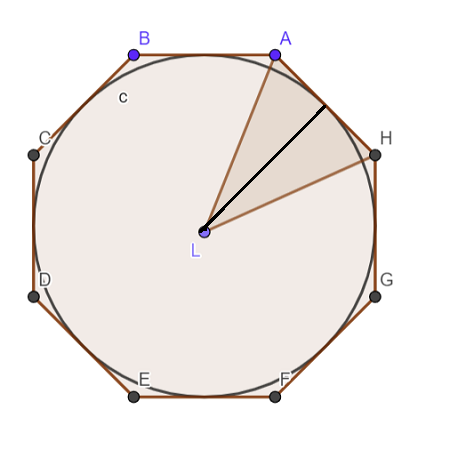
Corollary
A circle is less than the perimeter of any polygon circumscribed about it.
Theorem 7
Two circumferences have the same ratio as their Radii.

Corollary
- The ratio of any circle to its diameter is constant. The constant ratio of a circle to its diameter is represented by the Greek letter π (pi).
- In any circle, the circumference = 2πr.
Classic Euclidean Constructions
Problem 1
To inscribe a triangle equiangular with a given triangle in a given circle.
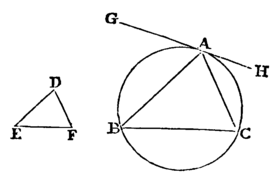
Let ABC be the given circle, and DEF the given triangle.
It is required to inscribe a triangle equiangular with the triangle DEF in the circle ABC.
Draw tangent line GH touching the circle ABC at A.
Construct the angle HAC equal to the angle DEF on the straight line AH and at the point A on it, and construct the angle GAB equal to the angle DFE on the straight line AG and at the point A on it. Join BC.
Then, since a straight line AH touches the circle ABC, and from the point of contact at A, the straight line AC is drawn across in the circle, therefore the angle HAC equals the angle ABC in the alternate segment of the circle.
But the angle HAC equals the angle DEF, therefore the angle ABC also equals the angle DEF.
For the same reason the angle ACB also equals the angle DFE, therefore the remaining angle BAC also equals the remaining angle EDF.
Therefore, a triangle equiangular with the given triangle has been inscribed in the given circle.
It is worth mentioning that the above generalized construction can be used to inscribe an equilateral triangle in a circle.
Problem 2
To inscribe a square in a given circle.
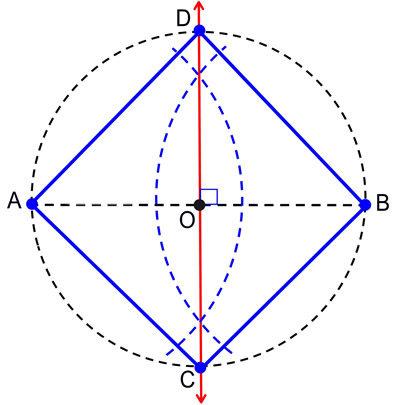
Let ABCD be the given circle.
It is required to inscribe a square in the circle ABCD.
Draw two diameters AC and BD of the circle ABCD at right angles to one another, and join AB, BC, CD, and DA.
Then, since BE equals ED, for E is the centre, and EA is common and at right angles, therefore the base AB equals the base AD.
For the same reason, each of the straight lines BC and CD also equals each of the straight lines AB and AD. Therefore, the quadrilateral ABCD is equilateral.
It is also right-angled. For, since the straight line BD is a diameter of the circle ABCD, therefore BAD is a semicircle, therefore the angle BAD is right.
For the same reason, each of the angles ABC, BCD, and CDA is also right. Therefore, the quadrilateral ABCD is right-angled.
But it was also proved equilateral, therefore it is a square, and it has been inscribed in the circle ABCD.
Therefore, the square ABCD has been inscribed in the given circle.
Problem 3
To inscribe an equilateral and equiangular pentagon in a given circle.
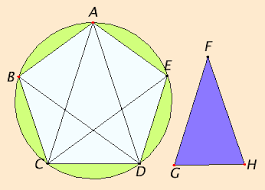
Let ABCDE be the given circle.
It is required to inscribe an equilateral and equiangular pentagon in the circle ABCDE.
Set out the isosceles triangle FGH having each of the angles at G and H double the angle at F.
Inscribe in the circle ABCDE the triangle ACD equiangular with the triangle FGH, so that the angles CAD, ACD, and CDA equal the angles at F, G, and H respectively. Therefore, each of the angles ACD and CDA is also double the angle CAD.
Now bisect the angles ACD and CDA respectively by the straight lines CE and DB, and join AB, BC, DE, and EA.
Then, since each of the angles ACD and CDA is double the angle CAD, and they are bisected by the straight lines CE and DB, therefore the five angles DAC, ACE, ECD, CDB, and BDA equal one another.
But equal angles stand on equal circumferences, therefore the five circumferences AB, BC, CD, DE, and EA equal one another.
But straight lines that cut off equal circumferences are equal, therefore the five straight lines AB, BC, CD, DE, and EA equal one another. Therefore, the pentagon ABCDE is equilateral.
It is also equiangular. For, since the circumference AB equals the circumference DE, add BCD to each, therefore the whole circumference ABCD equals the whole circumference EDCB.
And the angle AED stands on the circumference ABCD, and the angle BAE on the circumference EDCB, therefore the angle BAE also equals the angle AED.
For the same reason each of the angles ABC, BCD, and CDE also equals each of the angles BAE and AED, therefore the pentagon ABCDE is equiangular.
But it was also proved equilateral, therefore an equilateral and equiangular pentagon has been inscribed in the given circle.
Problem 4
To inscribe a regular hexagon in a given circle.
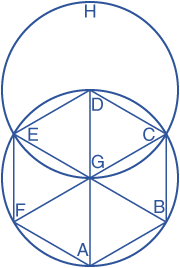
Let ABCDEF be the given circle. It is required to inscribe an equilateral and equiangular hexagon in the circle ABCDEF.
Draw the diameter AD of the circle ABCDEF. Take the centre G of the circle. Describe the circle EGCH with center D and radius DG. Join EG and CG and carry them through to the points B and F. Join AB, BC, CD, DE, EF, and FA.
The hexagon ABCDEF is equilateral and equiangular. For, since the point G is the centre of the circle ABCDEF, GE equals GD.
Again, since the point D is the center of the circle GCH, DE equals DG.
But GE was proved equal to GD, therefore GE also equals ED. Therefore, the triangle EGD is equilateral, and therefore its three angles EGD, GDE, and DEG equal one another, inasmuch as, in isosceles triangles, the angles at the base equal one another.
And the sum of the three angles of the triangle equals two right angles, therefore the angle EGD is one-third of two right angles.
Similarly, the angle DGC can also be proved to be one third of two right angles.
And, since the straight line CG standing on EB makes the sum of the adjacent angles EGC and CGB equal to two right angles, therefore the remaining angle CGB is also one-third of two right angles.
Therefore, the angles EGD, DGC, and CGB equal one another, so that the angles vertical to them, the angles BGA, AGF, and FGE, are equal.
Therefore, the six angles EGD, DGC, CGB, BGA, AGF, and FGE equal one another.
But equal angles stand on equal circumferences, therefore the six circumferences AB, BC, CD, DE, EF, and FA equal one another
And straight lines that cut off equal circumferences are equal, therefore the six straight lines equal one another. Therefore, the hexagon ABCDEF is equilateral.
It is also equiangular. For, since the circumference FA equals the circumference ED, add the circumference ABCD to each, therefore the whole FABCD equals the whole EDCBA. And the angle FED stands on the circumference FABCD, and the angle AFE on the circumference EDCBA, therefore the angle AFE equals the angle DEF.
Similarly, it can be proved that the remaining angles of the hexagon ABCDEF are also severally equal to each of the angles AFE and FED, therefore the hexagon ABCDEF is equiangular.
But it was also proved equilateral, and it has been inscribed in the circle ABCDEF.
Therefore, an equilateral and equiangular hexagon has been inscribed in the given circle.
Areas of Polygons
DEFINITIONS
Unit of Surface
A square the side of which is a unit of length is called a unit of surface.
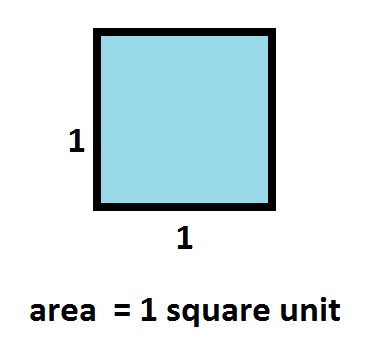
Area of a Surface
The measure of a surface, expressed in units of surface, is called its area.
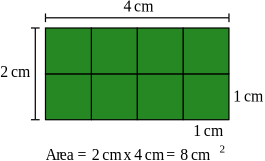
Theorems - Suface area
Trinagle
Theorem 1
The area of a triangle is equal to half the product of its base by its altitude.
Corollary
- Triangles having equal bases and equal altitudes are equivalent.
- Triangles having equal bases are to each other as their altitudes; triangles having equal altitudes are to each other as their bases; any two triangles are to each other as the products of their bases by their altitudes.
- The product of the sides of a right triangle is equal to the product of the hypotenuse by the altitude from the vertex of the right angle.
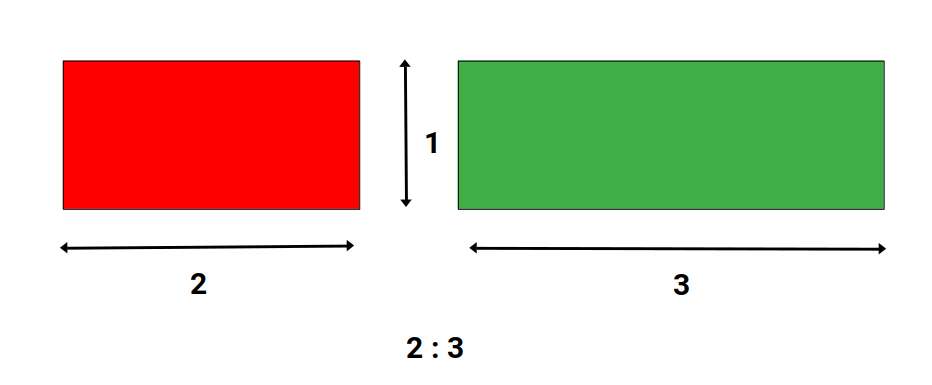
Rectangles
Theorem 2
Two rectangles having equal altitudes are to each other as their bases.
Corollary
Two rectangles having equal bases are to each other as their altitudes.
Theorem 3
Two rectangles are to each other as the products of their bases by their altitudes.
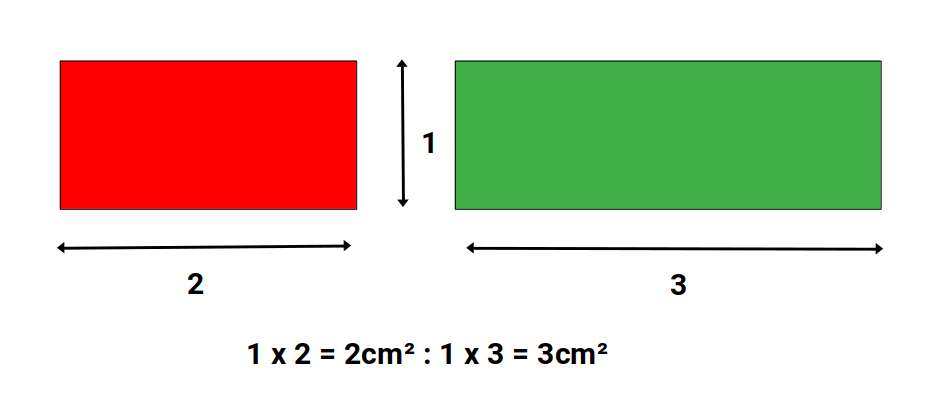
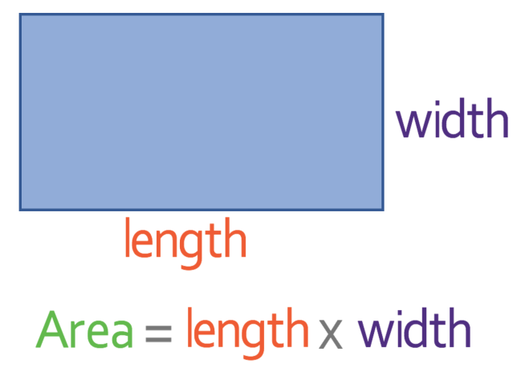
Theorem 4
The area of a rectangle is equal to the product of its base by its altitude.
Parallelogram
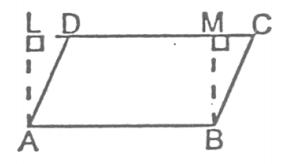
Theorem 5
The area of a parallelogram is equal to the product of its base by its altitude.
Corollary
- Parallelograms having equal bases and equal altitudes are equivalent.
- Parallelograms having equal bases are to each other as their altitudes; parallelograms having equal altitudes are to each other as their bases; any two parallelograms are to each other as the products of their bases by their altitudes.
Rhombus
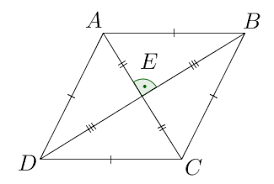
Theorem 6
The area of a rhombus is equal to half the product of its diagonals.
Trapezoid
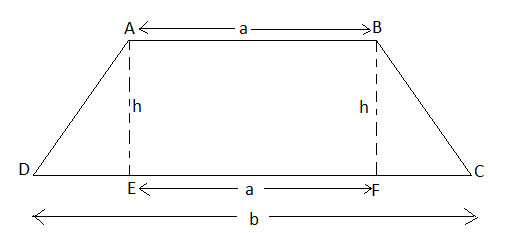
Theorem 7
The area of a trapezoid is equal to half the product of the sum of its bases by its altitude.
Corollary
The area of a trapezoid is equal to the product of the line joining the mid-points of its non-parallel sides by its altitude.
Irregular Polygons
Theorem 8
The area of an irregular polygon may be found by dividing the polygon into triangles, and then finding the area of each of these triangles separately.

Circle
Theorem 9
The area of a circle is equal to half the product of its radius by its circumference.
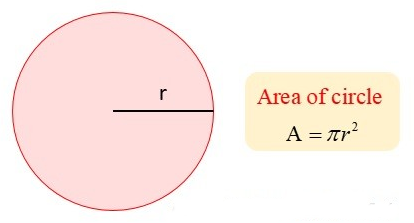
Corollary
- The area of a circle is equal to π times the square on its radius.
- The areas of two circles are to each other as the squares on their radii.
- The area of a sector is equal to half the product of its radius by its arc.
Miscellaneous Theorems
Theorem 10
The areas of two similar triangles are to each other as the squares on any two corresponding sides.
Theorem 11
The areas of two similar polygons are to each other as the squares on any two corresponding sides.
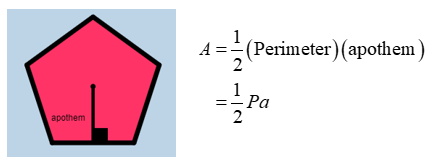
Theorem 12
The area of a regular polygon is equal to half the product of its apothem by its perimeter.
Theorem 13
The area of a circumscribed polygon is equal to half the product of its perimeter by the radius of the inscribed circle.
Explore more
geometric principles
This post is part of our Guide to Euclidean Geometry. You can explore more or return to the index page to follow the series in sequential order.
Up Next

Rudiments
Welcome, to this online guide to Euclidean Geometry, produced by In2infinity, and written by Sunil…






