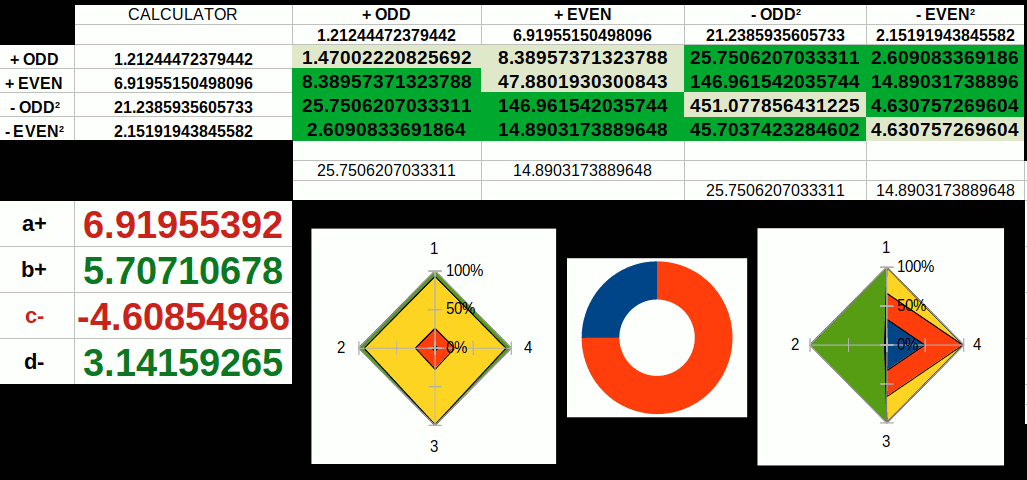
4D Maths is a fundamental step into a new dimension of mathematics. Founded upon the idea of space, time and dimension, and the infinity equation, 0 ±1= ±∞, the 4D calculator generates new insight into the infinite nature of numbers, and introduces the ‘Theory of Effort’.
Overview
How numbers are created
4D Maths suggest a new type of categorisation of number at the axiomatic level. Based on the notion that infinity is created from zero to which one is added or subtracted, and the result reiterated on into infinity. This creates a loop that leads to infinity, in either the negative or positive direction. The loop breaks when the opposite action, either addition or subtraction, reverses one step on the number line, creating a manifest value. All whole numbers are derived in this way, as numerical values only make sense when the preceding units are present.
Effort Values
The number of times a calculation is reiterated determines its effort value. The Theory of Effort examines how many times something needs to occur, such as an iteration of a calculation, in order to determine a specific value.
Space numbers
Numbers termed ‘Space’ are considered to initiate from ZERO. The positive and negative values are a movement, in terms of numerical distance. This is a new categorisation of number that might be confused with the existing idea of cardinal ‘counting’ numbers. Spacial numbers include zero in the set, and measure relative distance from a central point, rather than counting objects in space.
Time numbers
In Geometric Maths, the origins of mathematical beginnings is ascribed to the division of zero. This mathematical operation creates a pair of infinite positive and negative infinities.
The next number type is based on time, where a number is operated upon to generate an outcome. As division is the first mathematical operator to effect space, we can perceive them as a function of time, that changes the result (state) of the space number.
Space changes over time, and so time numbers are always seen to divide space, whether plus or minus.
Dimension Numbers
The final number set is based on the notion of dimension. By this, we mean the distance scale. For example, dimension +1 will increase a step by 1, creating a uniform scale, such as is found in the sequence of whole numbers. Whereas, dimension +2 will create a scale at half the density, such as in the 2× multiplication table. This we call this the ‘infinite density function‘, which is the notion of a line that contains an infinite set express at a specific scale.

This completes the 4D equation that is the basis of the 4D calculator, used to explore this fascinating mathematical landscape.
Download our 4D Calculator
Linux, MAC, WINDOWS
Learn more about Our Theory of Geometric Maths
The axiomatic concepts of 4D Maths are derived from our Geometric Maths. You can learn more about this background by reading more articles on this site.
The Zero Boundary
The Zero Boundary divides the infinite sets of positive and negative numbers, and is defined…
Reciprocal number space
All numbers beyond ONE have a reciprocal representation between the numbers ZERO and ONE. It…
What is the continuum hypothesis?
The Continuum Hypothesis was the #1 mathematical challenge set by Hilbert at the start of…
THE
Concept
dissolving Numbers
4D Maths employs the equation:
(±S / ±T) ± D = n
This calculation is reiterated to create a numerical series that either explodes into infinity (gets infinitely bigger) or diminishes towards a specific value. With each iteration, the number becomes defined to a greater degree. We count the number of iterations, termed the effort value, which denotes a particular value that is completely dependent on its initial starting point (the space number).
We can graph the number as it diminishes toward a specific value, this we call a dissolution wave.
Every single number produces a unique infinity signature as it dissolves or explodes into infinity. This is determined by the configuration of the calculator that is counted to a specific effort value. More advanced 4D calculators can ‘modulate’, through a specific set of effort values at a specified time rate, thereby animating the characteristics of the dissolution wave.
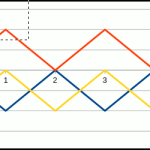
4 types of dissolution wave
Number Lines
By dissolving a number towards infinity using the 4D Maths equation, we can set up the calculator to operate in a certain way. In its most simple configuration, we can choose whether the dimensional number in the calculator is added or subtracted from the total.
Number Lines
As 4D maths uses effort values to track the number of iterations, we do not consider numbers as a single unit, rather a collection of infinite decimal fraction, that each relate to the origin. For this reason we call each calculator setting a line, that is an infinite set of numbers, each of which is unique to the space, time, and dimension, numbers defined at the origin.
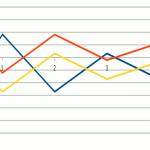
Additive Lines
If the dimensional value of the 4D Maths equation is set only to + then we call it an ‘additive line’.
Subtractive Lines
If the dimensional value is set only to – then we call it a ‘subtractive line’.
Mixed Lines
In more advanced calculators number lines can be composed of both positive and negative dimensional numbers, These can alternate, or be formed of short repeating patterns. There are an infinite number of the ‘mixed line’ possibilities, each of which will produce a unique infinity signature output for any real number.
4D Calculations
Number lines can be combined to form calculations such as multiplication. In this way, we are able to combine the results of two or more dissolution waves, forming a completely new wave. There are numerous ways to combine the infinity signature of any amount of number lines, just like any standard algebraic equation.
However, in 4D maths we can change the setting on the number line and even modulate it through a set of effort values at a certain rate, to form interference and coherence in the dissolution wave.
What no Algebra?
It is an interesting fact that standard algebraic equations readily fail once the time and dimension numbers are changed.
Binary Code
When the times and dimension functions are set to -1, a number line will produce an alternating wave pattern. This is translated into binary code when the space number is set to zero.
Standard Maths
When a subtractive line has its time and dimension values set to -1, its space value will act exactly like a standard number. In this condition, algebra works coherently.
Non-Algebraic equations
An additive line with the same time and dimension settings will create a result that is in the negative of the space input. If we change either the time or dimension values, then the number dissolves, radically changing the result of even the simplest equation.
This table shows the results of the first 10 whole number waves, that dissolve to a new number based on changing the time number on the 4D calculator
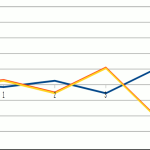
Number Bounce points
When two number lines are compared, often we find an intersection point between them. This can even occur between a particular iteration (effort steps). In some cases the intersection points do not cross each other, instead, they change direction and ‘bounce‘ off each other.
All numbers have a bounce point
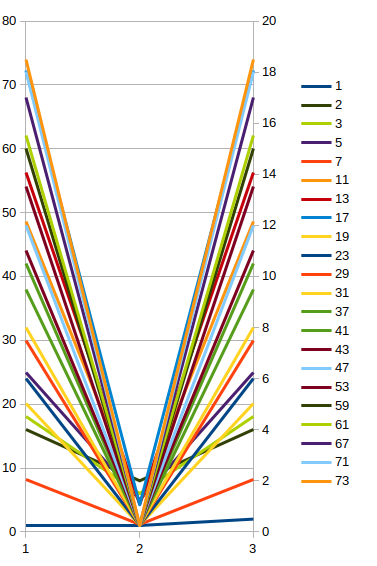

Prime number bounce points data set
The above images show the bounce points of the first 21 primes
Within the infinite set of real numbers, certain values have a particular relationship to their reciprocal number, such as golden and silver numbers. The number π and e also produce interesting results.
Advanced Geometric Mapping.
Advance uses of the 4D calculator scale the wave output onto the hexagonal or square number plain. This allows us to create an analysis of interesting mathematical numbers. By mapping the intersection of number lines as they dissolve towards a point of infinity, we can create geometric 2D forms that can be arranged into a mandala that expresses the nature of their relationship.
Primes and cross calculation
As 4D maths employs the concept of effort values, it exposes a new kind of mathematical space unlike anything conventional mathematics has experienced. As numbers dissolve at different rates, each effort value will produce a slightly different result. We can cross calculate the results and extract a new set of results. These calculations often have extremely unexpected results. Number such as primes are distributed throughout the mathematical space in an apparently arbitrary manner. This leads us to question some of the most fundamental axioms of traditional mathematics.
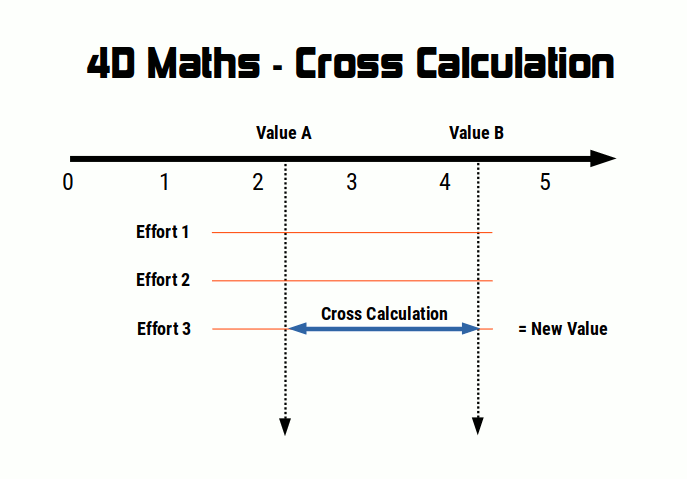
A numerical space within infinity
4D Maths explores the nature of infinity by creating dissolution number waves that devolve to a specific value. We can re-enter these ‘end points’ and use them as the value for another number line.
Each number line devolves toward two values. The first is taken from the result after the space number is divided by time, and the second from after the dimension number is added or subtracted to the value.
Using these pairs of endpoints, it is also possible to ‘evolve’ a number back to its original state.
In this way we can traverse a new kind of number line depending on whether we evolve, or devolve the number by choosing one or other of the two endpoints.
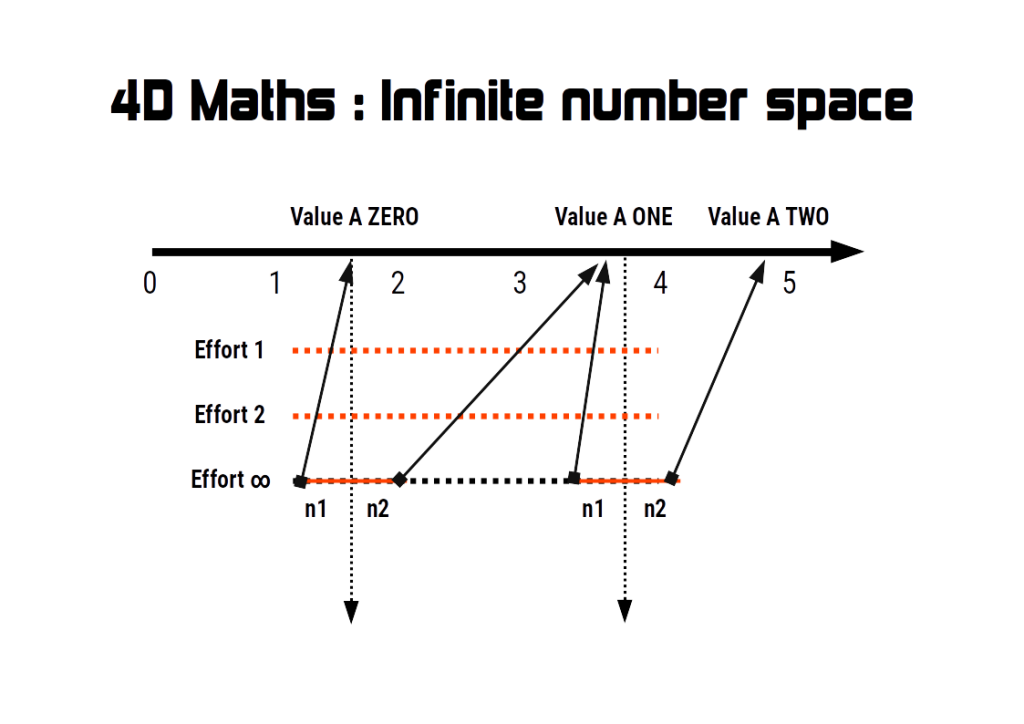
New new mathematical horision
4D Maths is a relatively new discovery, developed by Colin Power and in2infinity. It has its axiomatic foundations in the concept of Geometric Maths, which examines the deeper characteristics of number through a multidimensional perspective.
This extends the notion of a number line into higher dimensional spaces. The expression of infinite signatures can also be complied into higher dimensional forms. These forms can be animated by modulating effort values, which in turn can dynamically model numerical space in orders of 4th dimension and higher.
THE
Conclusion
4D Maths offers a new approach to number that explores its infinite nature.
The 4D Calculator can produce wave like behaviours and model high dimensional geometric number spaces.
Carry on Learning
This post form part of our new theory of 4D Maths by browsing the post below.


Mathematics without algebra
Central to mathematics and science is algebra. Yet 4D Maths suggests that x + y = z might not be such an immutable principle as we first thought.

The Theory of Effort
The Theory of Effort forms part of our new concept of 4D maths. Using this powerful technology, we are able to track numbers as they evolve through recursive calculation.
'SOLVING THE INFINITE'
In2infinity's new solution
to the Continuum Hypothesis.
Listed as the most important mathematical challenge of the 1900s, In2infinity sheds new light on the answer, disproving the present solution, and opening the doors for a whole new math of infinity.