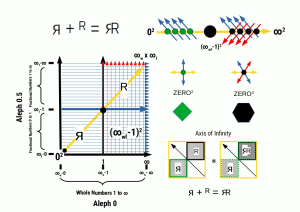
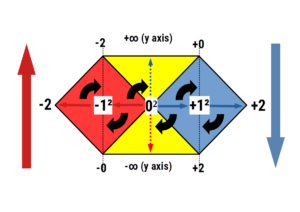
Geometric Maths – Axioms and Definitions
Explore the foundational principles of geometric mathematics with a focus on axioms and definitions. Understand the core concepts that form the basis of geometric theory, including the nature of points, lines, planes, and shapes. Delve into the structured world of geometry where precise definitions and logical axioms guide mathematical reasoning and proofs. Perfect for students, educators, and enthusiasts looking to deepen their understanding of geometric principles.