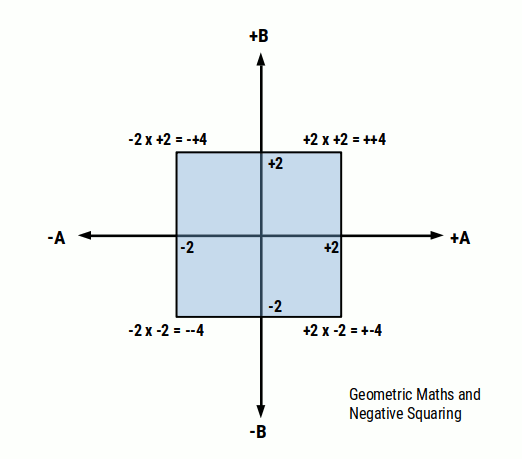
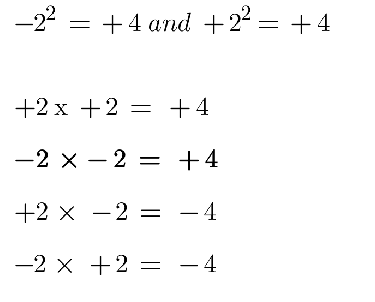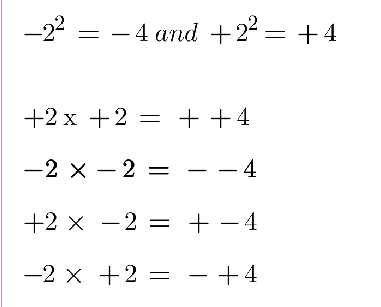In traditional mathematics, the nature of square numbers can only produce a positive result. However, in Geometric Maths, we allow for negative squaring due to the construct of the rotation of the number line.
Overview
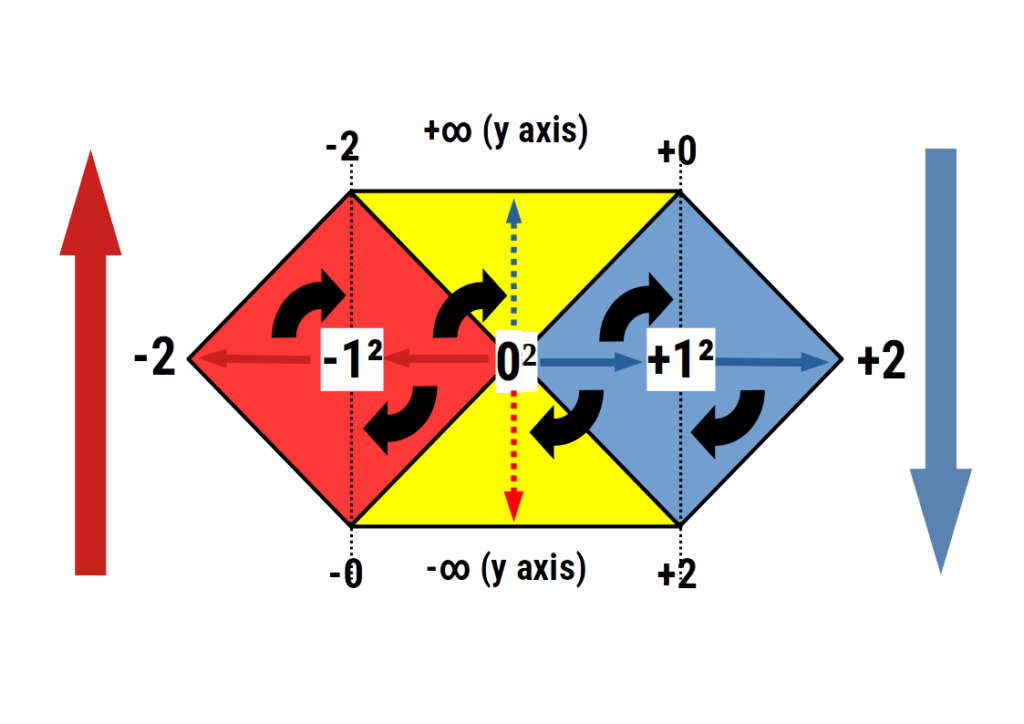
In geometric maths, we explore the concept of Zero² and rotational squaring. This produces the construct of a number cross, which divided a number plane into 4 distinct parts.
In order to qualify each of these number spaces, we use the notation of, ++, – -, + -, and – + for each quadrant. This allows for the number in each space to be multiplied by each other so that negative and positive values results are positioned within a particular quadrant on the 2D plane. This allows for negative square numbers to be calculated.
KEy Points
-
When we employ a 2D number space we can accommodate for both positive and negative square numbers.
-
This allows us to perform simultaneous calculations in 4 distinct number spaces
-
As traditional mathematics does not account for negative squaring, fractal object such as the mandelbrot set appear lopsided.
Review these concepts
If you are not familiar with the concept of Zero² and our other mathematical concepts you can review them before reading on.
4D Squaring
4D squaring demonstrates how dimensionality can be increased through powers, and offers a solution to…
Zero²
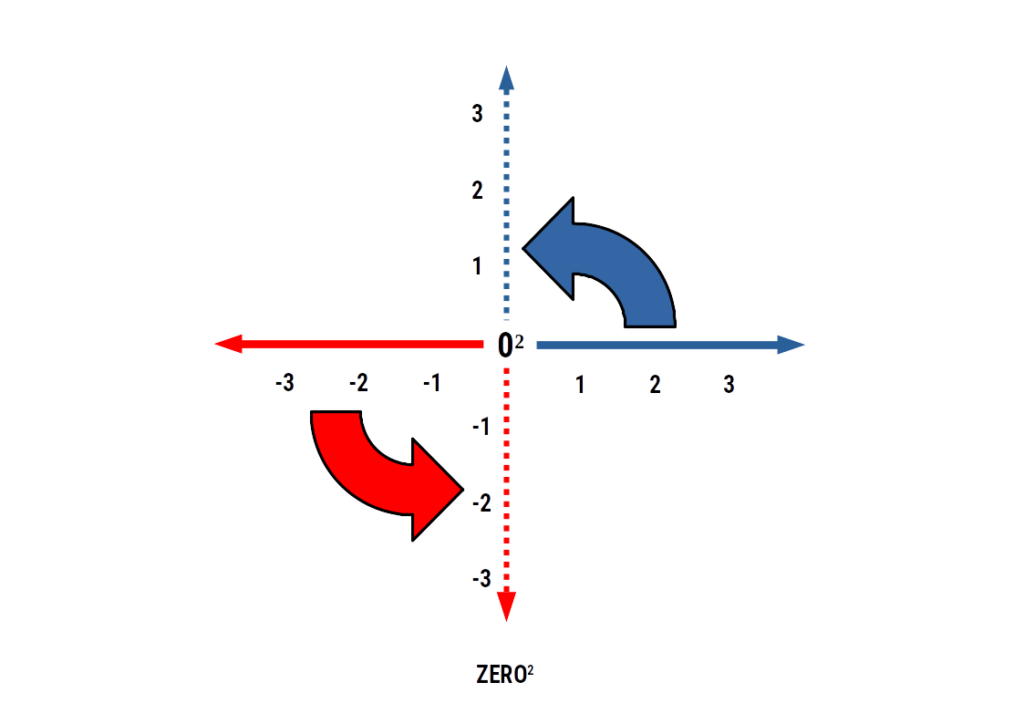
ZERO² is a geometric function that rotates the entire number line at 90° to the…
8 Infinities on the Number Line
There are 8 distinct infinite boundaries that appear on the number line. Two either side…
THE
Concept
Squaring the Number line
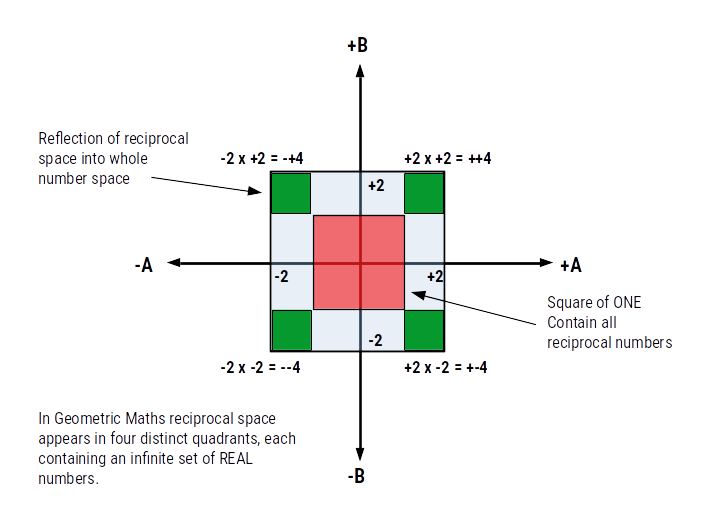
When zero is squared, it rotates a duplicate of the number line to rest at a 90° degree angle to the original. Each of these two number lines exhibits a negative and positive aspect that is equally divided by the zero at the centre of the cross. As there as two number lines, we can multiply any value in each quadrant and find a point located on the number plane. In this way, a negative that is multiplied by another negative will be found in the negative space, unlike traditional mathematics that places the result in the positive.
NOTICE: The bottom left of the diagram contains a space where the multiplication of two negative number (negative squaring), are found. In traditional mathematics these values are translated into the positive, top right square (blue).
This means there are an additional three number spaces that are only accounted for in geometric maths. The first arises from the multiplication of two negative numbers. However, a further two more arise from a positive value multiplied by a negative. This can occur in two ‘orientations’, negative first or positive first. In 4D and geometric maths, the order of a calculation does affect the outcome of the result. 3×2 is not the same as 2×3, even the result make look the same on a standard calculator.
Key point
In 4D and geometric maths the order of a calculation matters.
This is an important deviation between the traditional mathematical view. It is important to note that the results derived on a standard calculator are programmed to produce a particular answer. If instead of using the power function on a standard calculator we enter the values directly, we still find that the same result can not be achieved as the system of Geometric maths.
Traditional Squaring result
4D Maths Squaring result
NOTICE:the results of 4D mathematics include a total of four number spaces, compared to traditional mathematical axioms that only allow for two. This is due to the nature of deriving both numbers of the equation from a single number line, instead of two different number lines, as is the space on the 2D number cross.
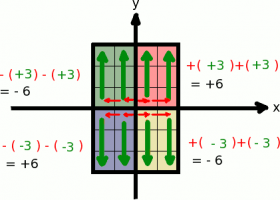
Simultaneous Calculations
One of the key differences in the system of Geometric maths is the capacity to produce simultaneous calculations for each quadrant of the number cross. The provides mathematical answers that can be expressed as a 2D geometric shape.
Here we can see the geometric nature of negative squaring, as we perform 4 simultaneous calculations of the number 2.
Axiomatic Basis
Whilst researching the nature of negative squaring, we were able to find a similar concept in an advanced form of calculus.
Normally in mathematics, a surface is always considered positive. However, we see that in order to achieve this, the two values must be added together. This in turn produces a different result to the concept of negative squaring.
So Why don’t negative squares exist?
The answer to this appear to be how traditional mathematics has been constructed, rather than an immutable principle of number theory.
Here is an example of one proposed reason from a fellow mathematician, however we can see that if a and b are constructed from the two different number lines of the number cross, then the ‘proof’ does not hold.
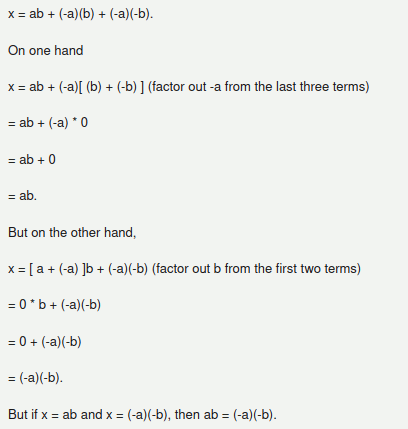
Feedback from other mathematician about our concept of negative squaring suggests that we are incorrectly assigning a polarity to length and width dimensions. Yet, geometric maths in not about assigning dimensional space. It is a numerical system, that exhibits a particular type of number plain, which can also extend into higher dimensional constructs.
feedback on our negative squaring concept from a friendly mathematician
Even more complicated ‘proofs’ such as the ‘ring of distributed numbers’, still rely on the notion that a and b, in an equation are derived from the same number line. Which is not the case in Geometric and 4D maths.
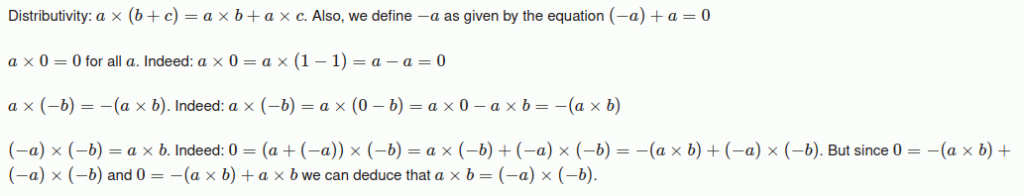
The concept of the ring of distribution of the real numbers presented from a friendly mathematician
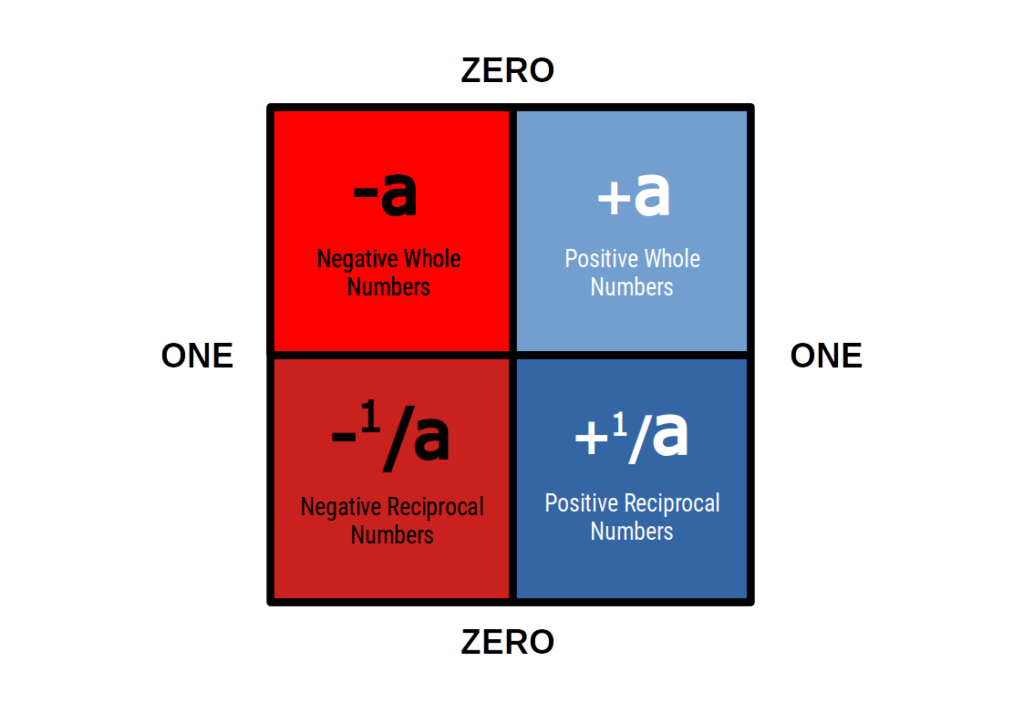
In the above we can see that (-a)+a=0, however there is no polarity assign to zero. In Geometric maths, zero comes in both positive, negative, and neutral forms. The ‘Real’ numbers are all contained within reciprocal number space that is reflected into whole number space. Whereas the above proof makes no differentiation between numbers such as 0.99999… on into infinity, and the number 1. Just when dealing with the true nature of the infinite, we utilise the nature of the boundariess formed by the squaring and rooting of reciprocal values.
THE
Conclusion
So what does this tell us the concept of squaring?
There is no mathematical reason for the exclusion of negative squaring from occurring. Moreover, it is a choice of perspective. The System of Geometric Maths explores the infinite nature of numbers that a formulated within the confines of reciprocal space first, and then subsequently reflected into whole number space.
What are the consequences of negative squaring?
Traditional mathematics has expressed a belief that ‘no new numbers exist beyond the concept of the complex plane’. Yet in Geometric Maths, we find that 3/4 of the number sets are missing from the linear interpretation of number space. Moreover, this leads to a different axiomatic belief that suggest two negative make a positive, which is not the case in 4D Mathematics. The shift in perspective formulated through a geometric appreciation of numerical space allows us to solve seemingly impossible paradoxes, such as those presented by the Continuum Hypothesis.
Carry On Learning
This article is part of our new theory, ‘Maths of Infinity‘
Read the main article or browse more interesting post from the list below
The Zero Boundary
The Zero Boundary divides the infinite sets of positive and negative numbers, and is defined by the process of division.
The Infinity of ONE
The Infinity of ONE is revealed by the nature of reiterated root calculations. This divides the number line into reciprocal and whole number space.
Reciprocal number space
All numbers beyond ONE have a reciprocal representation between the numbers ZERO and ONE. It is this mirror-like nature of
YOUR QUESTIONS ANSWERED
Got a Question? Then leave a comment below.
Question?
How can the multiplication of two negative numbers result in a positive?
ANSWER?
Actually results in a double negative, a notation not used in standard mathematics. However, as two negative do actually form a positive, you can also perceive the –n numbers in Geometric Maths as a kind of positive number space. As this numerical space is not within the make-up of traditional mathematical axioms, it has no expression.
Question?
Why do we need these four types of mathematical space, ++, – -, +-, -+. what use is that?
ANSWER?
There are plenty of real world examples where these 4 types of mathematical space are used. For example, Electromagnetic wave, D-orbitals in the electron cloud, are both composed on a cross at 90°. Furthermore, negative squaring is based on the concept of 0², which lays the foundation for the 0³ hexagonal number plain.
