Traditional mathematics sees numbers and mathematical operations from the perspective of a 1 dimensional number line. However, from a geometric perspective, numbers also occupy higher dimensional spaces. This idea when applied to the axioms of mathematics reveal a whole new dimension to numbers, and the possibility of producing calculations that have no form of expression in conventional theory.
Overview
We frequently take for granted the four mathematical operations—addition, subtraction, multiplication, and division—which constitute the foundation of all mathematical computations. However, if we look more closely, we can find certain numerical requirements that characterise eight different kinds of infinity on the number line.
They expand into two opposing infinite extremities and surround the borders of ZERO and ONE. Understanding this restriction helps us to have a deeper comprehension of the nature of the infinite, which begins to challenge many mathematical conventions of our present day.
THE
Concept
The Nature of Zero
Mathematics is founded upon the notion of 4 types of numerical operators; addition, subtraction, multiplication, and division. Each exhibits unique qualities that can help us comprehend the nature of infinity.
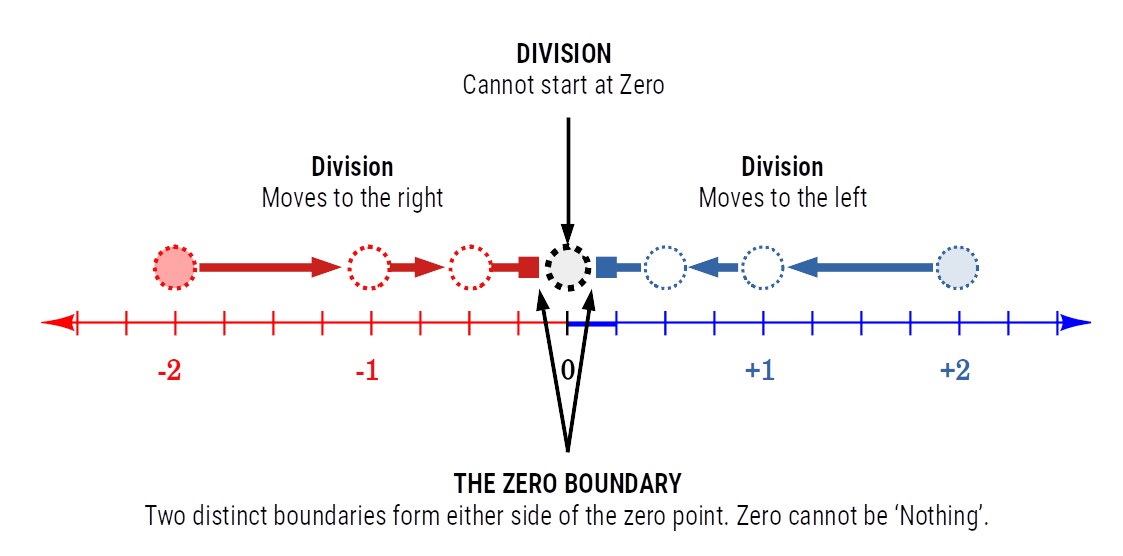
A whole number can be divided into infinitely smaller parts. The process can be reiterated, diminishing towards zero, yet the result will never cross the zero point. The same can be said for numbers in the negative.
As the two boundaries are distinguished from each other, then the zero that sits at the centre cannot be ‘nothing’. This demonstrates that the number zero exhibits an infinite boundary on both its positive and negative side.
FIND OUT MORE ABOUT THE ZERO BOUNDARY
Did you ever question?
Why are there only 4 mathematical operators?
Can cross the Zero point
Can NOT cross the Zero point
Equal Values
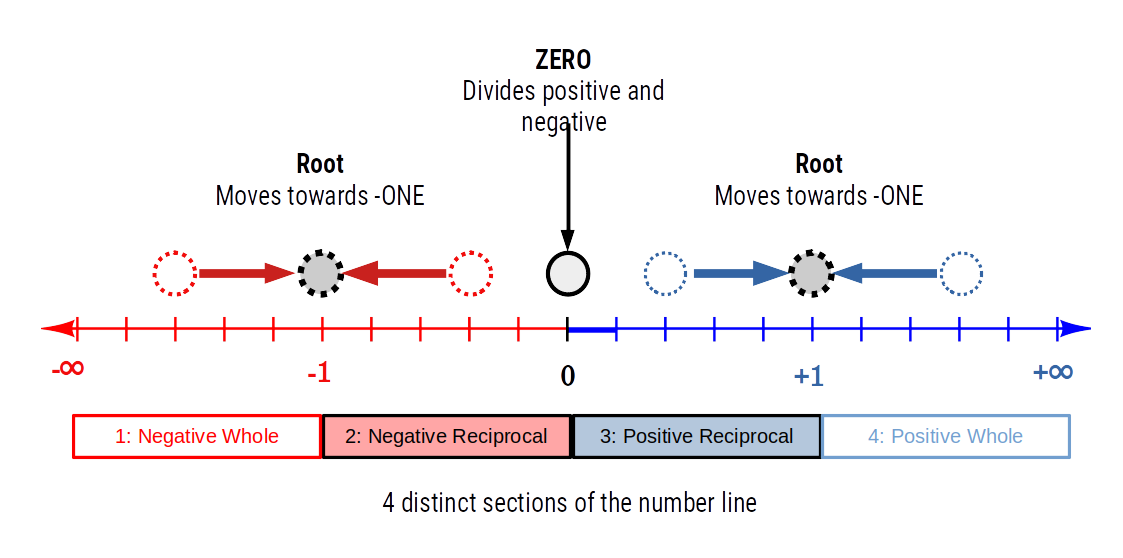
When values of the same quantities are operated upon, we notice the situation changes. Addition now doubles the quantity, whereas subtraction dissolves it back to zero. When we multiply or divide equal quantities we call it the square, or root of the number.
If the squaring or rooting function is reiterated to an infinite degree, and the initial value resides between zero and one, then the result will tend to move either toward zero, in the case of squaring, or toward the number one, when the root value is found.
Yet, no matter how many times the calculation is reiterated, the result will never be able to cross the boundary of ONE.
FIND OUT MORE ABOUT THE INFINITY OF ONE
Try It for Yourself!
1: Take a simple calculator and press the number 2.
2: Find the square root button (√), and press it: the result is 1.414... or √2.
3: Keep Pressing the same square root button over and over again.
Notice that the answer never goes below ZERO.
NOTE: If your calculator does go to zero, that is because it has run out of memory. Infinity is beyond the ability for a machine to calculate
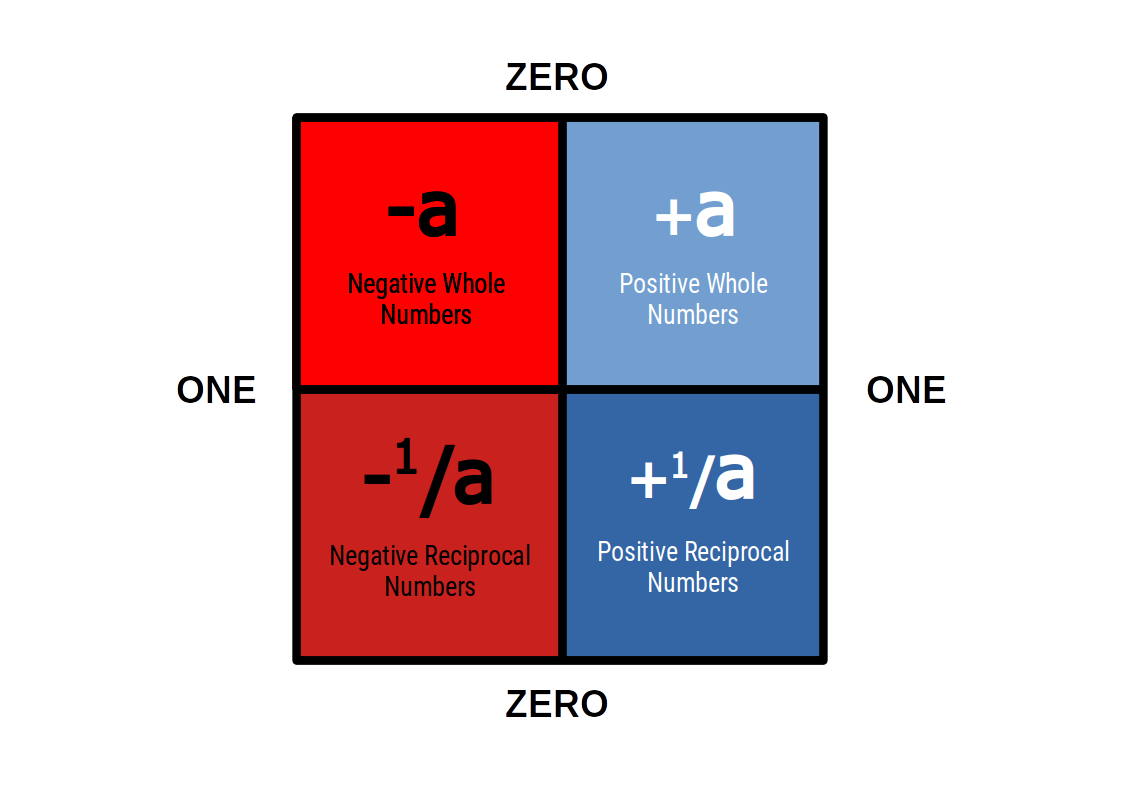
Reciprocal Number Space
The reciprocal number space between ZERO and ONE contains all the possible whole numbers. Except ONE and ZERO, all numbers, even primes, can be divided by one to find its reciprocal fraction. We call this space between zero and one ‘Reciprocal Number Space’.
FIND OUT MORE ABOUT RECIPROCAL NUMBER SPACE
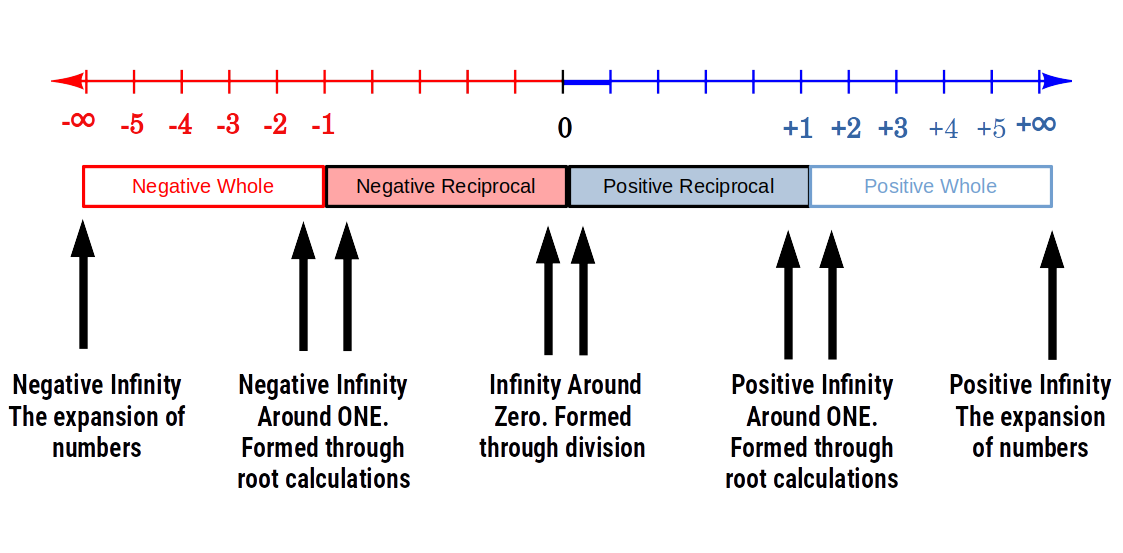
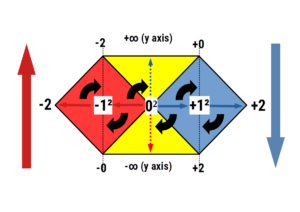
8 Infinities on the Number Line
By identifying the limitations of the number zero and one in reciprocal space, we are able to make an examination of infinity as found on the traditional number line.
By performing squaring or root calculations for any whole number, we find that multiplication expands into infinity, whereas a root function will diminish towards ONE. Here we see that, similar to the number ZERO, the number ONE exhibits two boundaries, one on the whole number side, and one on the reciprocal.
Generally, we can see that negative numbers should perform in the same way as positive integers. However, due to the established axioms of current mathematics, two negative numbers will make a positive square. However, in Geometric Maths, this issue is resolved by a cleaner definition of the concept of powers, and negative powers.
Is it just a coincidence that the number 8 and the infinity sign should share the same symbol, rotated at 90° to each other?
Once we resolve the ‘negative square root’ issue, then we can define an additional set of boundaries around the number negative ONE. This is a key step that has been missing from modern mathematics.
If we include the two infinite series of positive and negative whole numbers, which expand into infinity, we have correctly identified the 8 types of infinity that can be found on the number line.
FIND OUT MORE ABOUT THE 8 INFINITIES ON THE NUMBER LINE
Reciprocal Prime Numbers
As Reciprocal Space contains all prime numbers, we can conclude that the number 0 and 1 are particular precursors to all other numbers, including primes.
In the consideration of reciprocal prime numbers, we find that numerical space is divided into smaller parts as we progress through the infinite set. If a number create a division that falls over the same place as the one that precedes it, then the number is not a prime.
Based on this logic, we can see that we should be able to take the closest point of division and be able to predict the series of prime numbers.
Unfortunately, this in not the case.
Why are prime numbers so unpredictable?
Due to numerical powers, and in particular the nature of the number 37, all prime number predictions begin to fail. However, what this highlights is that the number line is not an accurate depiction of numerical space.
FIND OUT MORE ABOUT RECIPROCAL PRIME NUMBERS
Beyond the number ¡
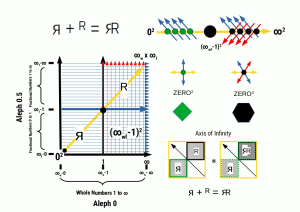
The traditional expansion of numerical space is termed the complex plane. The number ‘i’ was developed to compensate for the inability for the traditional number line to accommodate -√1. However, our new mathematical observations begin to allude to the fact that both square and root numbers, whether positive or negative, express a particular quality in relation to the number ONE and Infinity.
As the number ‘i’ only accounts for the -√1, it is not adequate to express this infinite relationship for other root or square numbers. The picture that begins to emerge is that the number ‘i’ is only one of a whole set of root and square numbers, that have yet to be accounted for.
There's more to maths than meets the ¡
The significance of this is that it provides a new mathematical solution to the Continuum Hypothesis, that lies right at the heart of mathematical debate around the topic of infinity.
FIND OUT MORE ABOUT THE NUMBER i
THE
Conclusion
The GEOMETRIC MATHS examines numerical space primarily in terms of a MULTI dimension number line.
In this introduction what we have shown is that:
- Zero is not ‘nothing’.
- Division creates the boundary around the number ZERO.
- Square and Root function that operate on reciprocal number space can never exceed the boundaries of ZERO and ONE.
- There are 8 types of infinity that are found on the number line.
- By examining prime number reciprocal space, we can ascertain that the number line and number i are missing expressions such as √2, √3, etc. despite appearances.
Carry on Learning
This post form part of our new theory of Geometric Maths by browsing the post below.
What is the continuum hypothesis?
The Continuum Hypothesis was the #1 mathematical challenge set by Hilbert at the start of the 1900’s. It was only ever solved in the negative.
The Riemann Hypothesis: A Geometric Solution
The Riemann Hypothesis is the number one mathematical challenge of today. We offer a geometric solution to the problem, that confirms all non-trivial zero will appear on the critical strip.
Solving Infinity
By assessing the nature of numbers, base systems, and solving infinity, we lay the foundations for a solution to the Russel paradox, and Continuum Hypothesis, and much more.
'SOLVING THE INFINITE'
In2infinity's new solution
to the Continuum Hypothesis.
Listed as the most important mathematical challenge of the 1900s, In2infinity sheds new light on the answer, disproving the present solution, and opening the doors for a whole new math of infinity.
Explore our theory
Geometric Maths is JUST A SMALL part of our new theory
FIND OUT MORE BY about our new perspective of number
4D Maths
4D Maths is a fundamental step into a new dimension of mathematics. Founded upon the idea of space, time and dimension, and the infinity equation, 0 ±1= ±∞, the 4D calculator generates new insight into the infinite nature of numbers, and introduces the ‘Theory of Effort’. Overview How numbers are created 4D Maths suggest a new type of categorisation of
