The nature of infinity has plagued mathematics since time immemorial. An enigma that is found at the end of all numbers, and yet is also contained within a single unit space. These paradoxes have never been overcome. However, our new geometric mathematical theory sheds new light on this nature of infinity, providing a fresh new perspective that can overcomes our current mathematical limitations.
Overview
The nature of infinity has plagued mathematics since time immemorial. As well as appearing at the periphery of the number line, it also appears within a single unit measure. Traditionally, mathematics has always considered numbers to exist on a single line, with the complex plane considered to be the end of all number types. In our new Geometric mathematical theory, we propose that this is not the case. Based on the principles of Euclidean Geometry, extended into higher dimensions, Our new theory of Geometric Maths, can Rotate, and translate, and fold number space, providing us with a fresh perspective of the nature of the infinite.
KEy Points
-
A new mathematical theory that can transform number space and provide new insight into the nature of infinity.
-
Based on the principles of Euclidean Geometry, extended into higher dimensions
-
Provides solutions for the Continuum and Riemann hypothesis.
Check out these Solutions to the Infinite
Our New concept of Geometric Maths provides solutions to the greatest unsolved challenges in mathematics
The Riemann Hypothesis: A Geometric Solution
The Riemann Hypothesis is the number one mathematical challenge of today. We offer a geometric…
Aleph 05
Adding sequential fractions creates a series that expands by 0.5, forming an infinite set between…
What is the continuum hypothesis?
The Continuum Hypothesis was the #1 mathematical challenge set by Hilbert at the start of…
THE
Concept
The challenge of Infinity
You may think that one of the most simple things we can do is count. Right from before we could even walk, we were exploring the mental faculty. Yet George Cantor in his diagonal proof demonstrated that it is impossible to list them all. We simply cannot count ‘ALL’ the numbers without creating another set of infinite number that move across the diagonal, which would create a repeat number. And that is just the whole numbers. The situation gets even more complex when we add in the reals. Decimal fractions can also be expressed in an infinite variety. If we can’t list the infinite set of whole numbers (ℵ0), then how can we list the reals (ℵ1)?
George Cantor was able to prove that ℵ1 was denser than ℵ0, but could not determine by how much. The Continuum Hypothesis arises as a result of trying to answer this question, which lies as the heart of the number theory and philosophy.
The size of infinity
The first problem comes from the fact that it seems impossible for us to measure the ‘size’ of infinity. What we can say is that if an infinite set is missing some numbers, then it has less density than another infinite set. Through bijection, we can establish this relationship, which is how we can tell that ℵ1 has a greater density than ℵ0. Simply put, there are more decimal fractions than infinite whole numbers.
As infinity is often presented as a boundless entity, the only tools for qualifying have been through projecting the outcome of a relationship into infinity. However, without knowing the size, how can we say how much bigger one type of infinity is from the next. What we need is a new way of perceiving mathematics that will allow us to qualify ℵ1 and ℵ0 and any other type of infinity. If we can find an infinite set that exists between them, then the continuum hypothesis will be solved.
There are more decimal fractions than whole numbers.
Law of equivalence
The Law of equivalence is traditionally derived from Chemistry. When two substances are mixed, then a chemical reaction takes place. Once the reaction has completed, the substance will be equal throughout.
In our mathematical system, the Law of Equivalence is derived from the axiom from Euclid.
(7) Things which are halves of the same things are equal to one another
If you half infinity we get two equivalent infinities. The first example of this on the number line are the infinite set of positive and negative numbers. Yet there still remains one number at the centre. ZERO. A positive and negative infinity.
Infinity divides into two creates two infinities that are equivalent
FIND OUT MORE ABOUT THE LAW OF EQUIVALECE
Non-Polar Numbers
Zero has been a slightly tricky number in terms of mathematics. Often whether is included in the set of whole numbers is a matter of personal preference. Yet at first appearance is does not seem to offer any kind of polarity, like all other numbers. To complicate things, zero does not play well with mathematics. whenever we perform a calculation with zero the result seem to be zero. That is the problem with non-polarity. The maths don’t work.
In order for us to complete the set of ℵ0, we would like to add another number that seems to have been missed out.
Zero+ and zero- are not commonly given their rightful place in the classification of number. Yet all numbers in the reciprocal space between zero and one begin with the number +0.xxx… The same can be said of the negative numbers indicated by -0.xxx…
With the addition of the +0 and negative zero the number range from:
-∞←-3,-2,-1,-0, 0, +0, +1,+2, +3→+∞
Due to its non-polarity, we can optionally remove the zero (red) so that positive and negative number space now form a one-to-one bijection. This means we can focus on just one side of the number line, as any result will be the same when considering the complete infinite set of both positive and negative number.
Let us clarify that the definition of ℵ0 are the whole numbers from zero to infinity.
0, 1, 2, 3, → ∞ = ℵ0
Any other number, outside of the complex plain and the non-polar zero, is considered as a part of ℵ1. i.e all decimal fractions that are not a part of ℵ0 .
As the categorisation of ℵ0 and ℵ1 provides the framework for the continuum hypothesis, we will try to remain within the bounds of the challenge that has been set.
For those unsatisfied with the removal of the non-polar ZERO, you will need to explore our broader solution to the Infinite. This offers a completely different categorisation of number, which is based on the evolution of mathematics from the process of dividing infinity. This places ZERO, ONE, & TWO in specific categories, which enable us to overcome the Russel Paradox.
FIND OUT MORE ABOUT THE ZERO BOUNDARY
Uncountability
As George Cantor with his ingenuous diagonal proof showed that you cannot list all the numbers. But does that mean you cannot count them? When we make a list we are creating a record, but when we count we are performing a calculation.
In its simplest of terms, counting sequential numbers, starts at zero, to which we add one. The process just repeats on a loop into infinite, as we generate the entire set of sequential numbers. Performing a calculation, is different from writing down the answer. The answer occurs once the calculation has been completed.
In the case of infinity, there are plenty of example of algebraic numbers that exhibit an infinite fraction. √2 for example. We know how it is constructed, but we have never been able to produce the number, as it is an infinite decimal fraction. So in this sense we can never list any number. We can only calculate it to a certain degree.
Number systems
So the first challenge is to understand the nature of counting in more detail. Going back to the basics, we normally write our number system in base 10. We can also use other bases, but for now let’s use this as it’s the most familiar. When we formulate a number, a base system creates a grid of a specific dimension.
Due to the way that most people have been taught to count, the number grid upon which most of us perform our calculation looks like this.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |
| 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 |
| 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
Remember Zero
This base 10 number grid is shown to us when we first begin to learn about multiplication. In the x direction (→) the numbers repeat 1 through to 9 and then flips to a double-digit number 10. This has a zero in its second position. In the y direction, the numbers begin with 1 and the next number set runs from 1 to 10.
Looking at this table, we can see that the symmetry is off. We can begin to remedy this by adding a zero to the top row. Now the numbers run from 01 to 10 in the x direction. However, we have forgotten one thing; ZERO at the start of the number line.
| 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |
| 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 |
| 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
Number Order
To complete our defined set for ℵ0, we need to include the number zero. Once placed at the start of the numbers we find that all the number suddenly line up. The first digits process in the x and y direction from 0-9, which is correct for our definition of ℵ0.
This symmetry is nice, as the 10 times table runs through the y-axis, the 11 times table runs through the diagonal from 00 to 99, and the 9 times table appear on the second diagonal.
The 1x table runs through the sequential rows, which is the simplest to calculate, and creates the sequence of number that is then structured into a mathematical order using a base system. We employ this system, to calculate and make sense of the infinite variety of number available to us. It’s all about the order on a 2D plane.
However, there is one small problem. As the numbers get bigger, so we need more and more digits to accommodate their place within the sequential numbers. The grid of 100 squares only contains 99 of the numbers. The number 100 instead begins a new row, introducing triple digits for the first time.
| 00 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 |
| 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 |
| 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 |
| 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 |
| 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 |
| 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 |
| 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 |
| 100 |
In truth, if we look at the other diagonal lines, we see that any square at a diagonal to another with either add or subtract 9 or 11 from is total. Multiplication occurs as a specific form of addition that is only express on the diagonal of the base 10 number grid.
Zero Placeholder
As the sequential numbers progress, so we appear to need to add more and more zeros to the number in order to distinguish it from the other numbers.
In the first row we have the single digit numbers. Then the next nine rows comprise the double-digit numbers. As we add a third digit, the number of possibilities increases dramatically. This logarithmic pattern expands at different rates, depending on the base system used.
The expansion of a number is as a direct result of zero as a placeholder for larger numbers. We add zero to the end of the number and then start over, changing each unit at each step.
| 0000 | 0001 | → | 0009 |
| 0010 | 0011 | → | 0099 |
| 0100 | 0101 | → | 0999 |
| 1000 | 1001 | → | 9999 |
Yet, if we look at the first line, we added a zero in front of the single digits numbers to bring them into symmetry with the other numbers. The number 01, 001, or even 0001, are just extensions of this concept. Each zero added in front of a number brings it into context with the next larger set. With four digits, the number run from 0000 to 9999, and so on into infinity. Therefore, there are an infinite number of zeroes preceding the number 1, or any other number for that matter. We just forget about them for convenience.
Infinite numbers
The key to counting is our ability to extrapolate information from the infinite. We don’t use the number 001 each time we formulate a calculation. We can happily remove the surplus zeros, without much of an issue. However, when dealing with infinite sets, we cannot afford such a luxury. We must see the infinite, even if we cannot write it down.
Logic tells us that if numbers are infinite, so are the number of digits needed to express it. Yet, the number one appears to us as a single digit. We can see this is also not true, as 01, and 001 are also valid expressions. So what about an infinite number of zeros. Why should we be limited to placing just a few zeros in front of a number, especially when considering the infinite.
By placing an infinite number of zeros in front of the prescribed number, the number grid takes on a different quality. One that allows us to explore the infinite side of numbers
| ∞0→0 | ∞0→1 | → | ∞0→9 |
| ∞0→10 | ∞0→11 | → | ∞0→99 |
| ∞0→100 | ∞0→101 | → | ∞0→999 |
| ∞0→1000 | ∞0→1001 | → | ∞0→9999 |
In the example above, the expression ∞0 represents an infinite number of zeros, appended to the number. The remainder after the arrow is the part that differs from the rest of the infinite set.
Notice on the right-hand side, another pattern is emerging. The numbers are all composed of the number nine. This is because in base 10, 9 is the last number. However, if we follow the logic of what is presented, we find that all numbers will form an infinite set of nines at the point of infinity.
∞→99999→∞
This result is a consequence of base 10. If we employ another base system then the numbers at the end will differ. So if we are to uncover the mystery of infinity, we need to find a way to overcome this limitation.
Base Infinity
Base numbers systems can be considered the de facto methodology by which numerical space is ordered. A base system defines the number of symbols available to us for this construction.
Different base systems are in operation throughout our daily lives. Time is metered in base 12. The number 12 being also zero at midnight, for example. Computers use binary, and hexadecimal byte systems in everyday operations. Each base system uses the same mathematics and numbers but expresses it using a particular set of symbols.
The most simple system is binary code. A simple on/off, zero/one, mechanism of number that is needed to process any kind of calculation. This is called base 2. A base 1 number system would only be able to express one digit, and therefore can only display the number zero.
Beyond base 2 there are larger base number systems. We use base 10 in everyday calculations. The Sumerians used a base 60 system for their calendars. When considering infinity, we should also ask, “How many base systems are there?”
The answer is there are an infinite number of base systems. Even if base 1 does not produce a mathematical process, it does create an infinite set of zeros, so can be included in the list.
base 1 = 00000000
base 2 = 010100101
Base 3 = 012020121
Base systems determine the number of possibilities a single digit may take. As we move up in base number, so the number of options available to us increases towards infinity.
By way of example, we take a pen and make a set of random markings. We can do this indefinitely, creating an original piece each time, and order them is a sequence to form a number line. Similar examples are found in nature. Take two leaves from a tree and compare them. No matter what, you will always find a slight difference between them, even though their characteristic might match.
The same goes for numbers. Each one is identified by its symbol. At base infinity, this could be anything ‘number’ from the infinite line of already existing numbers. Therefore, we can express base infinity as a line of infinite infinities.
base ∞ = ∞…∞∞∞…∞
Wholes and Fractions
In base ∞ numbers get a little bit tricky. However, there is another part to numbers that can help us make more sense of them. The decimal fraction.
In truth, all numbers can be expressed as a decimal fraction. In the case of whole numbers, the fraction is denoted by an infinite number of zeros. Just as we omit the zeros as the beginning of any number, so the same can be said of the zeros appended to the fractional part of a whole number.
When viewed with its infinite fraction expressed, we get the following
0 = ∞→…000.000→…∞
1 = ∞→…001.000→…∞
2 = ∞→…002.000→…∞
The decimal point divides whole a fractional space like zero divides positive and negative number space.
Therefore whole numbers can be defined as a number that exhibits an infinite number of zeros after itself, even if we are using base infinity.
A whole number iN base infinity
∞→…∞∞∞.000→…∞
If we inverse this presentation and place the infinite set of zeros on the left, and the infinite set of infinities on the right we get the infinite set of reciprocal numbers between zero and one.
A Reciprocal numbers in base infinity
∞→…000.∞∞∞→…∞
In our new system of mathematics we categorize reciprocal numbers as a different class to the rest, thus overcoming the russel paradox
The decimal point
When viewed through their consistent decimal format, we can see that numbers are formed from two sets of infinite, the whole parts and the fraction. These two infinities are separated by a decimal point. This mathematical notation resembles a dot. Just like the non-polar ZERO that sits at the centre of the infinite negative and positive number sets, the decimal point holds no identifying characteristic. In fact, the similarities from the perspective of infinity are quite profound. If we include the negative numbers for a moment, then the pattern becomes quite clear.
∞…← -1.0 | -0.0 | 0 | +0.0 | +1.0 →…∞
The decimal point divides whole a fractional space like zero divides positive and negative number space.
In this example we only show whole numbers, and have omitted the infinite zeros from in front and behind each integer.
Viewed like this, we can see that zero divides positive and negative number space in the same way that the decimal point divides whole and fraction part of any number.
Using the process of bijection, we can understand that the positive and negative portions of the number line are in one-to-one correspondence. This also follows the law of Equivalence as infinity is divided into two parts, so both are equal.
The same can be said of each infinity that exists either side of the decimal point. Whatever can be created on one side can also be created on the other. As whole numbers are the foundation for ℵ0 and fractions the basis for ℵ1, with these observations we can begin to form the final picture that will answer the continuum hypothesis.
Uniqueness
When expressed in base infinity, each unit of a number has a unique expression, which completely differentiates it from all others.
In base infinity, this uniqueness is expressed as a single digit, which by its nature will be different to all others. In this way, we can ‘collapse’ the whole list of the infinite whole numbers into a single infinity.
Infinite potential
∞ ∞ ∞ →…∞
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
Unique expression
+1 +1 +1 →…∞ = ∞
Once a number is ‘written’ (listed) is forms a unique expression, so we no longer need any ‘digits’ to represent it.
Similar to the scientific notion of observation. A number written down is an observable phenomenon. We can write any kind of symbol or glyph and attribute it to any number in existence. But once it is used to represent a particular quantity, it must be removed from the infinite set. As we add together each unique number into infinity, so we are adding an infinite series of +1, which is exactly how the infinite number series is formed.
0 +1 = 1
1 +1 = 2
2 +1 = 3
But adding 1 at each stage the infinite set of sequential whole numbers is produced. This notion lies at the heart of the mathematics of infinity and the infinity equation, which states:
0 ±1 = ±∞
This is a recursive calculation, that at each step generates the next whole number. Numbers are not written, they are calculated.
Whilst simple in nature, this equation has deep implications. If reiterated into infinity, the result should ultimately reach one end of the whole number line, depending on the ratio of +1’s to -1’s. However, in reality it significance it much deeper. For it suggests that the infinite set of whole numbers is derived from the notion of ±1, as whatever number we can imagine there is always one less or one greater.
Key point
Any whole number above one is calculated
Solving the Infinite
With the knowledge we have explored thus far, we can now begin to construct the framework that will answer the problems posed by the Continuum Hypothesis.
Through our observation that in base infinity the whole number set ‘collapses’ into a single in infinity, we have avoided the pitfalls of the listed number set. Instead, we have proven the uncountability of number through the observation of how we are extrapolating from an infinite set only those digits that form a particular number. As an infinite set can be represented as a single unique digit, we avoid the diagonal argument completely, and at the same time collapse the infinite series into a single infinity.
As we know that the fractional side of a whole number must be equal to an infinite set of zeroes, we can ascertain that:
ℵ0 = ∞
The solution to ℵ0 is determined through observations in base ∞
The reason we know that the two infinities, whole and fractional, are equivalent, is because they exhibit a one-to-one correspondence. We can therefore ‘collapse’ the fractional side into a single infinity, just as we did with the whole. The result is infinity followed by a decimal fraction that is also denoted by infinity:
∞.∞
Infinite Proportions
The order of things is a very important concept, especially when dealing with infinity. Just as a computer needs to execute lines of code in a certain order, to run a program, so the same can be said in the world of mathematics, even when dealing with infinity.
When we consider decimal fractions, the number before the decimal point represents a whole number. We have ascertained that the value combines into a single infinity, ℵ0=∞.
On the other hand, each unit has an infinite number of variations that can appear on the fractional side. If we begin to count through the whole numbers, we therefore find that each whole number is accompanied by an infinite potential of a fraction :
0.∞, 1.∞, 3.∞ →∞
If for every whole number there is an infinite fraction then the ratio between the two parts should be:
1:∞
It follows then that if ℵ0=∞ then ℵ1=∞².
ℵ0=∞ then ℵ1=∞²
ℵ0 has a proportional relationship to ℵ1 that is a square power. ∞² is more clearly defined in our concept of 4D squaring.
As far as we are aware, this is the first definition that mathematics has for these two identities. Having established the ratio of the two, we now have all the elements in place to finally solve the continuum hypothesis.
Overcoming the paradox
As ℵ1 has an infinite possible representation with every unit of ℵ0, we might think it’s safe to assume that the continuum hypothesis should be solved. If infinities are always equivalent and equal, it is only by the order of their appearance that a difference can be found.
In fact, it is the difference between the whole and fractional infinities where the logical construct proposed so far come crashing down.
This problem lies at the heart of the Russel Paradox, which picks up on a small but highly significant point. All numbers above one have a reciprocal value between the numerical space of 0 and 1. This includes all whole numbers from 2 upwards. The number 1 does not have a reciprocal value.
If we decided in to exclude zero from ℵ0, then the space between 0 and 1 would not have been included. As we cannot create any reciprocal
From this we can see the paradox. If the whole numbers appear in the space between one and zero (as reciprocals), and the other spaces between 1 and 2 for example, do not, then surly there should more numbers in reciprocal space then in the other number spaces?
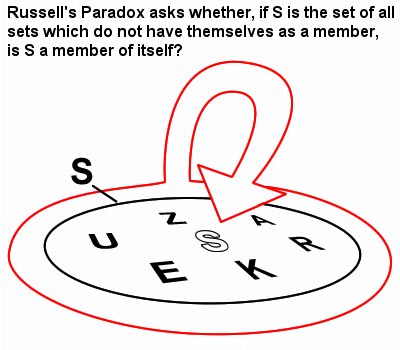
On the other hand, we have just asserted that ℵ1 = ∞² based on the idea that all infinities for each integer are equal. So which is true?
This conundrum has baffled mathematicians, and It’s easy to see why. For if we approach infinity at the wrong angle it is very easy to get lost in logical loophole like these.
However, as we have overcome the ‘counting’ issue through a completely new methodology, we are in good stead to tackle this paradox through our logic and reasoning.
Reciprocal space
The result of our enquiry has led us to state that ∞.∞ is the basis for the relationship ship between ℵ0 and ℵ1. Each infinite set is equivalent at this stage. We have included zero in both sets, which means we have the identity 0.0 in the set.
When the fraction part of the number comprises only zeroes, we know it is a whole number. Whereas, when the whole part consists of only zeroes, we know the number is a reciprocal.
Here we have the two type of number, whole and reciprocal, represented by the same qualities exhibited by both infinite sets (ℵ0 and ℵ1) that are also equivalent. As the reciprocal numbers lie at the heart of providing a solution to the Russel Paradox, we should investigate this occurrence in more detail and see what it reveals

To begin, we can examine the fractional side. As the occurrence of whole numbers appears only when the fractional number is equal to zero, we need to remove one unit from the infinite series for each whole number. The ratio established thus far between whole and fractional infinite sets is 1:∞. We only need to subtract 1 from the fractional side to account for the number zero, which forms each whole number. This gives us the ratio
1:∞-1
Next if we examine the whole number part of the infinite set, we find that whenever it equals zero a reciprocal number is created. As reciprocal values equal one out of the infinite set of wholes, we also need to subtract one from this side too.
∞-1 : ∞-1²
Notice the as the there are an infinite number of ‘fractions between each number space, the fractional set is squared. Remember this is due to the order of appearance, not the magnitude of infinite which remains in equilibrium at all times.
This means we have three types of numbers category. Whole numbers, Reciprocals and Fractions greater than ONE.
The Final Solution
The power of infinity
With this, we have all the ingredients needed to formulate the solution to the continuum hypothesis. Let us compare the identities of the types of number set. Fractional, Whole, and Reciprocal.
Whole ∞-1
Fractional (∞-1)²
Reciprocal (∞-1) x (∞²-1)
What we see is that the reciprocal values contain both Whole and Fractional infinite sets. This give the reciprocal set an identity of:
Reciprocal ∞-1³
With these identities establish we can make a comparison between all three:
Whole ∞-1
Fractional (∞-1)²
Reciprocal (∞-1)³
What we notice is that each set appears with the same identity that is increasing through powers. In our new theory of geometric maths, we claim that powers are functions, not numbers. Furthermore, root and power are responsible for the transformation of dimension, from a 1 dimensional line into the second dimension, and then 3rd and so on.
The conclusion is that numerical space is not a 1 dimensional edifice. Therefore, trying to classify numbers without consideration of the geometry of the number line is an impossibility. This becomes clearer when we explore the nature of numbers from a higher dimensional space than a line.
Number Geometry
It is generally agreed that x² demonstrates the formation of a square, and that x³ that of a cube. Euclid clearly stated that “The edges of a surface are lines.”, which has never been show not to be true, (except by non-euclidean geometry that bends space). As there is no need for us to complicate the issue of the infinite any further, our Geometric Maths is based in Euclidean Geometry. (We also have proofs that expose certain inaccurate postulates of non-Euclidean geometry).
Based on these geometric laws, we can finally construct a more accurate picture of number space.
Firstly, let us consider the relationship of the whole numbers to the fractional set. Whereas the wholes contain one infinity, the fractional set is squared. We represent this quite simply by producing a 2nd the axis at 90° to the first. We can label one axis Whole and the other axis Fractional.
If we remember, the reciprocal values between ZERO and ONE are missing from the set, as they comprise reciprocal space. Therefore, we can mark out this space to get the final result.
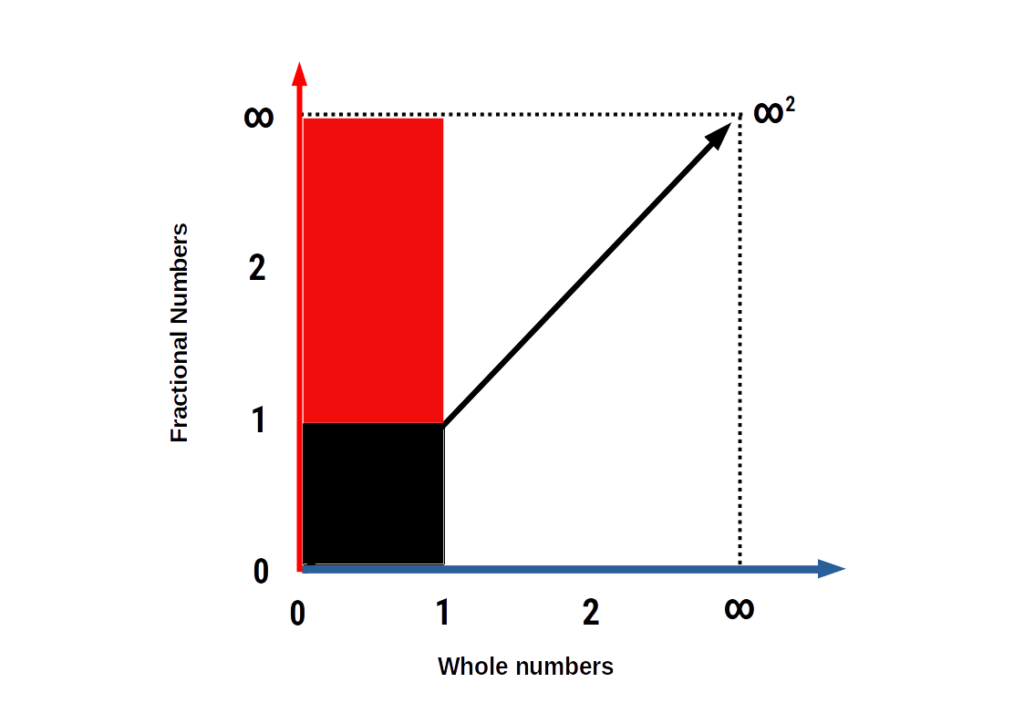
The red space contains the infinite set of fractions above one. As all numbers between 0 and 1 are reciprocal, all fractional numbers are contained within that set. However, as the numbers above 1 are all fractional numbers, the whole number plane is expressed only as a 1 dimensional line.
For those interested in the field of mathematics, might begin to see from this image how we are able to provide a very simple solutions to the Riemann Hypothesis, the next biggest challenge on the list of mathematical problems.
3d number space
With the 2D infinite number plain established, we now need to accommodate the reciprocal numbers. These contain both, all whole numbers and all fractions above one. Looking at the derived identity for the reciprocal we see that they are raised to the power of 3.
Again we add another axis at 90° to the square plain, to form an x, y, z co-ordinate. What emerges is a cube with a specific portion removed.
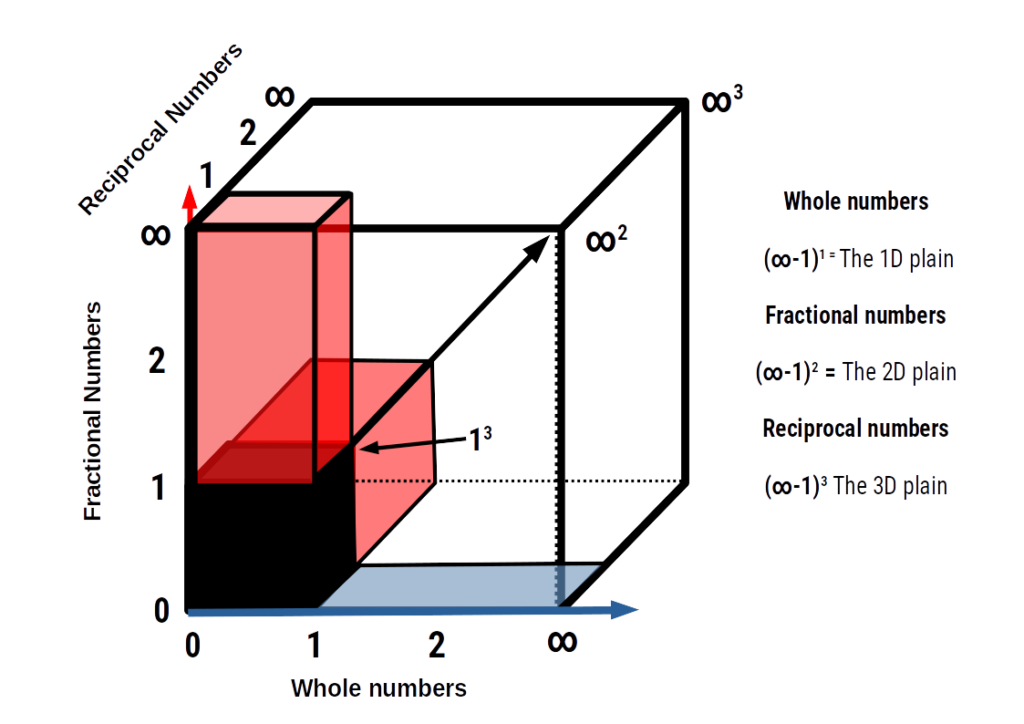
We should point out that the three types of infinite number set are exhibited in a particular dimension of space. A line is not just the side of a 2D shape. It is the 2D plane viewed side on which is rotated in 3D space. The 2D plain itself composed of an infinite set of lines, projected in the y-direction. At any point on the surface of the square, we find the interaction of two lines orientated at 90°. Therefore, any point on the surface represents a combination of two infinite sets. In this case, whole numbers form the line, and the surface of the square is generated by the infinite fraction.
Similarly, it is the volume of the cube that contains all reciprocal values, as a combination of both whole and fractional numbers into one infinity. This is not the line or the surface of the cube, but the volume of the cube. Just as we can take any point within the square, so the same can be said of the cube. This time, we see that each ‘number point’ is a composition of the three types of infinite sets. It is the combination of all three within the 3d dimension that allows for the number to have mathematical context. Each type of infinite can be expressed on the number line, just as 1, 1², and 1³ will all appear in the same place, yet are total different from each other. Only by looking at the problem from a higher dimensional space can we see the whole picture.
4D number space
The model of the infinite number cube has a few peculiarities that are worth further investigation.
Firstly, we notice that in 3D space, the number line is transformed into a 2d plane. The blue rectangle at the bottom represents the reciprocal values whereas the rest of the surface comprised of the fractional values. In the cube this is juxtaposed against the surface of the fractional and whole number sets. The nature of the number one creates a specific boundary we call the Infinity of ONE. This becomes easier to identify if we place these boundaries inside the cube.
The volume of a cube is a mathematically determined quantity, we can specify the dimensions, of the bottom cube of 1, which hold the reciprocal characteristics of all numbers. All whole and fractional numbers exist in the space above one, which occupies the cubic space in the far top right corner. As we know that reciprocal space has a one-to-one correspondence to the combined set of whole and fractional numbers above one, we can ascertain they must be of the same density, or size. Therefore, if the size of reciprocal space is 1³, then the same should be true of the size of the cube that contains all whole and fraction numbers combined. This produces 2 cubes that appear at opposite conners of the cube.
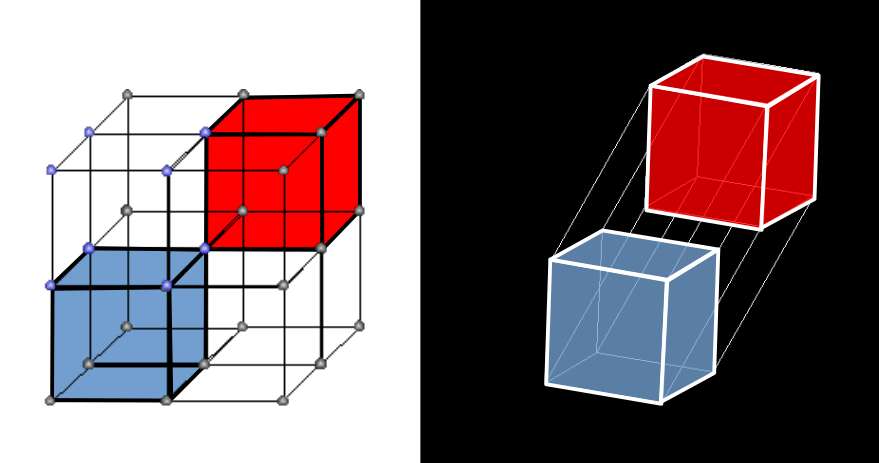
Left: fractional and whole number plane divides the cube of numbers into sections, of reciprocal and non-reciprocal numbers.
Right: the 2 cubes represents a 4D hypercube
The result is that we have generated a numerical model of numbers, which appropriates the form of a 4D hypercube. When rotated on its w-axis, the two cube swap places. Similarly, the entire set of decimals above ONE, found in the space of the red cube, is extracted from the reciprocal number space (blue cube) between zero and one.
The 4D Perspective
What we have revealed thus far is only an eighth of the whole picture presented by Geometric Maths. The 4th Dimensional Number Cube exhibits 8 types of reciprocal space compared to our traditional notion of numbers. Each of these is ‘reflected into eight whole number corner cubes. Each of these is of the same spacial dimension,

This idea of 4th Dimensional Number space is expressed in 2D with our concept of Inverse Geometry, and Rotational Squaring, that introduces the concept of infinite space contains within a fractal structure.
This in turns leads us to a new hypothesis for a universal theory of everything that examine the nature of reality from the micro to the macro as exhibiting the qualitative aspects of high dimensional solids. Object in 4th dimension or higher cannot be measured, and therefore are imperceptible to scientific investigation. However, a mathematics based on the laws of geometry (space), can explain many of the as of yet unanswered questions that confounds current investigation.
Aleph o.5
Russell Paradox
THE
Conclusion
So what does this tell us about infinity?
By placing our concept of number into a higher dimensional space, we find we can resolve the dilemmas present by infinity, that traditional mathematics, limited to the complex plane, cannot explain. Geometric Maths exposes an additional seven number space that have no definition under current axioms.
What are the consequences of Understanding Infiniy?
As the notion of the infinite is intrinsic to our experience of the universe, gaining a clearer understanding of its function allows us to develop an innovative new perspective about the nature of reality. This has led us to propose new explanations for many physical phenomena, that challenges the current human paradigm of how reality is constructed, and pushes the limitations about what is believed possible.
Carry On Learning
This article is part of our new theory, ‘Geometric Maths‘
Read the main article or browse more interesting post from the list below


Zero begins and ends all numbers
By examining the infinite nature in reciprocal numbers, we can ascertain that zero begins and also ends all numbers.
Solving the Russell Paradox: 2D geometric solution to the continuum hypothesis
The Russell Paradox arises from the fact that all numbers greater than 1 exhibit a reciprocal value. This is resolved by the folding of number space.

The Infinity of ONE
The Infinity of ONE is revealed by the nature of reiterated root calculations. This divides the number line into reciprocal and whole number space.
YOUR QUESTIONS ANSWERED
Got a Question? Then leave a comment below.

Question?
How can number exit in a higher number space?
ANSWER?
A line is a one dimensional structure. When the line is rotated, it creates the cross, see Zero². This transforms the line into a 2D plane. Similar processed turn the Zero³ plain into an X, Y and Z axis that is mapped on the hexagonal number plain.

Question?
How does folding or reflecting number space solve infinity?
ANSWER?
We propose that the infinite set of whole numbers is contained within a numerical space that is the same dimension as the reciprocals. This notion sees all real number above ONE reflected into the number space between ZERO and ONE. In this way, we have identified that these two number exhibit a unique relationship to square and root numbers. For more information, see our post on the Infinity of ONE and the ZERO boundary.