The Riemann Hypothesis is the number one mathematical challenge of today. We offer a geometric solution to the problem that is derived from 4th dimensional mathematics, which proves the conjecture to be true.
Overview
In this article, we present the geometric solution to the Reimann Hypothesi, which was calculated from the system of 4D Mathematic. By examining the nature of the complex number plane, through the lens of geometry, we can ascertain the process by which the number plane folds around the number one. Due to the correlation between the Silver and Golden Ratio, the plane can be bent and maintain its numerical integrity. However, this transformation causes the zero line to be translated to 0.5, forming the critical strip. This can be explained by the infinite density of reciprocal number space, which through our discovered of Aleph 0.5 exhibit exactly double the number of whole fractional parts compared to the whole number space.
The ‘compression of number space into a dot is accomplished by the diagonal of the square (√2) and the diagonal of a half square (√5), which allows for the hexagonal and square number planes to unify.
THE
Concept
The Geometric Solution
The concept of ∞+1 in 4th Dimensional mathematics causes the number line to rotate in numerical space, which is driven by the squaring of ZERO at the centre of the number line. (see rotational Squaring). As infinity can not exceed itself on the linear plane, it must move dimension in order to compensate for this extra number density.
Using this solution, we can enter the values for k into the 4D calculator, and examine the wave function. Where k=1 we enter the into the time function, as either -1, 0 or +1, we notice that only the values +1 and -1 produce a mathematically acceptable output, whereas the zero state produces the output x/0 = DIV0! This in normal mathematics has no solution, but in 4D maths produces the division of the number line into 2 infinite sets; positive, and negative. For this reason, the domain of the complex plane can only be extended into the negative by the bending of numerical space, through the process of analytic continuation.
In 4D maths we can use the secondary equation line in order to achieve the same result, which sets the critical strip from -1 – 0 – +1, instead of 0 – 0.5 – 1, as we do not need to bend number space which distorts the numerical results. In 4D mathematics, we can perform the equivalent of analytic continuation by folding number space over zero, which maintains the proportion of the infinite density’s aleph 0.5 for reciprocal space and Aleph 1 for whole number space.
Thus, we can explain the nature of the critical strip as the number ZERO is off-set by 0.5 through the bending of number space, which collapse of the infinite density of whole numbers, aleph 1, into reciprocal number space, aleph 0.5.


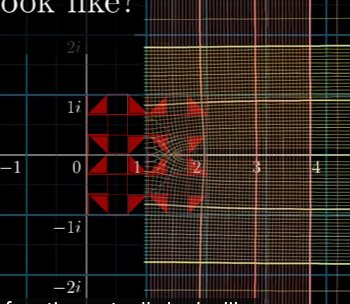
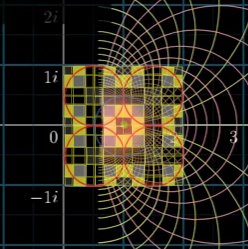
Stage 4 – The yellow square of whole number space is compressed into a dot where n=1 and the red numerical space now becomes fully wrapped around n=1 completing the critical strip.
Therefore, we find that the collapse of Aleph 1 (whole number space), through the bending of numerical space that creates the non-trivial zeros along the critical strip, instead of at the zero line. This is achieved by inverting the negative values of i into positive values, which is what the equation that produces the curvature is expressing. N= 1 to ∞, whereas the second side of the equation is the reciprocal of ns, which is an expression of reciprocal number law, n / n² = 1/n, on the complex plane.
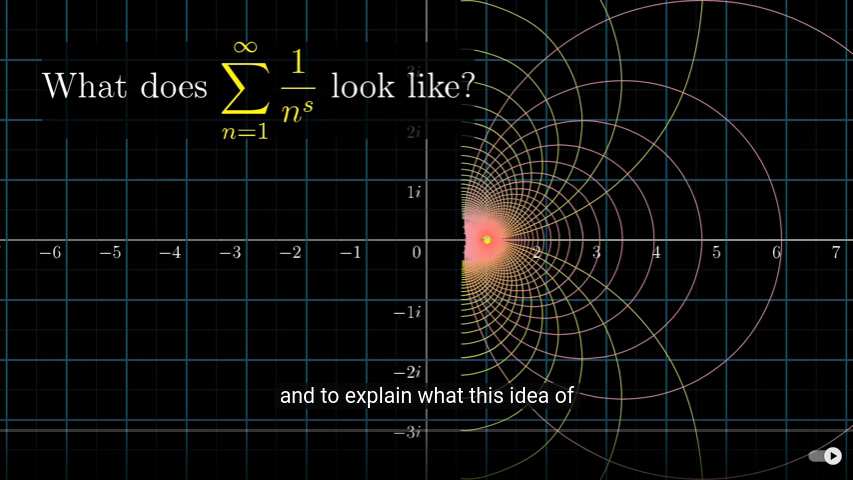
Bending the Square
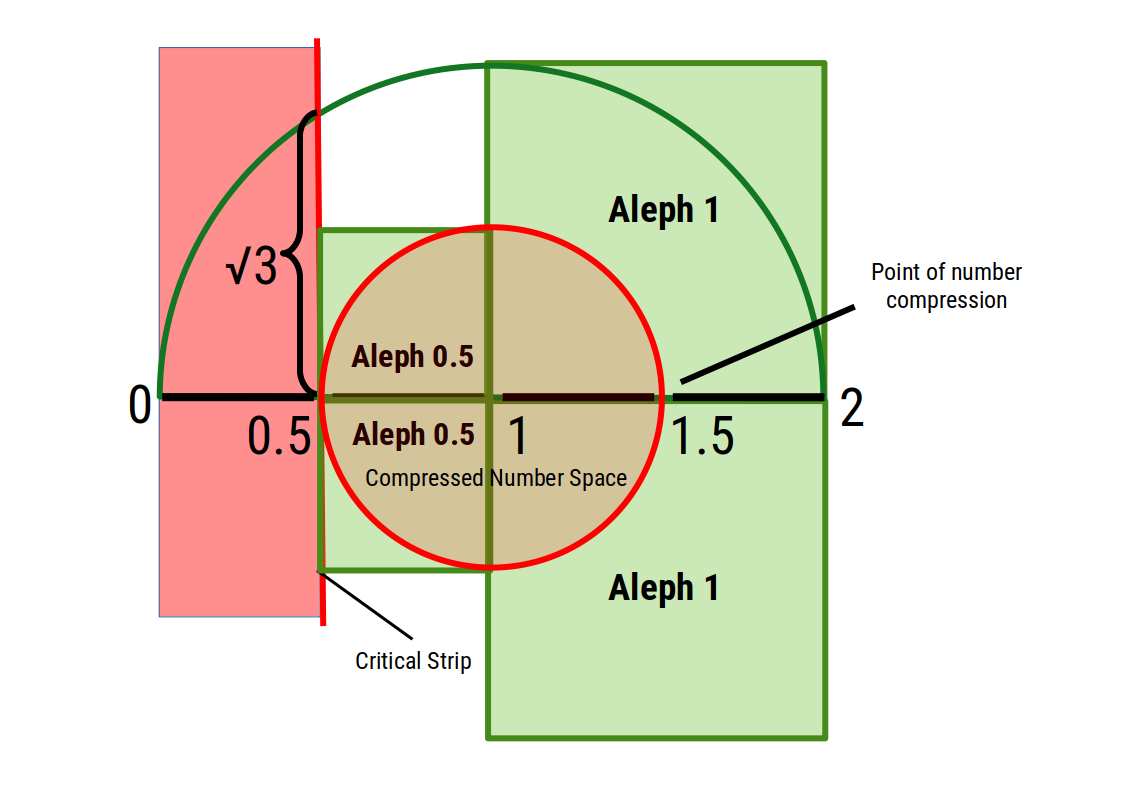
The number 2²= 4. We can see that in the 1st image above, the number 4 denotes the point where the red rectangle meets the yellow one. Yet on the complex plane, this numerical space is also represented as a square divided into 4 smaller squares. Half of the square lies in the whole number plane, whereas the other half in the reciprocal space between 0 and 1. As these spaces have an infinite density ratio of 0.5:1 (whole space is half as dense as reciprocal space), when the square is folded through the circle, the density of whole numbers is wrapped around the number 1, folding into reciprocal space. Therefore, instead of ending up at the number zero, it ends at the number 0.5, forming the critical strip.
In the image above, notice how the green circle shows how number 2 should fold to reflect onto the zero line. Instead, the arc collapses at the 0.5 mark, which is off by a distance of √3 in the vertical. As the number line is folds into reciprocal space, the infinite density increases to double, as denoted by Aleph 0.5.
Number compression of the Hexagonal plain
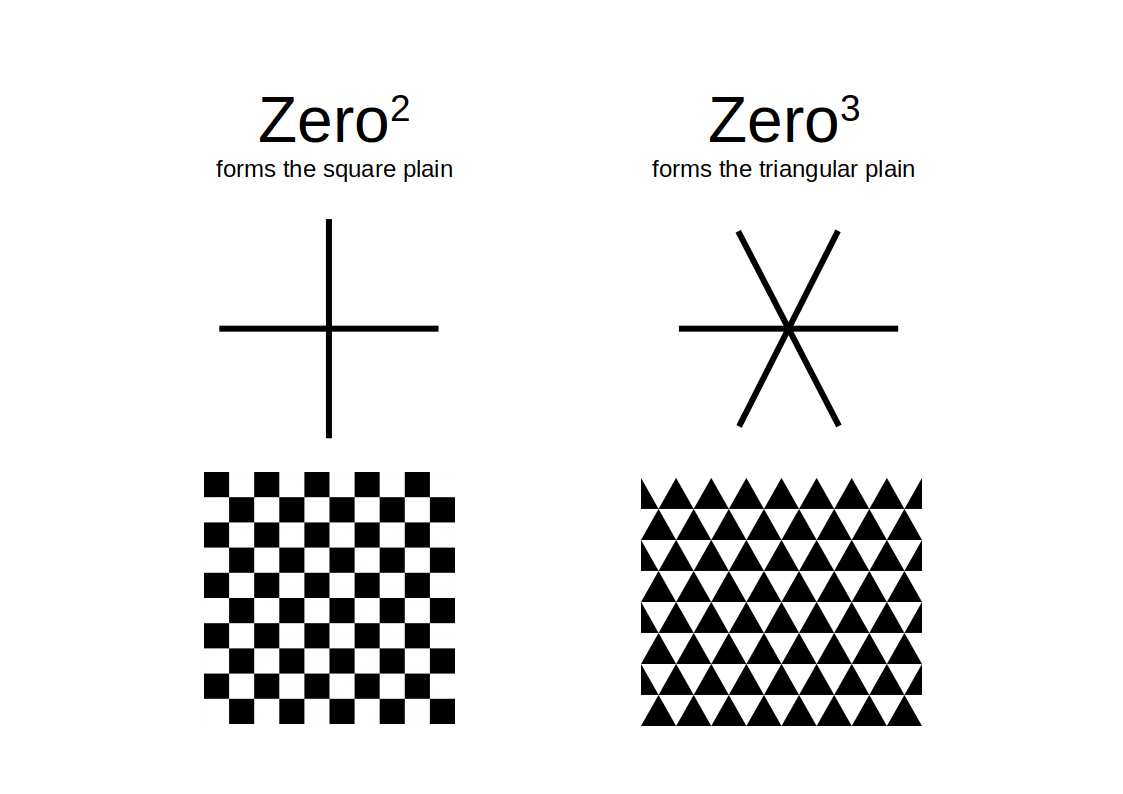
The complex plane is based on the square, which in Geometric Maths comes out of the notion of ZERO². The second number plain based is the triangle, which is not represented on the complex plane, but is represented in Geometric Maths derived from the notion of ZERO³. These produces the two types of regular 2D tapestries (formed only of 2 alternating colours), from the square and the triangle.
When we consider the nature of the hexagonal plane, we find that 6 triangles join to form a hexagon. This tapestry is created automatically from equal interlocking of two circles of the same dimension. This creates a geometric form called the Vesica Piscis. Once formed, more circles of the same dimension can be centred on the two nodes created to initiate the tapestry. The Vesica Piscis exhibits a ratio of 1:√3, which is reflected throughout the number plane.
The function f(s)=s² squares number space by rotating the x-axis through 180° and 90° rotation on the i plane. This alters the number density relationship of the whole numbers (Aleph 1) to the reciprocal space (aleph 0.5). However, instead of the points crossing at √3, (as per the triangular number plane) the number lines cross at the point of i2. This maintains a 90° angle at all intersecting points, instead of the 60° of the triangle, found on the zero³ plane.
We can examine this transformation from the perspective of the Silver and Golden ratio.
Notice how the i plane rotates 90° clockwise, whereas the real numbers rotate 180°
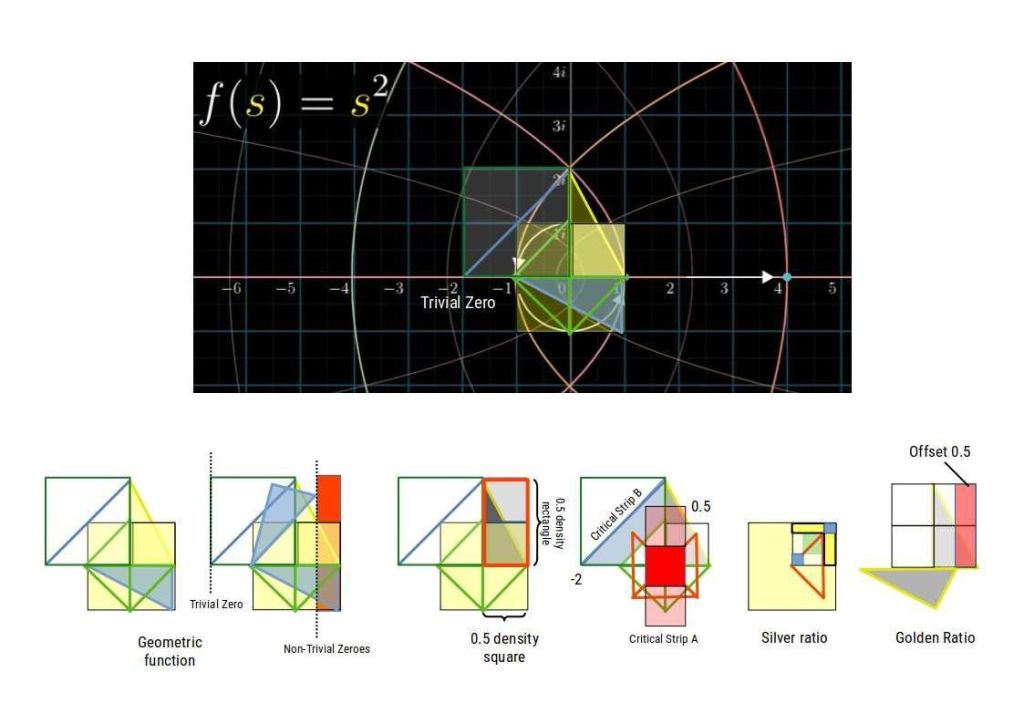
When we superimpose the silver mean and √2 fractal, the bending of the complex plain through analytic continuation matches the fractal pattern.
The Geometric Solution
Here we can see that the rotation of the plain move +2i to the number -2. Whereas, the value -1 is rotated double the distance, creating the offset in infinite density. The square (Diagonal √2) exactly half density of the rectangle (2 Squares, Diagonal √5). When the √5 triangle rotates, to lie along the same orientation as the √2 of the square, its corner point defines the halfway mark between 0 and +1, which creates the critical strip A. For this reason all non-trivial zeroes will fall on this line, just as any reciprocal square number series will devolve to zero.
On the negative side of the number plane, we notice a +2i arcs through number space to arrive at the -1 position on the number line. Normally, this rotation should find a position at n= -2. On the square plane, this offset forms a second critical strip (B) from the diagonal of the square in the negative plain, from a diagonal ratio of -√2:√8, which is a function of the silver ratio. However, on the positive plane the natural squaring function is not present, and √2:√8 is replaced with √5:2, which is a function of the golden ratio. Such as
When we examine the difference between the silver and golden ratio equations, both exhibit the function of ± 1. However, when the number √2 is replaced by √5, the whole equation must be halved to maintain this ± 1. From this, we can calculate the height triangle formed where √5 triangle touches the critical strip A as:
√((√5−√2)²−0.5²) = 0.652261205
To this value, we can add 1 to ascertain the distance from the zero point of the critical strip, and then multiply by √3 (the ratio of the triangular plain.)
1.652261205 × √3 = 2.861800354
The number is also very close to √8, producing a squared value of 8.189901266 (≈8.19), whereas multiplying the value by √3 results in a value just short of the number 5.
2.861800354×√3 = 4.956783614 ≈ 4.95678
We notice that 8.19 is a number formed of the digits 81 (9²) and 9, whereas the number sequence formed after this is 6180 which is the first 4 digits of the golden ratio. Whereas the number (28= 7×4) which is the number proceeding it multiplied by 10, (base 10, see subtraction of 7 below.)
When considered from the perspective of the Zero² (square) plain, a rectangle of sides 2:1 ratio produces a triangle with diagonal of √5, instead of √2 which is the full diagonal of the square of 1.
Next we can subtract √3+1 from 2.861800354 to find the difference = 0.129749546, which has a reciprocal value of 7.707156062. And then we find that √(7.707156062 – 7) = 0.500069696 = the critical strip. The number 7 is subtracted to de-π the value as 22/7 is close to π, and due to the nature of number e which demonstrates the difference in line length between the circle and hexagon in the triangular number plain.
See our SOLUTION FOR PI AND THE NUMBER E: ((2π−6)×(2.25×e) = 1.731999 ≈ √3)
Here, the value 2.25 is the relationship density x2 plus 0.5/2=0.25. This function is most easily expressed in geometric terms as:
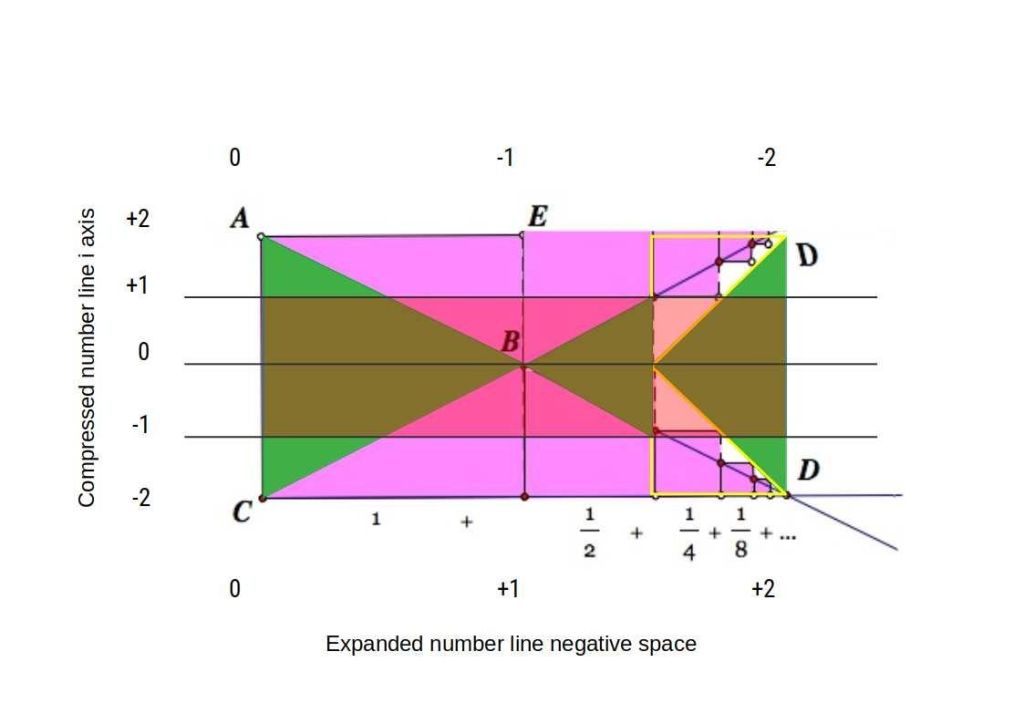
Here we see the reciprocal square number law has a limit of 1>∞ =2. The squares above 1² are reflected above and below, mirroring the density. The space left is formed of all reciprocal square numbers, from ¼ >∞ = 2, that have a diagonal of √0.5, which is also reflected on either side of the central line. As we compress the scale on the right to form the critical strip, so there is an expansion of number density along the x-axis, (negative plain of the zeta function).
If we make a final comparison of the rotation of the line on the triangular plane, we find that two unit rotations will produce a point on the critical strip that is at n=√3.
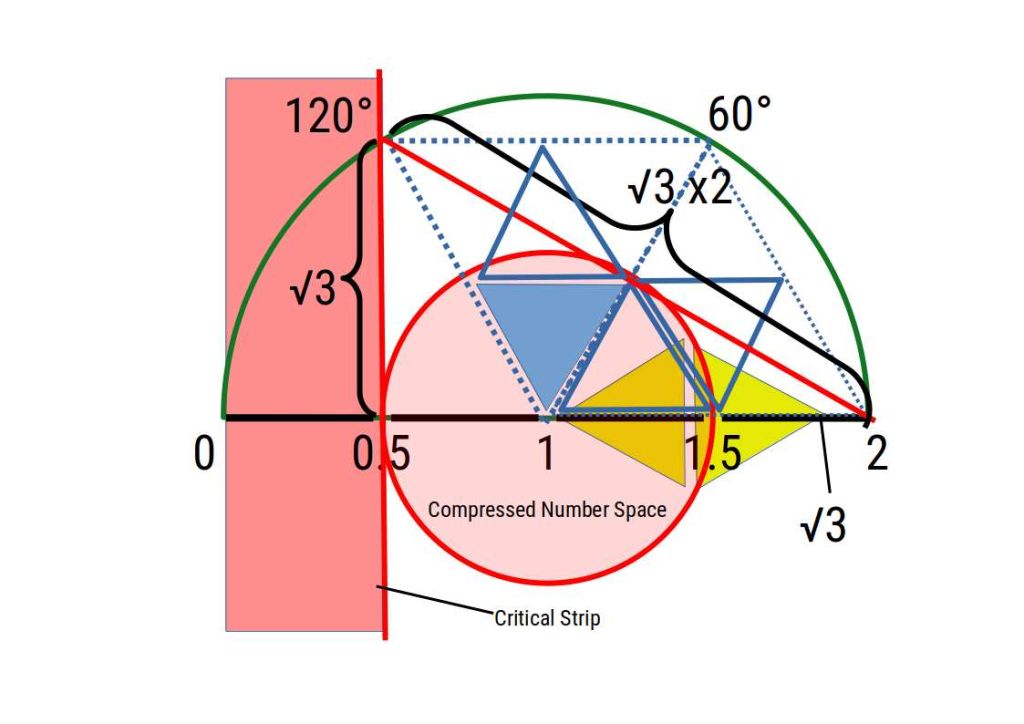
Therefore, when we multiply this by (√5-√2), we get a reciprocal value that is around √3+7. For those who are interested, we can square these numbers to get the ratio 3+49 = 52. As a function of π this becomes expressed as a ratio 3:49 in the following equation:
(( π /( 3 / 49 )) + 1 ) 2 ≈ √2
(( π /( 3 / 49 )) + 1 ) x 7 ≈ 10
√2:10 scaling function
As the Value for +2i rotates to position n=-1, however +i3 will rotate to the value of -1², simply because 3 x 4 = 12, which is produced from the squared values for √3 and 2. As the function f(s)=(s²) is a squaring function, this compression ratio √3² : 2² maintains the perfect 90° angle of the zeta function as it bends the number plane through the ratio π on the x plane to π/2 on the i plane.
π : π/2 = 2
( √3 / 2π )÷e ≈ 1
Where the result 1 in the second equation is equivalent to the +1 function in the √2:10 scaling equation. In Geometric Maths this relationship is defined by the simultaneous equation: Simultaneous equations for infinite density function of e
Function through 3
((2π÷√3)÷e)÷((π×√3)÷e) = 1 / 1.5
((π÷√3)÷e)÷((2π×√3)÷e) = 1 / 6
((2π÷√3)÷e)÷((2π×√3)÷e) = 1 / 3
((√3×π)÷e)÷((π×√3)÷e) = 1
((2π÷√3)÷e)÷((π÷√3)÷e) = 2
((π×√3)÷e)÷((π÷√3)÷e) = 3
Function through 2
((√3÷2π)÷e)÷((2π×√3)÷e) = ¼
((√3÷π)÷e)÷((2π×√3)÷e) = ½
((√3÷2π)÷e)÷((2π÷√3)÷e) = ¾
((√3×2π)÷e)÷((2π×√3)÷e) = 1
((π×√3)÷e)÷((2π÷√3)÷e) = 1.5
((2π ×√3)÷e)÷((π ×√3)÷e) = 2
((2π×√3)÷e)÷((2π÷√3)÷e) = 3
√12π ÷e ≈ 4
Notice that the zero point of the critical strip (n=0.5) is formed by an equation with a ratio of π : 2π. For more information on the function of e can be demonstrated by the e-ratio calculator.
This function is more easily demonstrated by the following geometric presentation that shows how the density of two squares with a surface of area of 1.5 are compressed into the triangular plane through the number e.
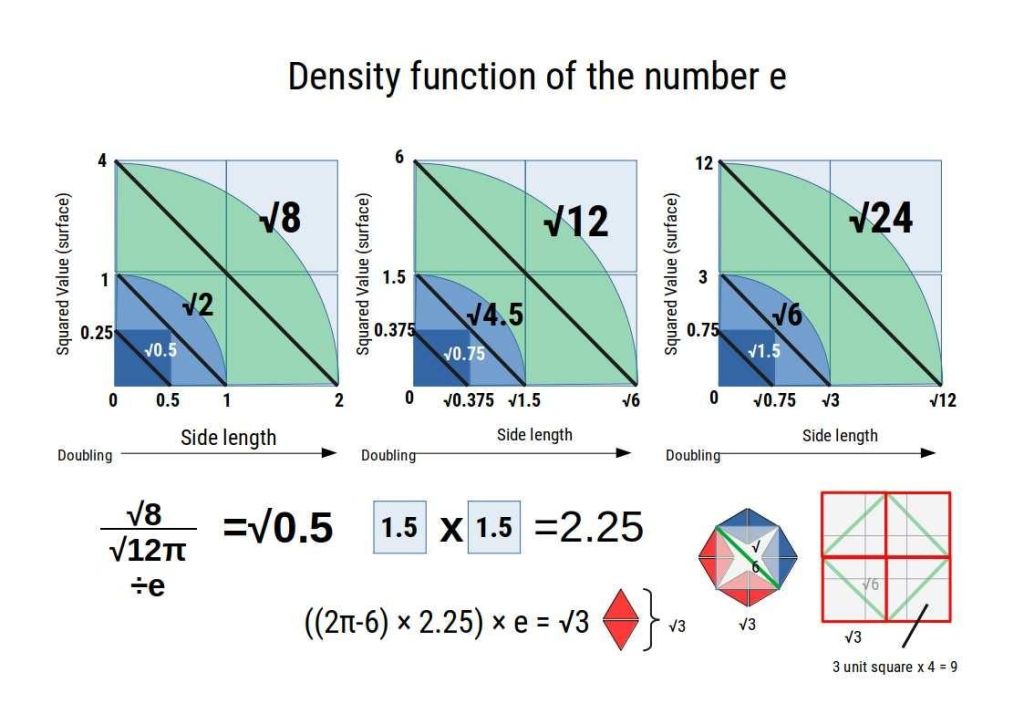
Therefore, 2.25 / √3 = 1.299038106 = √1.6875 ≈ 1.3
Notice that the square of 4 overlays the square of nine (bottom left), with equal density.
Number unit compression
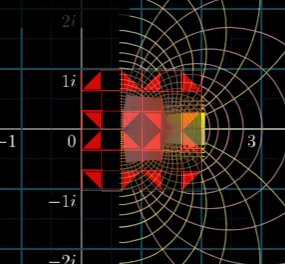
If we examine the analytic transformation of the zeta plane, we see the ‘red’ dot accumulates first at point n=1.5, which moves towards the √3 before collapsing into the number one. This is due to the infinite density of numbers on the hexagonal plane. The number e is the accumulation of all reciprocal factorials, which are a series of triangular numbers added together in time. I.e. the collapsing of number space into a dot. This is what is happening when the complex plane is transformed. However, as the plane is bent instead of being folded, the numbers are compressed into the triangular plane, which is the genesis of the hexagon in a circle.
This is expressed in Geometric Maths by the equation:
((2π-6) × 2.25) × e = √3
Here, a circle with the radius of 1 has the 6 sides of the hexagon removed from its value. The remainder is the difference between the circumference and parameter of the hexagon. This is multiplied by 2.25 to form the ‘infinite density constant’ (unique to Geometric Maths). As the number e represents the infinite density of all numbers in reciprocal space compressed into a dot, the √3 represents the unit distance between the 2 tips of opposing triangles.
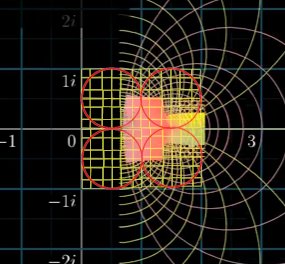
We can see from the image above that when rotated 180°, the unit measure between the start and end point is double √3. Therefore, the equation becomes:
((2π-6) × 4.5) × e = √12
((2π-6) × 3) × (e ÷2) = √3 / 2
However, in 4D mathematics whose axioms accept the concept of negative squaring, due to the fact of the law of order (e.g: 2 x 3 is NOT 3 x 2 in 4D Maths), the 4 functions of squaring (++, – -, + -, and – +), means that the above equation becomes expressed in terms of the number 9.
((2π-6) × 9) × e = √24
This is the ‘real’ equation in 4D mathematical space, that will never be expressed on a complex number plane that is missing ¾ of all numbers.

The hexagon divides 2π into 6 parts. When multiplied by 9 we get 1.5 hexagons, which will rotate around the circle 1.5 times to end at the negative side of the number line. The square, on the other hand, will perform the same rotation (1.5) in six steps. Therefore, 6 squares x 1.5 = 9, where the two types of plane unify. However, as the zeta function bends the square number plane (complex plane) in both, the up and down direction from the real number line, the number e is produced at half density.
((2π-6) × 9) × (e ÷2) = √12
Furthermore, the rotation of number compression is accomplished through a single rotation of 180°, which is 2 steps on the square plane and 3 steps on the triangular plane. Therefore, we get:
((2π-6) × 3) × (e ÷2) = √3 / 2
In Geometric Maths, the number √3 /2 is found as the diagonal of a cube side length 0.5. Normally, this describes a hyper-cubic number space, a concept that is beyond the capabilities of the complex plane to express, as it excludes the function of negative squaring. The result is that the bending of number space of the zeta function can only accommodate numbers >+1, and no negative numbers.
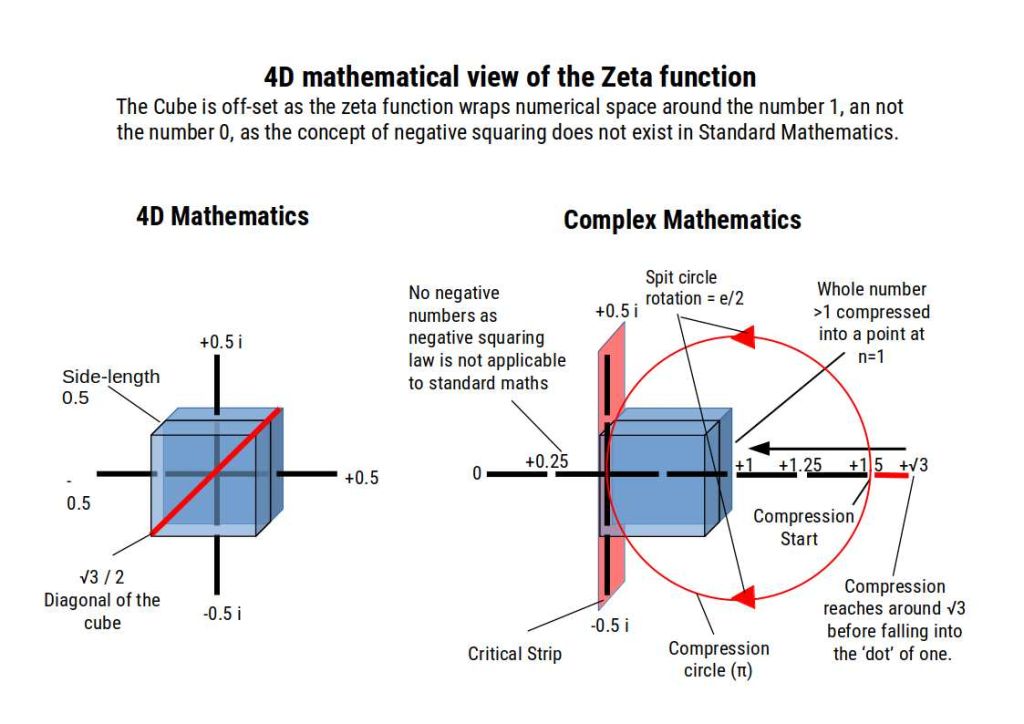
In Geometric Maths, the zeta function is depicted as a cube of number space that becomes flattened into a square and off-set when expressed on the complex plane. In the next section, we explain how 4D space exposes the correct views of number space beyond the number line, and the methods employed to calculate the infinite densities of all real numbers greater than 1.
THE
Conclusion
How Does this Solve the Riemann Hypothesis?
We can solve the problem through simple geometry, whereby the Golden and Silver Ratio are employed to demonstrate how the complex number plane can be folded, and yet still offer an analytic continuation that is geometrically coherent. The geometric solution is explained in more detail in terms of infinite density function and Geometric Maths, which offers a novel new kind of numerical space that does not express √-1 in the traditional sense.
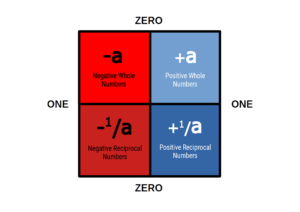
The complex plain VS infinite density function
In Geometric maths we employ the conept of infinite dencity function, which explores the nature of infinity from the perspective of a unit length. When a line is increase in length, so its infinite density decreases relative to the numerical space between zero and one. Root number are geometrically positioned at a 45° angle to a square, defining the density function between two number lines placed at 90° to each other. The complex plain places the root value of -1 at a 90° angle, which in turn leads to the ‘unit circle, which is unable to represent reciprocal numbers in the correct infinite density (Aleph 0.5). Therefore the critical strip will always act as a zero point instead of the zero line.
Carry On Learning
This article is part of our new theory, ‘Maths of Infinity‘
Read the main article or browse more interesting post from the list below

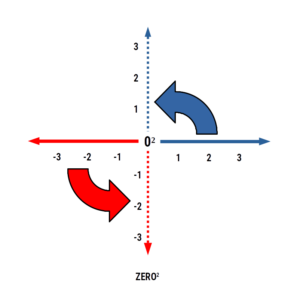
Zero²
ZERO² is a geometric function that rotates the entire number line at 90° to the original, to produce an X,Y co-ordinate system. Overview When we perform any kind of mathematical calculation involving zero, the result always appears to be zero. Yet zero calculations can be performed. For example, the number

Zero begins and ends all numbers
By examining the infinite nature in reciprocal numbers, we can ascertain that zero begins and also ends all numbers.
8 Infinities on the Number Line
There are 8 distinct infinite boundaries that appear on the number line. Two either side of Zero, four that are found either side of the number +ONE and -ONE, and the final pair that is the infinite series of whole numbers, which increase towards infinity. Overview It is a mathematical
YOUR QUESTIONS ANSWERED
Got a Question? Then leave a comment below.

Question?
Some of the mathematics seems quite unusual in your proposed solution. how can you express infinity as a number?
ANSWER?
When wxamining infinity, we tend to subtract infinite sets rather than add numbers as is traditional in mathematics. Before reading this post we recomend familuarising yourself with the notions proposed by Geometric Maths.

Question?
This idea seems to be that the number plane is folded through a specific geometry, but what about this 4D mathematical solution?
ANSWER?
This solution was devolved from our investigation into 4D mathematics, which is a different system of number. This makes it hard for tradintional mathematicians to work with. Instead concepts such as phi and the silver ratio are well documented. Therfore this geometric solution provides acleaner explaination. You can also explore the nature of 4D math on this site.
STILL Looking for Answers?
Ask a question…