The numbers π and the number ℮ are considered to be transcendental in nature, as there is no algebraic root that can define these constants. For this reason, these numbers have held particular interest for mathematicians, as a kind of numerical enigma. In this article, we begin to decode this mystery, through a set of simple algebraic equations that sheds new light on the elusive numbers.
Overview
The transcendent nature of π and the number ℮ is resolved through the understanding that numbers in base 10 create distorted values when expressed as a decimal value. Through the examination of the nature of geometry, we can decode the nature of these two numbers, and realise that the reason they are considered transcendental is because they are found to divide the number line so that it appears irrational. By employing our new mathematical technique of simultaneous equation, we can produce whole number results from a combination of π, ℮, and √3. This can be express on a simple excel spreadsheet, which explores these geometric constants.
π and the number ℮ Calculator
Experiment online
KEy Points
-
π, the number ℮ and √3 can be unified into a whole number
-
The equation that demonstrates this is ((2π - 6) * e) / √3.
-
This established the non-transendant nature of π and the number ℮
THE
Concept
π equations
The non-transcendent nature of π and ℮ is resolved through various equations that use a ‘reduced’ value for √3. This is because the infinite fractional values of both π and ℮ express a distortion in base 10. However, by examining a few different equations simultaneously, we can begin to understand the deeper relationship between these irrational and transcendental numbers.
The first equation to consider is:
This produces a result very close to one, however, as we will see, we can account for this discrepancy by the nature of base 10 distortion of the number π and ℮. First, we should make sense of this equation, in order to recognise this fact more clearly.
Number e and √3
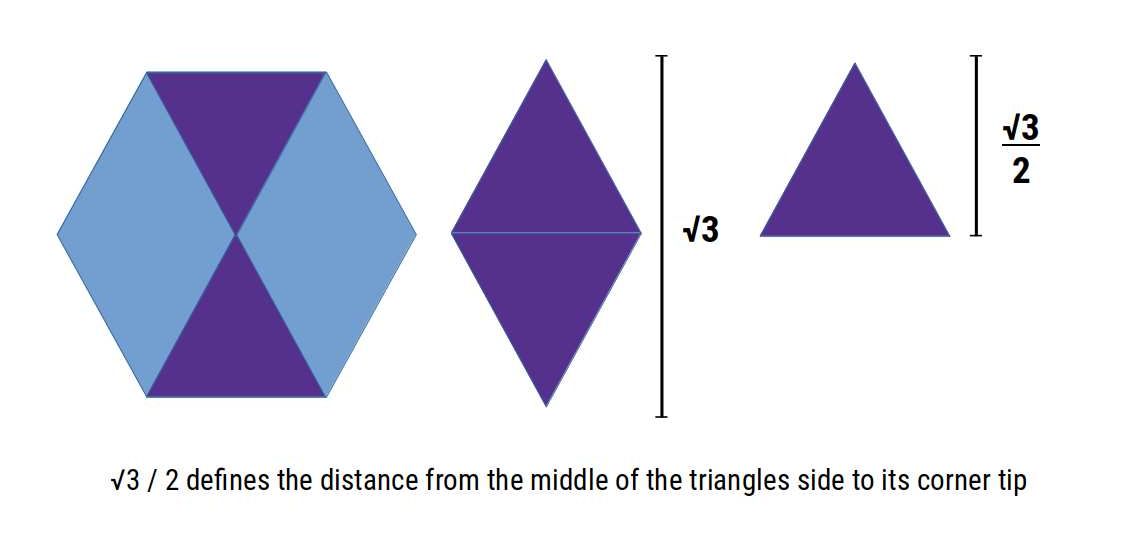
The √3 is a geometric ratio found in both a hexagon or more appropriately two equilateral triangles placed on top of each other. When we divide √3 by 2, we half its length, which defines the distance between the midpoint of one of the triangles sides to its corner tip.
Next we can consider the nature of the number ℮. The formula that generates ℮ is found to be constructed from the addition of the infinite series of reciprocal factorials.
In this equation, k= the infinite set of whole numbers from zero to infinity. A factorial is denoted as x!. A factorial is a series of sequential numbers multiplied together.
The number ℮ is found by adding the reciprocal value for each factorial for the entire infinite set. But what does this have to do with a triangle? As we progress through the factorials, each number series grows by an extra unit number. We can represent this in a triangular formation.
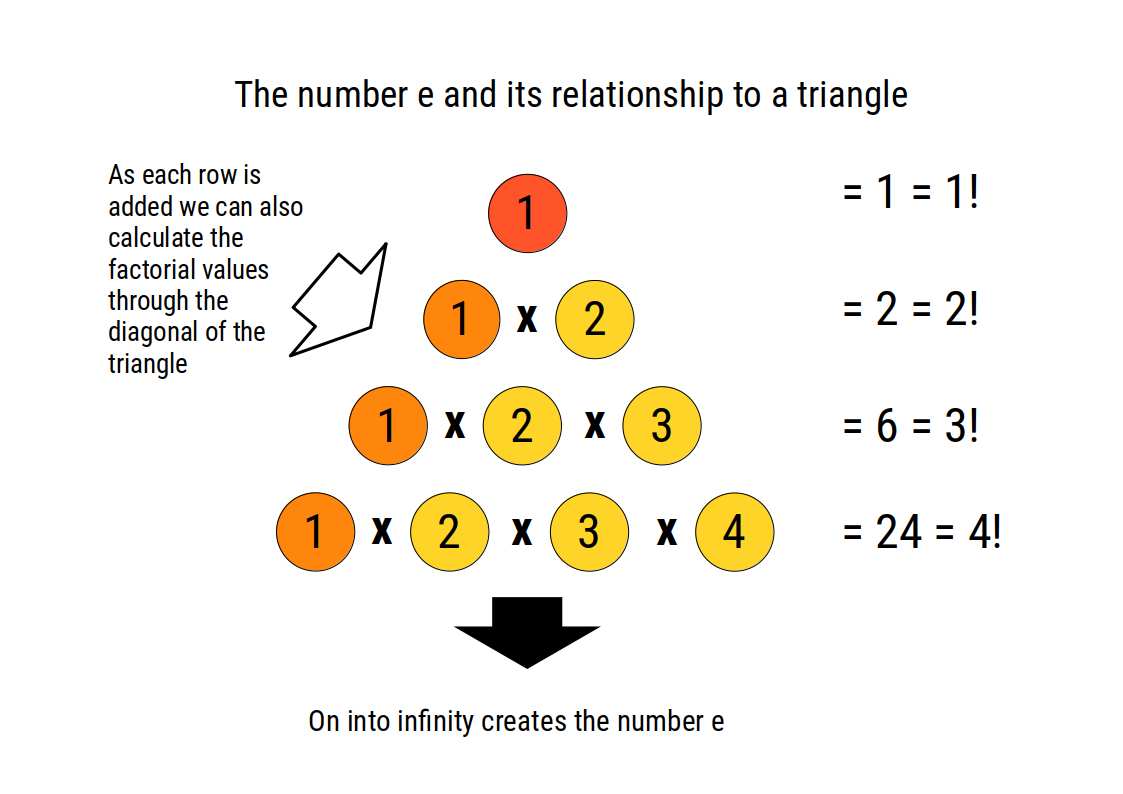
In the case of the number ℮, the units of each new row are multiplied together to create the next factorial, and then each row is added together.In the above image we can see that the factorials in a triangle can be calculated in two directions. As the numbers expand downwards (black arrow) so the line expands in length. Yet in the diagonal direction (white arrow) a new number is added to the bottom right of the triangle. two sides of the triangle are therefore constructed from an infinitely increasing set of numbers, whereas the third side is made of in infinite set of ones.
In the image above each number unit is shown as a whole number for simplicity. However the number ℮ is constructed from the reciprocal values of each number. This means that each result is expressed as a fraction between zero and one. This is best express as a unit line length rather than unit counters.
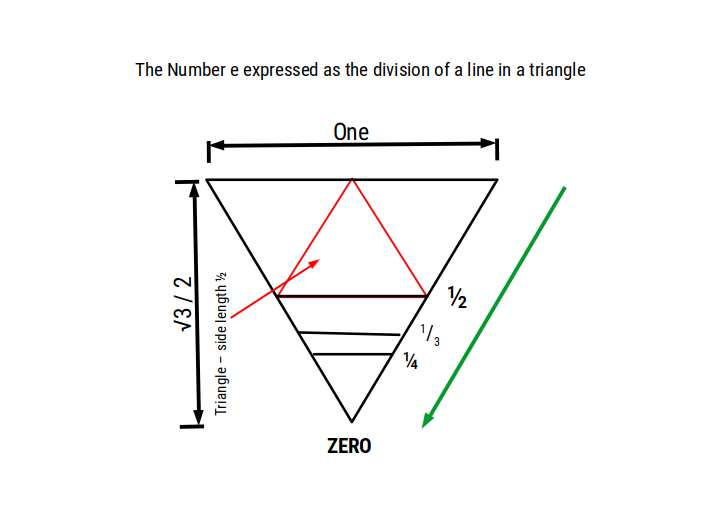
The reciprocal line lengths that form the number e are found within a triangle side length 1. The point of the triangle represents zero, which is the infinite boundary for the successive reciprocals. Each new line is multiplied by the existing set, to form the factorial for that particular number. As the line diminishes into infinity, it will traverse the distance of √3÷2.
This explains the equation in terms of geometry. The distance between the starting line and its opposite zero point is (√3÷2), which contains the infinite set reciprocal numbers. When divided by the number e, the result is about 1÷π. Therefore, when we multiply the answer by π we get 1.000998, roughly one.
π equation 2
In this next section, we will begin to identify why the division of √3÷2 by the number e should produce the reciprocal value of π. This can be explored by the following equation, where we multiply the number e by √3÷2.
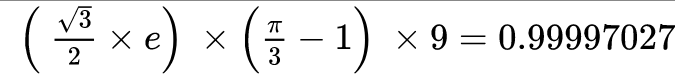
In the second half of the equation, we have the value (π÷3) – 1. Mathematical π is defined as the relationship of a circle’s diameter to its circumference. So if we take a circle with a radius of 1, then the circumference will be 2π. A hexagon with a side length of 1 can be placed inside such a circle. This in turn is formed of 6 triangles. One of the outer edges of the triangle (length one) has a curvature with an arc distance of π÷3.
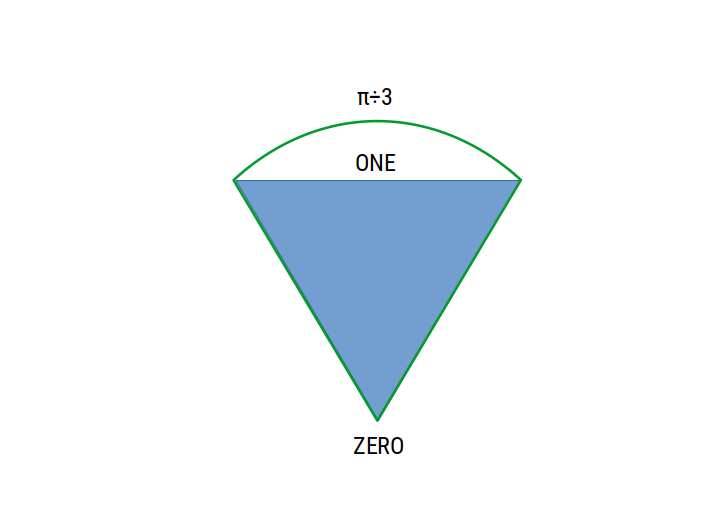
The value of (π÷3) – 1 is therefore the difference between the arc and the straight line. Returning to our equation, we can see that the first part of the equation is found to calculate the number e in terms of the surface area of the triangle. When this is multiplied by the difference between the line of one and the arc, the result is roughly one ninth.
As the line diminishes towards zero, so its difference to the arc will also get smaller. At the level of the infinite, this difference will still remain, causing a discrepancy in the numerical result. In the above equation, the value of 0.999999… is the infinite boundary that approaches ONE. The exact value drops two places to 7 in the fifth position. When we examine this remainder without multiplying the result by 9 we find it is very close to √0.5.
Geometrically this is found as a line that stems from the centre of a square, side length 1, to its corner. However, it is also the reciprocal value of √2. (1/√2 = √0.5). These ratios are indicative of a square. We can compare the half square and half triangle, and find that both √3 and √2 define the distance from the centre of a side to the tip, representing zero.
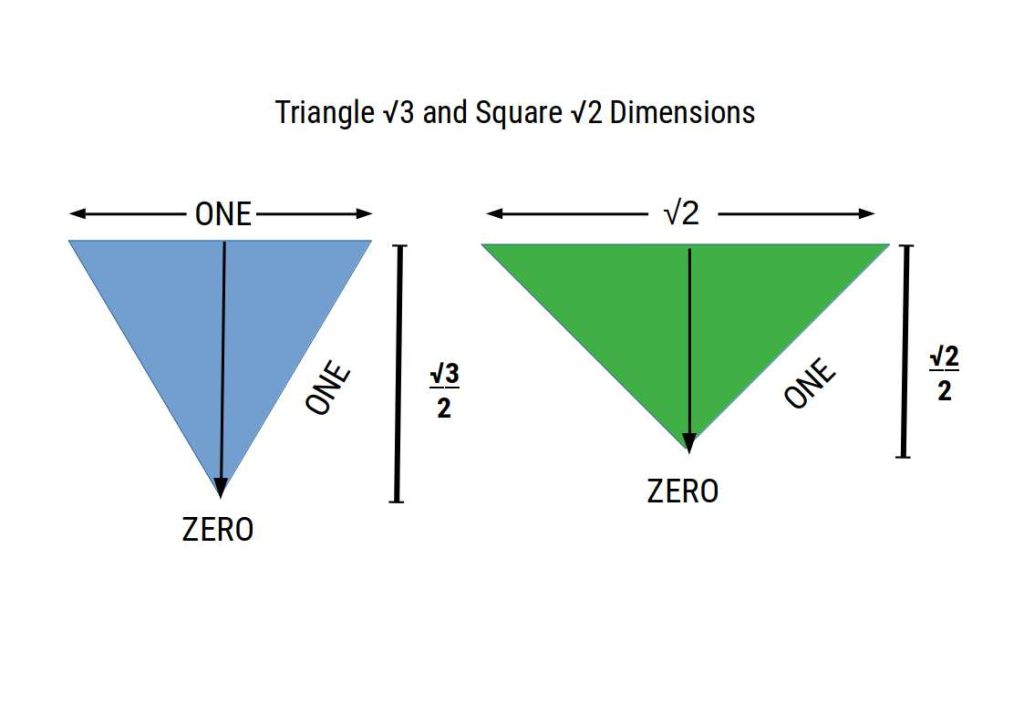
The fact that a value close to √0.5 is found in the remainder is explained in more detail in our theory of Geometric Maths, and our solution to the Riemann Hypothesis.
If we subtract √0.5 from the number ℮, we find the result is just over the number 2. It is a curious fact that the traditional value for the number e is formed including 0!=1*, followed by 1!=1. If we remove these values from the equation, then we find that the remainder is extremely close to √0.5 + 1/90.
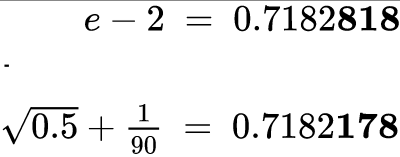
NOTE: 818 – 178 = 640. 64 is 8²
This simple relationship of the number e and √0.5 is curious, as 2!=0.5. This means that by excluding 0! and 1! from the formation of the number e, the collective infinite set of reciprocal factorials above 2 will roughly equal √0.5 – 0.5, which can also be expressed as (-1+√2)/2.
The reciprocal value of √0.5-0.5 is equal to √8+2. In our geometric solution to π and the Riemann Hypothesis we utilise the ‘silver ratio’ which is defined by √2±1, which is half the value of √8+2. Therefore, we find that (√0.5-0.5) x 2 = √2-1, which is one of the expression of the silver ratio.
1/9 and the geometry of infinite reciprocals.
The qualities of 1/9 can be explored through the nature of fractal geometry. When the side length of a triangle is divided in half, it can be divided into four smaller triangles. When the line is divided into 3, so nine triangles can be placed inside, However, a line divided into 4 produces a fractal pattern that superimposes itself perfectly over the triangles created by the division of the side in half. This is because the number 4 is the first in the series of number not to be a prime. Note that the number one is not considered to be a prime number, yet it still exhibits the quality of a prime, acting as a numerical ‘container’ of the infinite set of reciprocal values.
In the image above, we can see that after the third step, the geometric pattern changes. At this point, the midsection can form ‘outward facing’ triangles. The main body of the triangle is divided into 9 smaller parts (1/9). In the fourth step, the triangle is divided into 16 parts. Here there is an overlap with the triangle that has sides divided into 2 in the second step. This is because the number 4 is not a prime number. This will begin to make a distortion in our result, as we are using a base 10 system. In the fifth step, the triangle is divided into 25 parts, which is 1/4 of 100. Yet is also 5².
Returning to our second equation, we can see that the first 4 digits of the reciprocal are 0.1111. After which the next 2 numbers are 07. Here we find that the discrepancy is 1/250000, which when multiplied by 1,000,000 equals 4.
The value 1/9 is equal to 0.111111… recurring, and it is this nature that creates a distortion in our results, leading us to believe that π and ℮ are transcendent in nature. Next, we can examine the nature of these simple reoccurring number fractions.
1/9 and the boundary of infinity
As we operate in base 10, the number nine is the last ‘number’ before we begin to add additional digits to form higher numbers. When a number is expressed as a double digit, it will create a distortion in certain calculations, especially when performing infinite iterations. This table shows the reciprocal nature of the reciprocal values of 9.
And so on.
Here we can see the simple pattern of infinite number series. Whatever number appears at the top of the fraction, is reflected as in infinite series of the same number in its reciprocal fraction. This is valid until we reach the final step where 9/9=1 not 0.999999… but is that really the case? If we shorten the values of the reciprocal to a specific length, we find that we get a different result
What we see here is that the infinite fraction of 1/9 actually ends with the number 1. As more nines are added to the decimal fraction, the number one does not disappear. It remains at the end of the infinite set. Yet, as the fraction grows in size, we will round up the value to equal 9. This is perfectly fine if we are focused on traditional mathematics, however, when working with the infinite, these result cannot be discarded. Instead, we need to recognise that there are certain numbers that will exist at the end of an infinite set. We introduce the notion of 1.000→∞-1 to express this concept mathematically. Here, the number one is accompanied by an infinite set of zeroes. At the end of the infinite set we subtract 1 to represent the maximum value before a number becomes whole, in this case 1. In consideration of the nature of the number nine, we find that the value expressed in these terms is 9.000→∞-9.
It is through examining the nature of numbers at the end of the infinite that we can decode the base 10 distortion, a subject cover in more detail in our maths of infinity.
Solving π and the number ℮ with simultaneous calculation
In order for us to resolve these inconstancies created by the nature of base 10, and infinite reciprocal values, we have created a mathematical process we call ‘simultaneous calculation’. By performing two mathematical calculations, we can add the result together and see if the ‘pieces’ form a whole number. Similar to two pieces in a jigsaw, that when match will produce the whole picture.
To achieve this, we will use a reduced version of our π equation, that should produce a result of 0.5. Then we can marry it with a ‘reciprocal’ calculation, and add the results together.
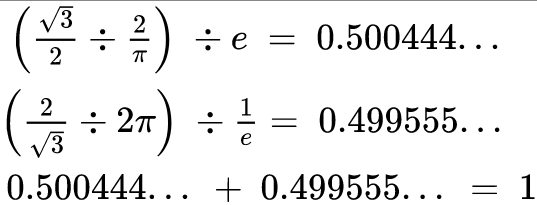
Here we find that when the result of the π equations, whole and reciprocal, are added together, the result is equal to 1.
What this shows is that the transcendent nature of π and the number e is to do with the nature of our base 10 system of counting, which produces infinite fractions that do not resolve. Not that the numbers are transcendent. For example, the same can be said of many other mathematically accepted solutions for convergent series.
The reciprocals of all square numbers converge at 2
The reciprocals of all trinalge numbers converge at 2
In current mathematical understanding, the above calculations for square and triangle reciprocals both seem to converge at the same number. Yet the actual result is not the same. This is because the number series is clearly different, and so the results of each will resolve in a completely different way. The calculation will never actually equal the number 2. The final boundary is at maximum 1.9999… but even that is not the case. Each of these two series converge at different rates. In 4th dimensional mathematics, we qualify the rate of convergence for each infinite series. What we find is that all numbers produce unique ‘dissolution’ waves. Within this novel numerical space, we find that all numbers are non-transcendent.
THE
Conclusion
What does this tell us about π and ℮ ?
The belief of the transcendent nature of π and the number ℮ is derived from the nature of reciprocal and decimal values that are expressed in base 10. From this view, π and the number ℮ are non-transcendent, just as all other infinite convergent series. The equation ((√3/2)/e) x π = 1 can be expressed in geometry, by which the numerical nature of these constants is revealed.
What is the significance of π and the number ℮ being non transcendental.
Modern mathematics has built is axiomatic foundations by categorising numbers in a particular way. This categorisation has led mathematicians to perceive numbers through a particular perspective that is not particularly effective at dealing with the infinite nature of numbers. Our algebraic solution, present here, suggest a re-categorisation of number, which in turn radically alters modern mathematics. This solution is presented, translated in 4th dimensional mathematics, into a form more acceptable to the current system of numbers. More exact solutions to π and the number ℮ are presented in the context of 4th dimensional maths, where we are able to penetrate the infinite nature of numbers far more effectively. This is in turn solves many of the paradoxes presented by conjectures such as the Continuum Hypothesis.
Carry On Learning
This article is part of our new theory, ‘Maths of Infinity‘
Read the main article or browse more interesting post from the list below
What is the continuum hypothesis?
The Continuum Hypothesis was the #1 mathematical challenge set by Hilbert at the start of the 1900’s. It was only ever solved in the negative.
Zero²
ZERO² is a geometric function that rotates the entire number line at 90° to the original, to produce an X,Y co-ordinate system. Overview When we perform any kind of mathematical calculation involving zero, the result always appears to be zero. Yet zero calculations can be performed. For example, the number
Reciprocal number space
All numbers beyond ONE have a reciprocal representation between the numbers ZERO and ONE. It is this mirror-like nature of reciprocal space that allows us to conclude that the number ZERO terminates the series of infinite whole numbers. Overview Within the ‘Reciprocal Space’ between Zero and One, find all numbers
YOUR QUESTIONS ANSWERED
Got a Question? Then leave a comment below.
Question?
I followed your calculations but, we find that the results are never exactly a whole number, even in the ‘simultaneous’ calculation. The result is not exactly 1.
ANSWER?
To understand the exact nature of base 10 distortion, we have included geometric examples that express the nature of π and the number ℮. More accurate solutions are produced in our 4th dimensional mathematics. However, as we have found that for some mathematicians, this new mathematical space upsets many of the assumption that form the axiomatic background of modern maths. For this reason, we have produced an algebraic solution more in alignment with current mathematical thinking.
Question?
I understand what you are explaining intuitively, but what do the dimensions of a triangle and square have to do with the number π and ℮?
ANSWER?
In the maths of infinity, the surface area of a triangle comprises an infinite set of numbers diminishing towards zero. A surface of a square represent a different type of infinite set, formed by number lines that are exactly the same length. Therefore, a square side length one has a surface formed of an infinite set of lines, with a uniform length of one, and the triangle an infinite set of lines reducing from one to a zero point. These are the only regular shapes to fill a 2D plane uniformly using just two colours. In geometric maths, these are the two kinds of 2D number plane.
STILL Looking for Answers?
Ask a question…
