By examining scientific constants in terms of ratio and geometry, Dimensionless Science offers a system that is simple to understand and accurate enough to be compatible with conventional scientific notation.
Overview
If you thought science was all about measuring, then our new system of Dimensionless Science may come as quite a surprise. Based on the simple idea that the universe can be explained through simple ratio, we have found that complex formula can be collapsed into simple geometric images. The validity of this system of ratio is supported by the fact that it remains consistent for scientific calculations at both the macro and microscales of reality. Thus far, our system of Dimensionless Science has defined the exact values for over 40 constants and pieces them together in a simple way.
This includes fundamental constants such as the Speed of light (c), the Electromagnetic constants (ε0, υ0, and Z0), the elementary charge (e), the Fine structure constant (α), and the Planck constant (h). Under the presently adopted SI system, used by the standard model of science, these constants do not have exact values defined.
However, once expressed as a ratio, we can find exact values to any arbitrary number of decimal places. The apparent complexity of defined values of the SI system is explained as the combination of irrational numbers such as π and various other root numbers. Whilst no one knows the exact number of these ratios, we can calculate them to a much higher degree of accuracy.
However, the real revolution for this kind of geometric metamathematics, is that it can be precisely expressed in terms of simple geometry. This opens the door for a new way for people to comprehend science that is much simpler and more intuitive.
THE
Concept
What is Dimensionless Science?
Dimensionless Science is the examination of mathematical formulas and scientific constants as ratio that is expressed through the lens of geometry. From the perspective of quantised reality, it assumes that this arises out of the geometric nature of space itself. Energy that fills this space does so in conformity to this structure. However, as we are embedded in space, we cannot directly measure this nature. 4D space needs to be conceptualised, as it is beyond our realm of experience.
Simple Ratio
For many, the complexity of scientific equations reads like a foreign language. Specially designed mathematical symbols can convey complex ideas quickly to the trained eye, but this requires dedication and years of training. But what if there was a way to decode the complexity, in simple enough terms for anyone with an eye for art and knowledge of geometry to understand.
Dimensionless Science aims to do just that. At its foundation is the idea that all scientific constants and formula can be perfectly described using simple ratios, and geometric constants. Through a process of dimensional analysis, we can examine the nature of scientific constants and their relationship to each other. Through this we are able to establish exact values for important constants such as:
3
The electromagnetic constant (e0)
The magnetic constant (U0)
π/2
Elementary Charge (e)
Fine Structure Constant (α)
√(3³/4³) × π²
Planck Constant (h)
Everything is Relative
Dimensionless Science provides a framework that does not require any direct measurement. Rather, it extrapolates the ratios found in existing scientific formulas, that can then be ascribed to certain geometric functions. Dimensionless Science reconciles the relativistic nature of time and space, which exhibit time dilation and length contraction when travelling at high velocity.
Therefore, rather than using units of space and time as its foundation, Dimensionless Science drives its base units from the energy in the vacuum, whereby the speed of light is set to 3 and the constant u0 to 4π. From this basis, exact values for Z0 and e0 are ascertained, which provides the foundation for the exact values for a vast number of Scientific Constants to be ascertained.
Dimensional Analysis
When we think about measuring a quantity of something in reality, we generally choose the correct kind of units to represent the phenomena we are examining. Water is a fluid and is defined in terms of litres, or pints. Solids we weigh in KG, or ounces. Time we measure in seconds and minutes and space unit of length, such as the meter or centimetre. It does not make any sense to ask how fast is a loaf of bread. These different types of measurement are called dimensions. Dimensional analysis asserts that only quantities that exhibit the same dimension may be compared, add, or subtracted. This is called dimensional homogeneity.
However, phenomena that hold different qualities may be multiplied or divided.
To be clear, we can take the weight of 2 people and add or subtract them as the quantities exhibit the same dimension, and so the result is meaningful. However, the same cannot be said if we take the weight of one person and the height of another. In this case, addition and subtraction of the quantities holds no meaning.
However, we can take height and weight and divide or multiply them to produce a relationship between the two. This implies that mathematical functions that use multiplication and division are in fact dimensionless operations, that can accept units of different qualities. This is interesting as most scientific equations are also predicated on ratio, the relationships of quantities found through division or multiplication of various values.
For example, the equations for Newton’s Laws of motion have values for mass and distance, that make sense in regard to which units are chosen to define weight and distance. When changing between different systems of measurement we simply employ a conversion factor, which is also a dimensionless quantity, as it mealy express one unit of measure in units of another. Reality is not affected by our choice of measurement unit and so units are arbitrary.
Scientific Constants are all ratio
Quantity A x quantity B = quantity C quantity C / quantity A = quantity B quantity C / quantity B = quantity A
The concepts of dimensional analysis are actually already found strewn throughout science, which has adopted a variety of different measurement systems adapted for examining different types of phenomena. Such systems adjust the scale of measurement so that key values so they can be more easily expressed. Often certain base units are set to 1, which makes them dimensionless, at when squared that value does not change. Against these base values such as the amp, or the Kg, different systems of measurement have arisen such as SI or CSG, that we will describe in detail shortly.
Key Ponts
Exact ratio = Exact science
Dimensionless Science correlates scientific formula
Dimensionless Science has defined exact values for over 40 scientific constants. These include further correlations for the Compton wavelength, Hartree energy, and the von Klitzing constant, that can be defined. It also correlates with every equation that formulates the Fine Structure Constant, and offers new insight in its nature.
Constructed from exact ratios
Given this overwhelming level of mathematical precision, we are led to conclude the Universe can be explained through simple ratios that are perfectly described by laws of geometry.
Space is Geometric
The idea that geometry defines the universe is a logic conclusion, when we consider that scientific experimentation is conducted within 3D space. Mathematically, the standard model relies on of vectors, and tensors, that are similarly placed within a co-ordinate system of space.
A Scalable system
Dimensionless Science avoids the need for a fix co-ordinate system, by defining constants as ratios, which are found through simple compass constructions. As such, the system is scalable from the macro to the micro.
4D Perception
Due to this nature, Dimensionless Science can more easily explore the domain of the 4th+ dimensions, which also exhibit the geometric maths of ratio.
Science Without Maths
As ratio can be ascribed to geometry, dimensionless Science offers a unique window into the working of the universe without the need for complicated equations.
History

In the 1920s, Arthur Eddington set out on an extensive investigation of the scientific constants in an attempt to create an overarching mathematical system. However, inaccurate predictions for the value of the fine structure constant created serious problems for his hypothesis. Despite this failure, the enquiry did bring about a recognition of the importance of dimensionless constants, which has since been integrated as a critical aspect of the ‘Standard Model’. Presently, there are around 19 fundamental dimensionless constants describing the masses of the particles and the strengths of the electroweak and strong force, etc.

British theoretical physicist, Michael Duff, who is a pioneer of supergravity, has even suggested that, “varying of dimensional constants is operationally meaningless; variation of dimensionless fundamental “constants” of nature is operationally well-defined and a legitimate subject of physical enquiry.”
Whilst such statements add weight to the importance of a dimensionless approach to science, to date all attempts to produce a convincing model have failed, and currently there are no legitimate contenders who are actively pursuing the idea. Yet if such a system were developed it would undoubtedly have a huge impact on science, and even our very perception of the universe.
I argue that the laws of physics should be independent of one’s choice of units or measuring apparatus. This is the case if they are framed in terms of dimensionless numbers such as the fine structure constant, α. For example, the standard model of particle physics has 19 such dimensionless parameters whose values all observers can agree on, irrespective of what clock, rulers or scales… they use to measure them. Dimensional constants, on the other hand, such as, c, G, e and k …, are merely human constructs whose number and values differ from one choice of units to the next. In this sense, only dimensionless constants are ‘fundamental’. Similarly, the possible time variation of dimensionless fundamental ‘constants’ of nature is operationally well-defined and a legitimate subject of physical enquiry. By contrast, the time variation of dimensional constants such as c or G on which a good many (in my opinion, confusing) papers have been written, is a unit-dependent phenomenon on which different observers might disagree depending on their apparatus. All these confusions disappear if one asks only unit-independent questions. We provide a selection of opposing opinions in the literature and respond accordingly.
Michael Duff
A New system of Science
In 2015, after 2 years of extensively practising the art of compass construction, and an investigation into the regular 3D polyhedra, Colin Power began to recognise that these fundamental forms could be used to express scientific constants and formula. From the seed of an idea, he began to investigate the results of science from the macro to the micro, and discovered the same pattern presents at each scale.
Through his investigation of the Atom, he proposed a new geometric model that defined the spherical harmonics of the electron in simple 3D polyhedra. After constructing a working model, he began to formulate the theory of Atomic Geometry. When he turned his attention to the nature of 4D+ geometry, he found an expression of space that satisfied the criteria for a 4D Aether Theory. He realised that 4D Polyhedra include a component of time, and could also act like an incompressible fluid. From this he was able to conceptualise a 4D Aether theory, however, what was needed was a new kind of mathematics that could describe the 4th dimension, without being tied to the notions of space/time (the meter of the speed of light).
Whilst searching for a solution to this problem, he came across Dimensional Analysis, and realised that it represent the perfect tool to explore scientific constants from the perspective of ratio rather than quantity.
Dimensionless Science is the consequence of this work. This mathematical system can be applied to reality without the need for any kind of man-made axis, as the various ratios express themselves in terms of pure geometry. Spacial orientation is thus defined by the geometry itself, instead of the standard notion that geometry is defined by space.
This idea suggest that the reason for the quantisation of reality is due to the nature of 3D polyhedra, that nest inside one another, to form different shells. It also provides solutions for the ultraviolet catastrophe, and the problem of black body radiation in classical theory. As it is based in the mathematics of ratio, it becomes possible for the student to remember the exact values for large numbers of scientific constants.
Additionally, as complex scientific concepts are presented as tactile geometry that can be constructed, the application of Dimensional Science is suitable for almost all ages. The field of Dimensionless Science is still in inception, however, new discoveries are being made every day that validate it findings. This in turn opens the door for a whole new approach to science, that also reveals some fascinating facts about our universe, and how it is constructed.
Fundamental Constants
When we hear the term Scientific Constant, we might like to think of it as a part of the universe that is fixed in nature. However, constants like The speed of light (c), or the Planck constant (h), are not strictly of this nature as they have associated units. The speed of light is express in meters / seconds. As the relationship of time and space can change due to relativistic effect such as length contraction and time dilation, such units are subject to change.
The notion of fundamental physical constants is often applied to certain universal, but dimensional constants, such as the Planck Constant (h), The speed of light (c), and the Gravitational Constant (G), which are all defined by specified units.
In truth, we should reserve the word fundamental physical constants for those that are not associated with any units. Now, for some the idea of having a scientific constant without units seems rather odd, after all, science is about measuring things, right?
In many cases this might be true, but there are clear exceptions.
Mathematical constants
The most obvious place to find dimensionless constants is mathematics, specifically in the field of geometry. In electromagnetism a Gaussian object is an imaginary shape used to calculate the flux, (amount of energy that moves in and out of a closed system), inside a theoretical closed system. Such techniques employ simple geometric formula to form circles, spheres and other surfaces, which can then be used to help calculate charge.
Every geometric form has its own formula from which it can be created, normally as a ratio of its side-length or radius. For example, we define circles and sphere, etc., using the mathematical ratio π. In mathematics, the notion of π is dimensionless, as it is the expression of a ratio between a circle circumference and its diameter. Another dimensionless geometric constant comes out of the concept of powers, such as 2², which transforms a line (length of 2) into a square divided into 4.
These ratios and mathematical functions are more than a set of linear numbers. They are the transformation of space from one type to another, i.e. from a straight line to a curve, or line to a square. In addition to those mentioned previously, other types of dimensionless values include percentages, and angles. In fact all pure numbers, such as π, e, φ, ½, √2, etc., and units sets of a number, such as the dozen, can be considered dimensionless.
Scientific Constants
Outside the realm of mathematics, there are scientific constants that are dimensionless and universal in nature. Probably the most recognised is the fine structure constant (α). This is not expressed in units of any kind, and yet it is found throughout the universe, from the structure of the atom to the redshift of distant quasars. Due to its widespread appearance, our identification of its exact value in Dimensionless Science sheds new light about its nature.
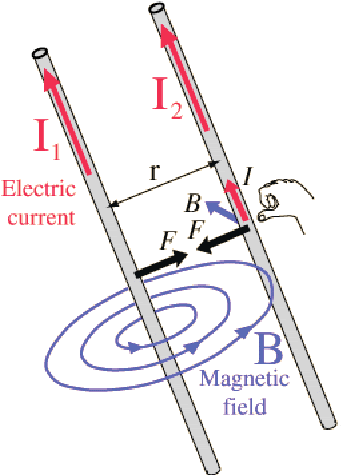
Aside for the fine structure constant, another important constant is the magnetic constant u0. This has traditionally been given the dimensionless value of 4π. This value is derived in the SI unit system through the definition of the Ampere, which considers two infinite parallel wires that carry the same charge. The Amp is defined as the force per unit meter length between the two at a set at distance of 1 meter.
Whilst the SI unit system has been widely adopted, the fields of magnetics is a notable exception, where the general preference is towards the centimetre-gram-second (CGS) system of electromagnetic units (EMU). The key difference is the CGS sets the value of Coulomb’s constant (k) to one, defined by a unit value called electrostatic units (ESU). In this way, the Coulomb’s constant becomes dimensionless. Often when converting between Coulombs and ESU the numerical difference is absorbed by the factor c, the speed of light.
1 Coulomb (k) x Speed of Light = 1 Electrostatic Unit (ESU)
Mass constants
The Third type of Universal scientific constants appear as the experimental mass values of fundamental particles, such as electrons, protons, and neutrons. Presently, there is no concise theory to explain why these masses should be the set at their specific values. This standard model of science has defined values for a plethora of fundamental particles including Quarks, Lepton’s, and Bosons.
These mass values have been ascertained in the main through experiments with particle colliders. However, it is worth pointing out that the majority of the mass of these particles come from their energetic interactions. For example, Protons and Neutrons are made up of a group of three quarks.
Traditional Measurement Systems
In a drastic redesign of the SI system on 20 May 2019, the International Committee for Weights and Measures (CIPM) altered the nature u0 changing it from a dimensionless constant to a value that now needs to be determined experimentally. This move came about through a decision to try and focus measurement standards upon the newly fixed Planck constant.
In the CGS system, the magnetic and electric fields in a vacuum are equal in value and dimension, despite their different units. Whereas, in the SI system, these fields are converted through the fixed constant μ0 with a value of 4π, as they have different values and dimensions. The consequence of this recent shift is a departure from such a simple convention, and away from the idea of dimensionless science.
Dimensionless Science
The Process
Whilst the current trend in science is to seek more and more accurate definitions of constants through experimental results, Dimensionless Science goes in the opposite direction. Instead, it seeks to examine the relationship of various equations, and find a system of coherence in geometric terms. The ratios are developed without consideration of scale, which is analysed once the geometric concepts have been established. Therefore, we can say that the process of investigation follow three simple steps.
1
Perform the calculation using dimensionless science constants
2
Assertain a geometric value for the new constant
3
Adjust the calculation if needed to output the correct magnitude
In Dimensionless Science, we sometimes consider objects in a higher dimension than 3D. As higher dimensional objects cannot be measured in a 3D reality, they are best explored in a dimensionless context first, and then appropriated to our 3D reality subsequently.
Powers and Dimensions
There are certain numbers that do not translate well onto a standard calculator, without fully understanding the limitations of linear sums. For example, if we take the number one and square it (1²), the answer on a calculator will be one. Cube it (1³) and the result is still one. In fact, the number one can take to any power without changing its apparent value. It is dimensionless. However, I can draw a line (1), and make a square from it (1²), and then I can draw a cube (1³).
Therefore we can see that numbers can be deceiving, and so when we endeavourer to make sense out of a dimensionless system of scientific constants, the geometry of the concept must also be deeply considered.
Ratios
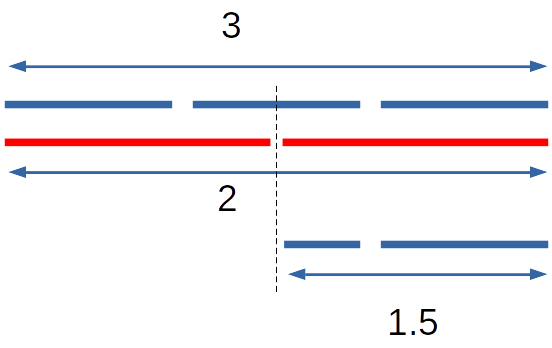
Another clear example how numbers can be deceiving is found in the nature of ratios. In fact, there are many different kinds of ratio, the simplest being a fraction made of two whole numbers. Geometrically, a fraction can be seen as a line length of a certain number of units whose total length is divided. For example, the fraction 3/2 is a line of unit length 3, divided in half.
When we add another term to the fraction, we create a three term ratio. These are different in nature as they have certain are predictive qualities. They can grow or shrink in size at a defined rate. For example, the fraction 3 : 9 can also be written as 1 : 3. However, when we add another term to the start we define a different perspective, dependent on the value added. For example:
1 : 3 : 9 or √3 : 3 : 9
Dimensionless Axis
One of the reason many people believe that the humans are unable to model the universe, is the fact that all scientific measurement has to have some kind of axis in order to define reality. From the simple number line to flattened Minkowski space-time, one thing all scientific investigation employs is some kind of mathematical space that is governed by co-ordinate sets of numbers. It is recognised that if the axis is moved or rotated, then the outcome values will also change. This video from Numberphile explains the problem in more detail.
In effect, the universe does not care about up or down, neither does it take measurements each time it performs and action. It is humans who construct the framework of space with units through which our investigations are metered. So how can we get away from this nature.
Dimensionless Science employs the art of compass construction that requires no measurement in order to define specific geometric relationships. Just as everything is relative in the universe, so the same can be said of compass construction.
In this example, we can move the two dots at the centre of each circle into any orientation and any distance, and the overall images remains intact.
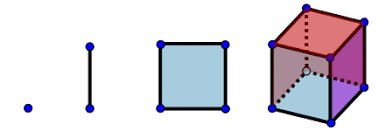
The only factor that defines the scale of any particular form is the initial opening of the drawing compass. This we make dimensionless by setting its value to ONE. In addition to not requiring any kind of axis or scale, the results are embedded into simple images that we believe make understanding and remembering scientific concepts a far easier task. Through a hands-on approach, we can move from the 2nd dimension and into the 3rd by building various polyhedra and nesting them with specific ratios. We have found that from this perspective, people find it far easier to comprehend the 4th and higher dimensions.
Based on our experience, we have developed our 4D thinking and 5D thinking programs that are aimed at improving our mental ability to visual geometrically. The universe becomes easier to comprehend through geometric thinking, from which dimensionless science expands into the arena of scientific reasoning.
THE
Conclusion
Dimensionless Science transforms our traditional scientific notation into easy to understand geometric examples, by translating various universal constants into geometric ratios.
It produces coherent results that are close to traditional scientific notation.
It is far easier to comprehend
It lends itself to geometric scientific model
It opens the door for a new theoretical perspective based on the geometric nature of the universe.