Create the 5 Platonic Solids
Only 5 regular solids in 3D
Just as 2D space is limited to only 2 types of regular 2D tessellation that can fill a plane with just two colours, there are only five regular solids. These Platonic Solids have the characteristic of being formed from the same equal-sided shapes. Three of these, the tetrahedron, octahedron, and icosahedron have triangular faces, whilst the cube has square faces, and the dodecahedron pentagonal.

Tetrahedron
The Tetrahedron is the simplest of the Platonic solids. It is made up of the same number of faces and corners, i.e. four equilateral triangles and four vertices. It is the only one, which can be placed with one triangular face on a flat surface to form a pointed pyramid, while all others are flat.

Octahedron
The octahedron is made up of eight equilateral triangles and has six vertices and twelve edges. It can be seen as two square-based pyramids stacked together.

Hexahedron (cube)
The cube, also known as the hexahedron, is one of the most familiar of the Platonic solids. It is made up of six square faces, twelve edges, and eight vertices.

Dodecahedron
The dodecahedron is a complex shape made up of twelve regular pentagons. It has twenty vertices and thirty edges. It is the only one based on a pentagon, which naturally embodies the Golden Ratio.

Icosahedron
The Icosahedron is made up of twenty equilateral triangles and has twelve vertices and thirty edges. Just as the Tetrahedron and Octahedron, it is also based on triangular faces. Yet, it is the only Platonic Solid which can create a central pentagon prism.
Describing the 5 Platonic Solids
Each Platonic Solid is based on a particular number of three different polygons, the triangle (3), square (4) and pentagon (5). To describe how many faces and which type of faces are meeting at each vertex, a certain writing has been introduced. In terms of the Tetrahedron, we have three triangles meeting at each vertex, denoted as 33. For the Octahedron, three squares meet at a vertex, denoted as 34, and so on. in the following table, you can see an overview of the number of faces, the properties of each vertex, number of vertices and edges describe each solid.
|
Platonic Solid
|
Faces
|
Face Type
|
Vertices
|
Edges
|
|---|---|---|---|---|
|
Tetrahedron
|
4
|
Triangle
|
4
|
6
|
|
Octahedron
|
8
|
Triangle
|
6
|
12
|
|
Cube
|
6
|
Sqaure
|
8
|
12
|
|
Dodecahedron
|
12
|
Pentagon
|
20
|
30
|
|
Icosahedron
|
20
|
Triangle
|
12
|
30
|
Creating the Archimedean SOlids
From 5 Platonic Solids another set of semi-regular polyhedra, called the 13 Archimedean Solids, can be derived. Aside from the Truncated Tetrahedron, the other 12 fall into two distinct categories. Some are based on the Octahedron and Cube with octahedral symmetry, and another six are derived from the Dodecahedron and Icosahedron, that exhibit icosahedral symmetry.
|
Archimedean Solid
|
Faces
|
Face Type
|
Vertices
|
Edges
|
|---|---|---|---|---|
|
Truncated Tetrahedron
|
4 / 4
|
Trinagle / Hexagon
|
12
|
24
|
|
Cuboctahedron
|
8 / 6
|
Triangle / Sqaure
|
12
|
18
|
|
Truncated Cube
|
8 / 6
|
Trinagle / Octagon
|
24
|
36
|
|
Truncated Octahedron
|
6 / 8
|
Square / Hexagon
|
24
|
36
|
|
Rhombicuboctahedron
|
8 / 18
|
Triangle / Square
|
24
|
48
|
|
Snub cube
|
32 / 6
|
Triangle / Sqaure
|
24
|
60
|
|
Great Rhombicuboctahedron
|
12 / 8 / 6
|
Square / Hexagon / Octagon
|
48
|
72
|
|
Icosidodecahedron
|
20 / 12
|
Triangle / Pentagon
|
30
|
60
|
|
Truncated Dodecahedron
|
20 / 12
|
Triangle / Pentagon
|
60
|
90
|
|
Truncated Icosahedron
|
12 / 20
|
Pentagon / Hexagon
|
60
|
90
|
|
Rhombicosidodecahedron
|
20 / 30 / 12
|
Triangle / Square / Pentagon
|
60
|
120
|
|
Great Rhombicosidodecahedron
|
30 / 20 / 12
|
Sqaure / Hexagon / Decagon
|
120
|
180
|
|
Snub Dodecahedron
|
80 / 12
|
Triangle / Pentagon
|
60
|
150
|
Three Geometric Processes
The 13 Archimedean Solids are produced from the 5 Platonic Solids through three geometric processes: truncation, explosion and twisting.
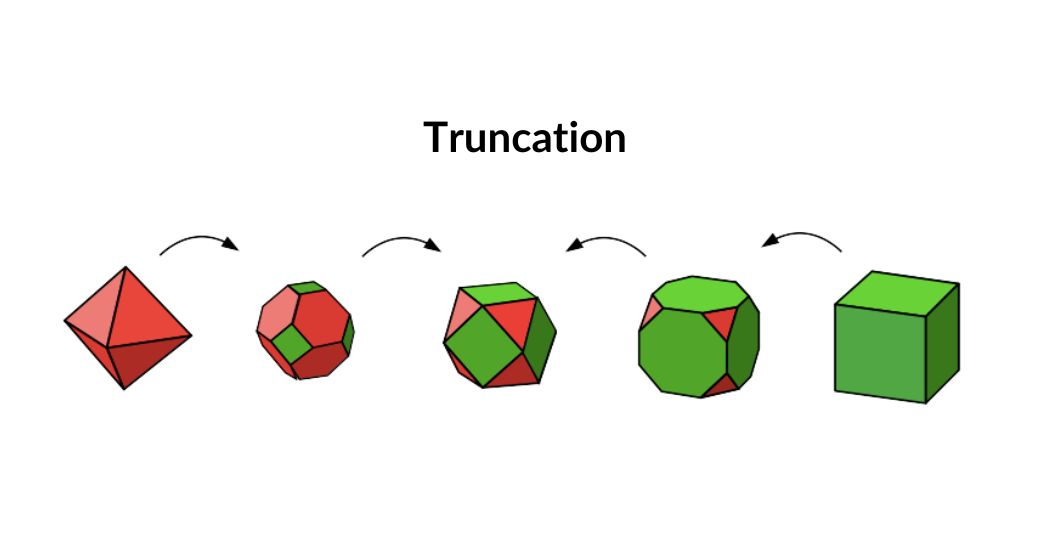
Truncation
Each side can be divided into two or three and the corner parts removed. Truncating a solid reduces its volume, i.e. makes it smaller. Solids that can be created through truncation include, the Cuboctahedron, the Truncated Cube and the Truncated Octahedron, all of which are used in the construction of the Atomic geometry.
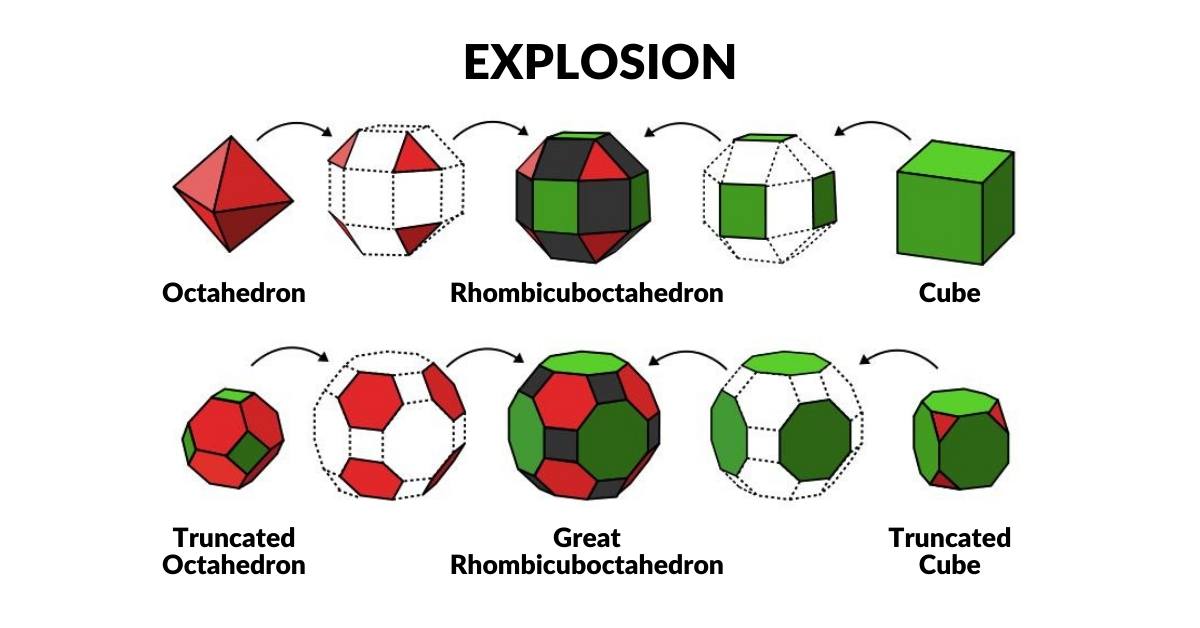
Explosion
By moving the faces of a solid away from its centre until the spaces between each face can be filled with other regular shapes, we create an exploded solid. Examples of this include, The Rhomicuboctahedron, and the Great Rhombicuboctahedron, both of which appear in Atomic geometry.
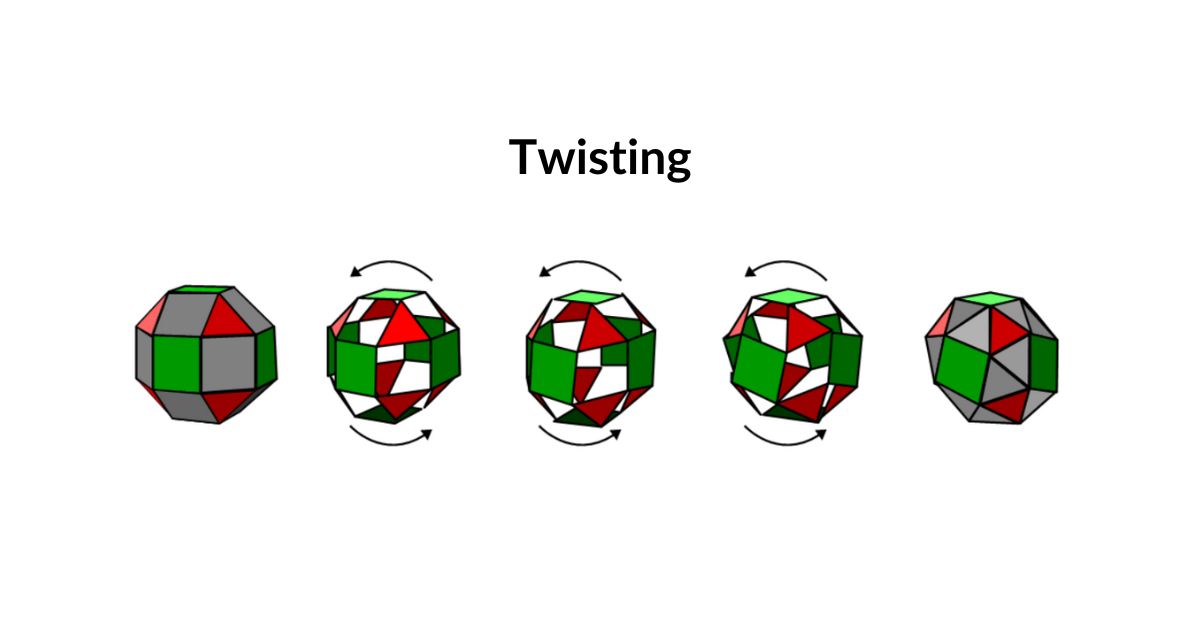
Twisting
A square can transform into two triangular faces when it is twisted into a parallelogram. In this way, the Rhombicuboctahedron can be transformed into a snub cube. Twisting differs from the other two processes as it is chiral, meaning it can occur in a left or right orientation.
Not only have we discovered that the sub-orbitals occupy spaces that can be defined by these polyhedra, we also suggest that it is these three geometric principles that are at work, transferring the energy of the electron instantaneously between shells. This creates the quantisation effects found at the atomic scale.

The 5 Elements Course
A Journey into 3D
Construct the 5 Platonic Solids in 2D and 3D and discover their novel relationship to the 5 Elements



